Analyse de l'évolution des recettes de services issues des secteurs Education et Santé au Cameroun de 2003 à 2008 et prévisions à court terme

§. 3- Modélisation du processus générateur de la série Yt

Ici, nous allons dérouler les différentes étapes de la méthode de Box et Jenkins.

2. Recherche de la représentation adéquate : l'identification

L'analyse des corrélogrammes simple et partiel de la série (voir graphique 14 en annexes) ne permet pas d'identifier clairement un processus AR ou MA. En effet, les estimations de la fonction d'autocorrélation et de la fonction d'autocorrélation partielle observées, ne sont pas typiques de ces processus. De ce fait, nous pencherons pour un processus de type ARMA et les modèles candidats sont alors ARMA(1,1), ARMA(1,2), ARMA(2,1) et ARMA(2,2).

2. Estimation des paramètres des modèles candidats

L'estimation des paramètres des quatre modèles candidats, donne les résultats consignés dans le tableau ci-dessous :

Tableau 3: Estimation des paramètres des différents modèles ARMA

Modèles	Paramètres	Estimations	Ecart-types	t	p-valeur
ARMA (1,1)	AR1	-0,7896	0,1314	-6,0086	0,0000
	MA1	-0,9914	0,3111	-3,1864	0,0022
	CONSTANTE	1,0005	0,0080	124,6562	0,0000
ARMA (2,1)	AR1	-0,7061	0,1591	-4,4371	0,0000
	AR2	0,1076	0,1361	0,7907	0,4319
	MA1	-0,9737	0,1558	-6,2499	0,0000
	CONSTANTE	1,0007	0,0090	111,2478	0,0000
ARMA (1,2)	AR1	-0,8515	0,1680	-5,0673	0,0000
	MA1	-1,1149	0,9774	-1,1407	0,2580
	MA2	-0,1176	0,2176	-0,5407	0,5905
	CONSTANTE	1,0006	0,0087	114,7580	0,0000
ARMA (2,2)	AR1	0,7576	0,3933	1,9263	0,0583
	AR2	0,0366	0,3847	0,0951	0,9245
	MA1	0,6118	1,0743	0,5695	0,5709
	MA2	0,3838	0,6337	0,6057	0,5468
	CONSTANTE	0,9999	0,0019	515,9267	0,0000

A la lecture de ce tableau, on remarque que seul le modèle ARMA(1,1) a tous ses paramètres qui sont significativement différents de zéro au niveau =5% (on a des p-valeurs qui sont toutes inférieures à 0,05). Ainsi donc, la représentation ARMA (1,1) semble être le plus adéquate pour modéliser le processus générateur de la série Y_t, sous réserve de la validation des hypothèses sur les résidus.

3. Validation du modèle ARMA(1,1) retenu

a) Analyse graphique

Comme on peut le voir sur le graphique 9 ci-après, les résidus du modèle ARMA(1,1) retenu se comportent comme un bruit blanc. En effet, ces résidus fluctuent autour d'un niveau moyen égal à zéro. En outre, dans les corrélogrammes simple et partiel (voir graphique 15 en annexes), on observe que les estimations de la fonction d'autocorrélation et de la fonction d'autocorrélation partielle sont toutes dans l'intervalle de confiance (c'est-à-dire que les coefficients correspondants ne sont pas significativement différents de zéro). Compte tenu de ces résultats, nous sommes portés à admettre que les résidus sont bien bruit blanc et donc, que le modèle retenu est valide.

Graphique 9: Résidus du modèle ARMA(1,1)

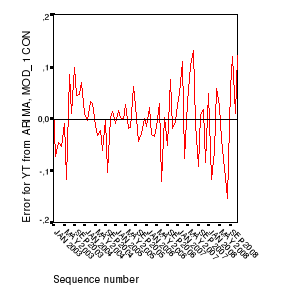
Nous allons renforcer cette conclusion de validité du modèle retenu en effectuant les tests requis sur les résidus.

b) Tests sur les résidus

Ø Hypothèse de nullité de l'espérance des erreurs

La valeur observée de la statistique de test est donnée par : 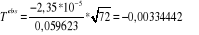. La valeur critique de loi de Student à 71 dégrés de liberté pour = 5% vaut T=1,993943. On constate que la valeur observée de la statistique de test est inférieure en valeur absolue à la valeur critique de la loi de Student ( |T^obs| < T ), ceci conduit au non rejet de l'hypothèse principale H₀ qui stipule que l'espérance des résidus est nulle.

Ø Hypothèse de non autocorrélation des résidus

Les statistiques de Ljung-Box (Q-stat) sont toutes non significatives au seuil de 5%, comme on peut le voir dans le graphique 15 en annexes ; en effet, elles sont toutes supérieures à 0,05. Ceci nous permet de valider l'hypothèse nulle de non autocorrélation des résidus.

Ø Hypothèse d'homoscédasticité des résidus

Pour valider cette hypothèse, nous allons utiliser le test ARCH de Engel. Ce test effectué avec le logiciel Eviews et dont le résultat figure dans l'encadré 1 ci-dessous, est non significatif au seuil =5%. En effet, on a p-valeur = 0,403885 > 0,05. Ceci conduit au non rejet de l'hypothèse principale d'homoscédasticité des résidus.

Encadré 1: Résultat du test ARCH de Engel

Ø Hypothèse de normalité des résidus

Ici, nous utiliserons le test de Jarque-Bera, dont l'hypothèse principale H₀ postule que les résidus suivent une loi normale. Le résultat de ce test, présenté dans l'encadré 2 ci-après, montre que la statistique de test est non significative au seuil de 5%. On a en effet une p-valeur de 0,948611 qui est supérieure à 0,05. On ne rejette donc pas H₀, ce qui signifie que l'hypothèse de normalité des résidus est bien valide pour le modèle retenu.

Encadré 2: Résultat du test de Jarque-Bera de normalité des résidus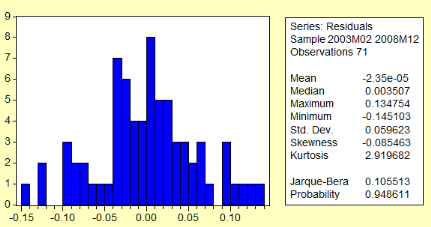

Puisque les résidus du modèle retenu vérifient toutes les hypothèses requises, nous pouvons considérer que ledit modèle est correct. Ainsi donc, l'équation de prédiction de la série des recettes du secteur santé corrigée des variations saisonnières et débarrassée de la tendance déterministe, s'écrit comme suit :

.
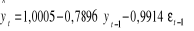