Analyse de l'évolution des recettes de services issues des secteurs Education et Santé au Cameroun de 2003 à 2008 et prévisions à court terme

§.2- Etude de la stationnarité de la chronique

1. Analyse graphique

Etant donné que nous avons détecté une composante tendance déterministe dans la série des recettes du secteur santé, nous allons préalablement enlever cette tendance de la série corrigée des variations saisonnières. Soit donc la nouvelle série Y_t définie par :

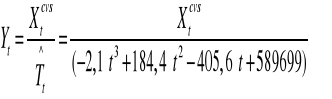
Elle fluctue autour de sa moyenne comme on peut le voir sur le graphique 11 ci-dessous, ce qui laisse croire que cette série est stationnaire.

Graphique 7: Série corrigée des variations saisonnières et débarrassée de la tendance déterministe

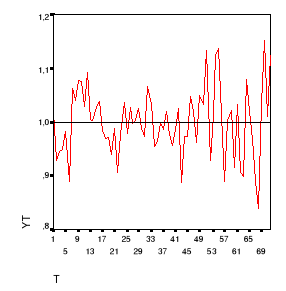
Source : DPB

Ce résultat semble se confirmer par l'examen du corrélogramme simple de la série Y_t (voir graphique 18 en annexes) qui ne présente pas une décroissance lente et dans lequel les estimations de la fonction d'autocorrélation oscillent autour de zéro malgré la présence de deux barres qui touchent les limites de l'intervalle de confiance.

Pour confirmer la stationnarité de la série Y_t, nous allons procéder au test de la racine unitaire de Dickey-Fuller.

2. Test de la racine unitaire de Dickey-Fuller

a) Détermination du nombre de retard optimal pour la réalisation du test

L'application de la stratégie de test de Dickey-Fuller augmenté nécessite la recherche du nombre de retard optimal qui permet de « blanchir » les résidus.

· Analyse de la fonction d'autocorrélation partielle de Y_t

Dans le graphique ci-dessous, on peut voir que la dernière autocorrélation partielle de Y_t qui est significativement différente de zéro, est observée pour p=4.

Graphique 8: Corrélogrammes simples et partiels de la série différenciée Yt

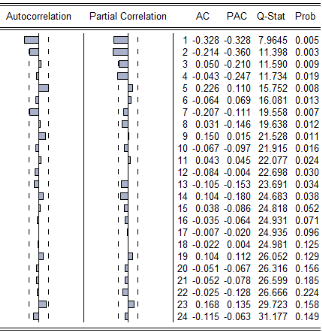
Nous allons donc analyser les critères d'information pour p allant de 0 à 4.

· Minimisation des critères d'information

Nous allons estimer chacun des trois modèles présentés au chapitre précédent pour un nombre de retard allant de 0 à 4, puis nous retiendrons celui qui minimise les critères d'information AIC et SBIC.

Les résultats obtenus sont consignés dans le tableau suivant :

Tableau 2: Détermination du nombre de retard optimal pour le test de la racine unitaire

p	Modèle 3		Modèle 2		Modèle 1
	AIC	SBIC	AIC	SBIC	AIC	SBIC
0	-2,212138	-2,180269	-2,668359	-2,604621	-2,642413	-2,546807
1	-2,306351	-2,242108	-2,654355	-2,557990	-2,626073	-2,497587
2	-2,408672	-2,311537	-2,618079	-2,488565	-2,589097	-2,427205
3	-2,413329	-2,282769	-2,581759	-2,418560	-2,552774	-2,356935
4	-2,464115	-2,299586	-2,559423	-2,361988	-2,530218	-2,299877

Il ressort de ce tableau que le nombre de retard optimal pour la réalisation du test ADF est p=0.

b) Test de Dickey-Fuller augmenté

Le test ADF pour le modèle général (modèle 1) avec tendance et constante conduit au rejet de l'hypothèse nulle de non stationnarité DS (ou encore de présence d'une racine unitaire). En effet, la valeur de la statistique de test (-6,513253) est inférieure à la valeur critique tabulée de Dickey-Fuller (quel que soit le seuil) : -4,092547 (1%); -3,474363 (5%) et -3,164499 (10%) (voir encadré 8 en annexes). Puisque le processus n'est pas DS, on va voir s'il est TS. Pour cela, on teste l'hypothèse H₀' : b=0 avec le seuil de la loi normale. En ce référant à l'encadré 8 en annexes, on voit que la statistique de test t_b vaut 0,389052 et est inférieure en valeur absolue à la valeur critique de la loi normale au seuil de 5% (1,96). On ne rejette donc pas H₀' et par conséquent, le modèle 1 n'est pas le « bon » modèle ; on passe au modèle 2.

L'estimation du modèle 2 avec constante et sans tendance conduit au rejet de l'hypothèse principale H₀ de présence d'une racine unitaire. Dans l'encadré 9 en annexes, on a en effet la statistique de test t qui vaut -6,558244 et est inférieure aux valeurs critiques de Dickey-Fuller pour différents seuils : -3,525618 (1%) ; -2,902953 (5%) et -2,588902 (10%). On teste ensuite l'hypothèse H₀'' : c=0 en utilisant la valeur critique de la loi normale. Le résultat (voir encadré 9 en annexes) indique que la statistique de test t_c (6,557415) est supérieure en valeur absolue à 1,96 ; on rejette donc H₀''. Ainsi, le processus générateur de la série y_t est de la forme Y_t = c + _t ; c'est donc un processus stationnaire puisqu'il s'écrit comme étant une constante plus une perturbation aléatoire.

En conclusion, l'analyse graphique et le test de Dickey-Fuller augmenté nous permettent d'être en faveur de l'hypothèse de stationnarité du processus générateur de la série corrigée des variations saisonnières et débarrassée de la tendance déterministe.