Chapitre 2
Application de l'algorithme
d'optimisation par essaims
particulaires aux problèmes MSAP
et PAF
2.1 Introduction
La résolution d'un problème d'optimisation
consiste à explorer un espace de recherche afin de maximiser (ou
minimiser) une fonction objectif. En effet, dans la vie courante nous sommes
fréquemment confrontés à des problèmes réels
d'optimisation plus ou moins complexes.
En général, deux sortes de problèmes
reçoivent, dans la littérature, cette appellation :
Certains problèmes d'optimisation discrets, pour lesquels
on ne connait pas d'algorithme exact polynomial (NP-difficiles),
Certains problèmes d'optimisation à variables
continues, pour lesquels on ne connait pas d'algorithme permettant de
repérer un optimum global à coup sûr et en un nombre fini
de calculs.
Des efforts ont été longtemps menés,
séparément, pour résoudre ces deux types de
problèmes. Dans le domaine de l'optimisation continue, il existe un
arsenal de méthodes classiques, mais ces techniques se trouvent souvent
limitées. Cette limitation est due soit à l'absence de
modèles analytiques, soit à l'inadéquation des techniques
de résolution. Dans le domaine de l'optimisation discrète, un
grand nombre d'heuristiques, qui produisent des solutions proches de l'optimum,
ont été développées, mais la plupart d'entre elles
ont été conçues spécifiquement pour un
problème donné.
L'arrivée des métaheuristiques marque une
réconciliation des deux domaines : en effet, celles-ci s'appliquent
à toutes sortes de problèmes discrèts et elles peuvent
s'adapter aussi aux problèmes continus.
L'algorithme d'optimisation par essaims particulaires (PSO)
fait partie de ces métaheuristiques. cet algorithme est basé sur
la notion de coopération entre des agents (les particules qui peuvent
être vues comme des « animaux » aux capacités assez
limitées : peu de mémoire et de facultés de raisonnement).
L'échange d'information entre les agents fait que, globalement, ils
arrivent néanmoins à résoudre des problèmes
difficiles voire complexes.
Dans ce chapitre, l'algorithme d'optimisation par essaims
particulaires est implémenté pour résoudre deux
problèmes réels, un problème continu : la commande d'une
machine synchrone à aimant permanent, et un autre discret : le
problème d'affectation de fréquences dans les réseaux
cellulaires.
2.2 Commande en vitesse des machines synchrones
à aimant permanent (MSAP)
Les machines synchrones à aimant permanent (MSAP) sont
de grand intérêt, particulièrement dans les applications
industrielles de faible et moyenne puissance, puisqu'elles possèdent de
bonnes caractéristiques telles que la compacité de la dimension,
bons rapports couple/poids et couple/inertie et l'absence des pertes dans le
rotor [Slemon, 1994]. Cependant, la performance de MSAP est très
sensible aux variations de paramètres et aux perturbations externes de
charge dans le système.
La conception du contrôleur conventionnel, i.e.,
Proportionnel-Intégrateur (PI), est basée sur un modèle
mathématique du dispositif utilisé, qui peut souvent être
inconnu, non-linéaire, complexe et multi-variable avec variation de
paramètres. De ce fait, le contrôleur conventionnel PI ne
présente pas, en général, une solution utile pour la
commande du moteur MSAP. Pour surmonter ces problèmes, plusieurs
stratégies de commande ont été proposées pour la
commande en vitesse des MSAP, notamment par : la logique floue [Lee, 1990],
[Akcayol et al, 2002], les réseaux de neurones artificiels [Lin et Lee,
1991] [Rahman et Hoque, 1998], les algorithmes génétiques
[Loukdache et al, 2007], et par les essaims particulaires [Benameur et al,
2007].
Dans les sections suivantes nous décrivons la
modélisation des MSAP, nous présentons les résultats de
simulation relatifs à l'utilisation d'un PI basé sur les essaims
particulaires (PIPSO) [Benameur et al, 2007] et nous comparons enfin les
résultats avec ceux obtenus par l'utilisation des algorithmes
génétiques (PIGA) [Loukdache et al, 2007].
2.2.1 Modélisation d'une machine synchrone à
aimant permanent
La configuration du système de commande des MSAP est
donnée par la figure (2.1). Le système de commande se compose
d'un contrôleur de vitesse, d'un régulateur de courant, d'un
contrôleur de courant à bande d'hystérésis, d'un
onduleur triphasé et d'un capteur de position.
èr représente la position du
rotor, wr est la vitesse actuelle, i* a,
i* b, i* c, sont les courants de phase de
référence et ew désigne l'erreur en
vitesse. ew est la différence entre la vitesse de
référence w* r et la vitesse actuelle
wr. Utilisant l'erreur en vitesse ew,
le contrôleur de vitesse génère un courant appelé
courant de référence ou courant de contrôle
I*.
La figure (2.2) illustre le circuit équivalent de MSAP et
de l'onduleur triphasé.
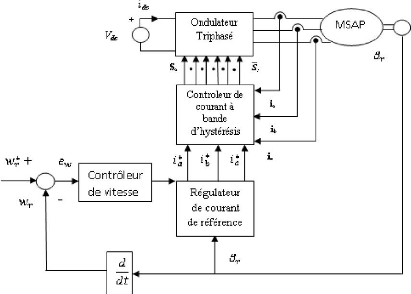
FIG. 2.1 - Schéma de la commande en vitesse de MSAP
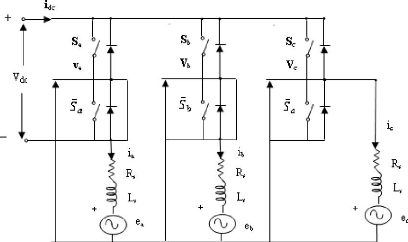
FIG. 2.2 Circuit équivalent de MSAP et de l'onduleur
triphasé
Les équations de tension au niveau du stator de la MSAP
sous forme matricielle sont données par l'équation (2.1).
?
?
Va
Vb
Vc
? ? ? ? ? ? ? ? ? ? ?
Rs 0 0 ia Ls
0 0 ia ea
d
? = ? 0 Rs 0 ? ? ib ? ? 0
Ls 0 ? ? ib ? + ? eb ? (2.1)
0 0 Rs ic 0 0 Ls dt
ic ec
Les équations d'état associées à
l'équation (3.1) peuvent être écrites selon la formule
(2.2) :
d I ia 1 = I L0 s
L0 0 1-1 {[ s 1[ 1 -- [
-Rs 0 0 ia ea Va 1
0 -R 0 ib eb 1 [ V } (2.2)
dt I_ ic j I_ 0 0
Ls i 0 0 -Rs ic ec #177;
Vcb
La vitesse du rotor et le couple électrique
Te peuvent être formulés selon les
équations (2.3) et (2.4) :
|
d
dtùr =
|
p2 (Te -- TL -- B
(2) ùr) /J (2.3)
p
|
Te = K I* (2.4)
Où K = -4
3p ëf et ëf est le flux dû
à l'aimant permanent du rotor. L'équation du contrôleur de
courant de bande d'hystérésis est donnée par
l'équation (2.5).
(
hx = 1 si i*-- ix
< 0.5hrb
(2.5)
0 si i* x-- ix >
--0.5hrb
Où, x représente a, b, c respectivement.
hx désigne la fonction du contrôleur de courant
à bande d'hystérésis ha, hb,
hc. hrb est le rang du contrôleur de
courant à bande d'hystérésis. En utilisant la fonction
hx, l'équation (2.2) peut être formulée de
la façon donnée en équation (2.6) :
[ ia i i
0 0 Ls 0 0 --Rs
ec
ib = [ 0 L 0
Ls s 0 -1 [ 0
--Rs
--Rs 01 [ib-- [
ee:+ (-ha+2hb-hcgb
)
(-ha --F2hc)
d
dt
(2ha
[vdc]

3
(2.6)
| 


