3.6.2 Résultats numériques
Les paramètres u et u,
utilisés dans l'équation de la mise à jour du vecteur
vitesse (équation (1.1)), sont initialisés à 1.02
pour toutes les fonctions tests, ô(t) varie
linéairement de 0.7 à 0.2 pendant les
différentes itérations. Le modèle est appliqué
à un essaim de 80 particules pour les fonctions F1,
F2, F3, F4 et F5. Pour la fonction F6,
la taille de l'essaim est 100. Des différentes tailles de l'essaim sont
testées pour détecter les optimums de la fonction F7 et
les meilleurs résultats sont trouvés pour un essaim de 400
particules.
Fonction F1
Le modèle converge à la quatrième
itération. Le tableau (3.1) représente l'évolution de
l'entropie h et le nombre de classes détectées (C)
à la première itération pour différents seuils de
similarité. La meilleure partition correspond à la plus petite
valeur de l'entropie.
Comme le montre le tableau (3.1), la valeur 50.6% de
similarité fournit la meilleur partition (C = 5) qui correspond
à la plus petite valeur d'entropie (h = 4.11E
--02).
Le tableau (3.2) montre l'évolution des optima
détectés, il faut noter que les centres des classes sont
définis par leurs coordonnés et leurs fitness, C
représente le nombre de classes identifiées.
TAB. 3.1 - Evolution de la valeur d'entropie et du nombre de
classes pour les différentes valeurs de similarité
|
Smin(%)
|
C
|
h
|
|
31.6
|
2
|
0.417
|
|
40.6
|
3
|
0.392
|
|
50.6
|
5
|
4.11E-02
|
|
57.6
|
6
|
6.67E-02
|
|
60.6
|
7
|
4.14E-02
|
|
64.6
|
8
|
6.03E-02
|
|
67.6
|
10
|
0.138
|
TAB. 3.2 - Evolution de la valeur d'entropie, des centres et des
rayons de classes de la fonction F1.
|
1erCycle(C = 5)
|
2èmeCycle(C = 5)
|
3èmeCycle(C = 5)
|
4èmeCycle(C = 5)
|
|
Centre Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
|
(0.097, 0.917)
|
0.037
|
(0.101,0.985)
|
0.009
|
(0.1, 0.999)
|
0.0016
|
(0.1,1)
|
0
|
|
(0.301,0.961)
|
0.038
|
(0.299,0.989)
|
0.016
|
(0.3, 0.998)
|
0.004
|
(0.3,1)
|
0
|
|
(0.501,0.982)
|
0.010
|
(0.500,0.999)
|
0.002
|
(0.5,1)
|
0
|
(0.5,1)
|
0
|
|
(0.697, 0.955)
|
0.073
|
(0.699, 0.94)
|
0.019
|
(0.7, 0.997)
|
0.005
|
(0.7,1)
|
0
|
|
(0.899,0.953)
|
0.027
|
(0.899,0.992)
|
0.006
|
(0.9,0.999)
|
0.003
|
(0.9,1)
|
0
|
|
h
|
0.041
|
|
0.010
|
|
0.002
|
|
3E-06
|
|
MRP
|
0.954
|
|
0.981
|
|
0.999
|
|
1
|
L'analyse de ces résultats montre que les cinq classes
détectées, au premier cycle, ne sont pas chevauchée et
chaque classe contient un seul optimum. Même si les cinq optima ont
été trouvés au premier cycle, les cycles suivants du
processus permettent un ajustement local fin de ces optima, cet effet tend
évidemment à améliorer la qualité des solutions.
Ceci est confirmé par la valeur de MRP, qui vaut 0.954 au premier cycle
et 1 au dernier.
La figure (3.4) représente la distribution des particules
dans l'espace de recherche durant chaque cycle du processus
d'évolution.
Fonction F2
Les résultats de simulation obtenus sont
présentés dans le tableau (3.3).
TAB. 3.3 - Evolution de la valeur d'entropie, des centres et des
rayons de classes de la fonction F2.
|
1erCycle(C = 6)
|
2èmeCycle(C = 5)
|
3èmeCycle(C = 5)
|
4èmeCycle(C = 5)
|
|
Centre
|
Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
|
(0.144,0.122)
|
0.009
|
(0.104,0.939)
|
0.028
|
(0.101,0.988)
|
0.008
|
(0.1,1)
|
0
|
|
(0.298,0.889)
|
0.019
|
(0.298,0.913)
|
0.006
|
(0.299,0.916)
|
0.002
|
(0.3,0.917)
|
0
|
|
(0.499,0.678)
|
0.054
|
(0.499,0.691)
|
0.014
|
(0.499,0.707)
|
0.003
|
(0.5,0.707)
|
0
|
|
(0.698,0.440)
|
0.031
|
(0.698,0.457)
|
0.006
|
(0.698,0.459)
|
0.002
|
(0.7,0.459)
|
0
|
|
(0.962,0.942)
|
0.067
|
(0.897,0.251)
|
0.002
|
(0.9,0.25)
|
0
|
(0.9,0.250)
|
0
|
|
(0.897,0.241)
|
0.013
|
-
|
|
-
|
|
-
|
|
|
h
|
0.076
|
|
0.014
|
|
2.7 E-06
|
|
1E-05
|
L'analyse des classes et des rayons montre que la
cinquième et la dernière classe sont chevauchées, et
toutes les deux contient le même optimum au point x =
0.9.
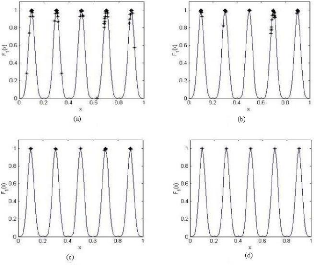
FIG. 3.4 - Placement des individus dans l'espace de recherche
durant l'évolution de MPSO pour la fonction F1
Ces deux classes se recouvrent et forment une classe unique
à l'itération suivante. A ce stade, même si les cinq optima
sont déjà identifiés, la valeur d'entropie continue
à diminuer, l'algorithme converge au quatrième cycle (h
= 1E - 05). Dans ce cas, toutes les particules de même
sous-essaim sont identiques et ont la même fitness (figure 3.5), ce qui
correspond à un rayon de classe égal à zéro.
Fonction F3
Pour cette fonction, l'algorithme converge à la
troisième itération et tous les optima sont localisés. La
valeur d'entropie à la convergence du processus est égale
à 6.9E - 04.
La distribution des particules dans l'espace de recherche durant
chaque cycle du processus d'évolution est représentée dans
la figure (3.6).
A la première itération, les particules sont
aléatoirement placées dans l'espace de recherche. Ces particules
se regroupent progressivement autour du plus proche pic. A la convergence de
l'algorithme, toutes les particules de même sous-essaim sont identiques
et ont la même fitness.
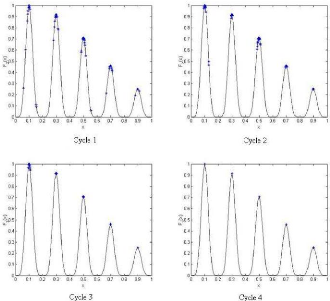
FIG. 3.5 - Distribution des individus dans l'espace de recherche
durant l'évolution de MPSO pour la fonction F2
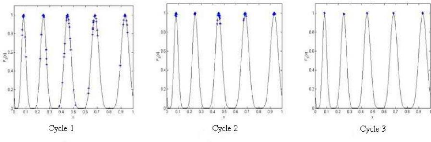
FIG. 3.6 Placement des individus dans l'espace de recherche
durant l'évolution de MPSO pour la fonction F3
Fonction F4
Le processus converge à la quatrième
itération quand la valeur d'entropie est égale à
9.82E - 04. La figure (3.7) représente la distribution
des particules dans l'espace de recherche durant l'évolution de MPSO
pour la fonction F4.
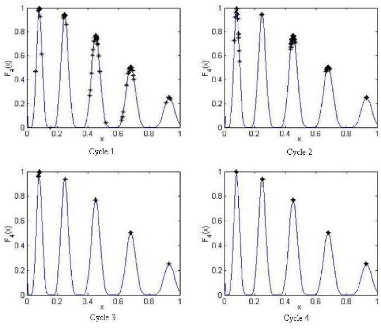
FIG. 3.7 - Placement des individus dans l'espace de recherche
durant l'évolution de MPSO pour la fonction F4
Fonction F5
La figure (3.8) représente la distribution des
particules dans l'espace de recherche durant les différentes
itérations. A la première itération, la valeur d'entropie
est proche de 0.13E - 01, quand l'algorithme converge,
l'entropie prend une valeur plus petite que 2E - 04.
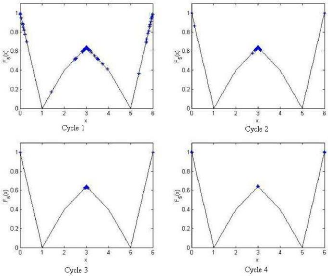
FIG. 3.8 - Placement des individus dans l'espace de recherche
durant l'évolution de MPSO pour la fonction F5
Fonction d'Himmelblau F6
Les résultats obtenus sont récapitulés dans
le tableau (3.4). On peut noter que le centre de chaque classe
détectée est décrit par ses coordonnées (x, y).
L'analyse de ces résultats montre que, dans la
première itération, les quatre classes identifiées ne se
chevauchent pas et que la valeur de l'entropie est relativement grande. Dans la
dernière itération, les optima identifiés sont proche des
optima réel (entropie = 1E - 04). Ceci est confirmé
également en suivant l'évolution de la distribution des
particules dans l'espace de recherche au cours des différents cycles
(figure 3.9).
TAB. 3.4 Evolution de la valeur d'entropie, des centres et des
rayons de classes de la fonction F6.
|
1erCycle(C = 6)
|
2èmeCycle(C = 5)
|
3èmeCycle(C = 5)
|
4èmeCycle(C = 5)
|
|
Centre
|
Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
Centre
|
Rayon
|
|
(2.50,2.49)
|
(2.25,1.62)
|
(3.03, 1.95)
|
(0.59,0.07)
|
(3.02,1.99)
|
(0.16, 0.01)
|
(3.0, 2.00)
|
(0.04, 0)
|
|
(3.52,-1.91)
|
(2.28,0.56)
|
(3.64,-1.84)
|
(0.31,0.01)
|
(3.58,-1.80)
|
(0.08, 0.00)
|
(3.58, -1.80)
|
(0, 0)
|
|
(-3.42,-2.53)
|
(3.33,0.69)
|
(-3.77,-3.11)
|
(0.62,0.07)
|
(-3.78,-3.19)
|
(0.12,0.01)
|
(-3.77,-3.28)
|
(0, 0)
|
|
(-2.39,3.00)
|
(1.98,2.67)
|
(-2.79, 3.17)
|
(0.22,1.05)
|
(-2.81,3.12)
|
(0.02, 0.23)
|
(-2.8, 3.10)
|
(0, 0.02)
|
|
h
|
0.387
|
|
0.05
|
|
6.2E-03
|
|
1E-04
|
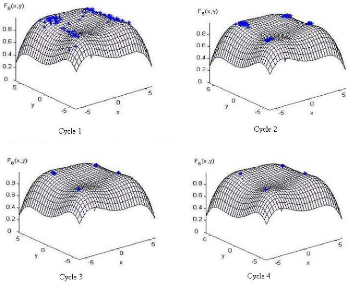
FIG. 3.9 - Placement des individus au cours les différents
cycles du processus d'évolution pour la fonction F6
Fonction de Shekel F7
Le tableau (3.5) représente les résultats obtenus
durant l'évolution du processus.
TAB. 3.5 - Evolution de la valeur d'entropie de la fonction
F7.
|
1er cycle
C = 38
|
2ème cycle
C = 35
|
3ème cycle
C = 29
|
4ème cycle
C = 26
|
5ème cycle
C = 25
|
6ème cycle
C = 25
|
|
h
|
0.436
|
0.177
|
0.01
|
6.2E-03
|
2.3E-03
|
1.12E-05
|
L'analyse de ces résultats montre que 38 classes ont
été détectées à la première
itération, ces classes sont chevauchées et la valeur de
l'entropie est relativement élevée. Au cours de la
deuxième itération, 35 classes sont détectées et
l'entropie continue à décroître. A partir de
cinquième itération, les 25 optima sont localisés.
L'évolution des populations, durant chaque cycle du
processus, est illustrée par la figure (3.10). Au premier cycle, les
particules sont aléatoirement distribuées dans l'espace de
recherche, durant l'évolution du processus, les particules du
sous-essaim sont progressivement groupées autour de plus grand pic de la
fonction F7 (figure 3.11).
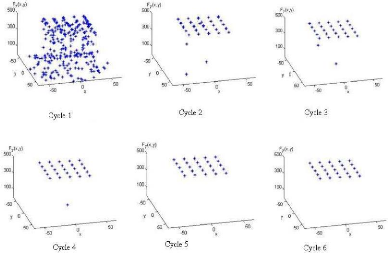
FIG. 3.10 - Placement des individus au cours les
différents cycles du processus d'évolution pour la fonction
F7
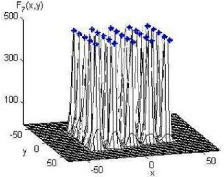
FIG. 3.11 Représentation 3-D de la distribution finale des
individus dans l'espace de recherche de la fonction F7
|
|



