4.3.5 Les méthodes Pareto
L'idée d'utiliser la dominance au sens de Pareto a
été proposée par Goldberg [Goldberg, 1989b] pour
résoudre les problèmes proposés par Schaffer [Schaffer,
1985]. L'auteur suggère d'utiliser le concept d'optimalité de
Pareto pour respecter l'intégralité de chaque critère au
lieu de comparer a priori les valeurs de différentes critères.
L'utilisation d'une sélection basée sur la notion de dominance de
Pareto entraine la convergence de la population vers un ensemble de solutions
efficaces. Ce concept ne permet pas de choisir une alternative plutôt
qu'une autre mais il apporte une aide précieuse au décideur.
Dans les paragraphes suivants, nous définissons tout
d'abord la notion de dominance au sens de Pareto et la frontière de
Pareto, ensuite, nous présentons les techniques évolutionnaires
utilisant cette notion.
4.3.5.1. Optimum de Pareto
Au XIXème siècle, Vilfredo
Pareto, formule le concept suivant [Pareto, 1896] : dans un problème
multiobjectif, il existe un équilibre tel que l'on ne peut pas
améliorer un critère sans détériorer au moins un
des autres critères.
Cet équilibre a été appelé optimum
de Pareto. Un point x est dit Pareto-optimal s'il n'est dominé
par aucun autre point appartenant à l'espace de recherche E.
Ces points sont également appelés solutions non
inférieures ou non dominées.
4.3.5.2. Notion de dominance Un point x E E
domine x' E E si :
Vi, fi(x) fi(x')
avec (4.10)
au moins un i tel que fi(x) <
fi(x')
Dans l'exemple (figure 4.3), les points 1, 3 et 5 ne sont
dominés par aucun autre point. Alors que le point 2 est dominé
par le point 3, et le point 4 est dominé par 3 et 5.
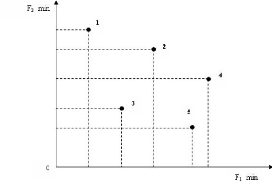
FIG. 4.3 - Exemple de dominance
Un point x E E est dit faiblement non dominé,
s'il n'existe pas de point x' E E tel que :
fi(x') <
fi(x),Vi = 1, ...,k
Un point x E E est dit fortement non dominé, s'il
n'existe pas de point x' E E tel que :
fi(x')
fi(x),Vi = 1, ...,k avec
au moins un i tel que, fi(x')
< fi(x)
4.3.5.3. Frontière de Pareto
La frontière de Pareto est l'ensemble de tous les points
Pareto-optimaux. La figure (4.4) présente la frontière de Pareto
pour un problème à deux objectifs.

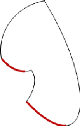
FIG. 4.4 - Exemple de frontière de Pareto
| 


