4.7.2 Résultats numériques
Les paramètres u et u,
utilisés dans l'équation de la mise à jour du vecteur
vitesse (équation 1.1), sont initialisés à 1.5 et
2.5 respectivement pour toutes les fonctions tests, la valeur de
facteur d'inertie r(t) se réduit pendant le processus
[Venter et Sobieski, 2004] selon l'équation (4.19)
r(t + 1) =
r(t)cô (4.19)
cô est une constante entre 0 et 1, la
valeur de cô utilisée est 0.975,
r est intialisé à 1.4 et la taille de l'essaim
est 200.
La figure (4.9) représente les fronts de Pareto des
quatre fonctions tests ZDT1, ZDT2, ZDT3 et ZDT6 trouvés en utilisant
l'algorithme FC-MOPSO. Il est clair que l'algorithme proposé peut
produire presque un front de Pareto uniforme et complet pour chaque
fonction.
4.7.3 Comparaisons avec d'autres techniques
Dans cette section, la comparaison entre les résultats
obtenus par le modèle proposé FC-MOPSO et les techniques :
interactive multi-swarm PSO [Wang et Yang, 2008], MOPSO [Coello et al, 2004] et
MOPSO-CD [Raquel et Naval, 2005].
Le tabeau (4.1) représente la valeur moyenne et
l'écart type des valeurs de GD concernant le modèle FC-MOPSO et
les techniques : interactive multi-swarm PSO, MOPSO et MOPSO-CD.
D'après le tableau (4.1), La valeur de GD indique que
l'algorithme proposé a obtenue la meilleure convergence pour toutes les
fonctions par rapport aux algorithmes multi-swarm, MOPSO et MOPSO-CD. Ceci est
confirmé par le paramètre GD, qui est égal à
3.6E -05 (fonction ZDT1) pour l'algorithme FC-MOPSO et
égal à 8.4E - 05, 2.5E - 02
et 1.0E - 02 pour l'interactive multiswarm PSO, MOPSO et
MOPSO-CD respectivement. La même analyse peut être faite pour les
fonctions ZDT2, ZDT3 et ZDT6.
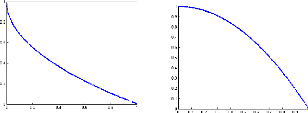
(a) ZDT1 (b) ZDT2
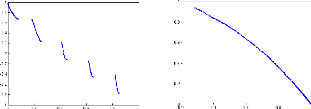
(c) ZDT3 (d) ZDT6
FIG. 4.9 - Le front de Pareto final généré
par l'algorithme FC-MOPSO.
TAB. 4.1 - La moyenne et l'ecart type de la valeur de GD
|
Algorithme
|
ZDT1
|
ZDT2
|
ZDT3
|
ZDT6
|
DTLZ7
|
|
Moyenne
|
|
|
|
|
|
FC-MOPSO
|
3.6E-05
|
9.3E-08
|
4.5E-06
|
5.7E-08
|
8.7E-03
|
|
Interactive multiswarm PSO
|
8.4E-05
|
1.1E-07
|
8.2E-06
|
1.1E-07
|
1.2E-02
|
|
MOPSO
|
2.5E-02
|
4.0E-03
|
7.3E-03
|
6.9E-03
|
1.8E-02
|
|
MOPSO-CD
|
1.0E-02
|
1.1E-02
|
1.3E-02
|
2.8E-02
|
1.9E-02
|
|
Ecart type
|
|
|
|
|
|
FC-MOPSO
|
1.88E-04
|
3.5E-07
|
8.4E-06
|
2.9E-07
|
1.2E-04
|
|
Interactive multiswarm PSO
|
2.6E-04
|
4.6E-07
|
2.2E-05
|
4.2E-07
|
3.2E-04
|
|
MOPSO
|
2.3E-03
|
6.0E-07
|
4.8E-04
|
1.0E-02
|
8.4E-02
|
|
MOPSO-CD
|
3.4E-03
|
4.9E-05
|
1.5E-04
|
1.5E-03
|
8.5E-04
|
Puisque le front de Pareto de DTLZ7 est l'intersection de la
droite avec l'hyperplan, la convergence est difficile. Cependant, FC-PSOMO
arrive à améliorer la valeur de GD par rapport aux autres
algorithmes.
Le tableau (4.2) représente la moyenne et
l'écart type des valeurs de SP pour les quatre MOPSO algorithmes
appliqués aux cinq fonctions tests. La valeur de SP montre que les
solutions générées par l'algorithme proposé sont
mieux distribuée que celles obtenues par les autres trois algorithmes
pour toutes les fonctions tests.
TAB. 4.2 - La moyenne et l'écart type de la valeur de
SP
|
Algorithme
|
ZDT1
|
ZDT2
|
ZDT3
|
ZDT6
|
DTLZ7
|
|
Moyenne
|
|
|
|
|
|
FC-MOPSO
|
3.4E-04
|
8.7E-05
|
6.3E-04
|
1.19E-04
|
1.1E-02
|
|
Interactive multiswarm PSO
|
3.2E-03
|
3.8E-04
|
4.2E-03
|
8.8E-04
|
1.3E-02
|
|
MOPSO
|
1.1E-02
|
1.0E-02
|
2.3E-02
|
2.4E-03
|
8.4E-02
|
|
MOPSO-CD
|
1.6E-02
|
1.0E-02
|
1.6E-02
|
2.8E-03
|
4.8E-02
|
|
Ecart type
|
|
|
|
|
|
FC-MOPSO
|
6.5E-03
|
2.56E-04
|
2.3E-03
|
7.3E-04
|
1.4E-04
|
|
Interactive multiswarm PSO
|
7.3E-03
|
3.4E-04
|
1.4E-03
|
5.7E-04
|
1.9E-02
|
|
MOPSO
|
6.8E-03
|
8.4E-03
|
4.8E-04
|
9.5E-04
|
2.8E-02
|
|
MOPSO-CD
|
3.3E-03
|
3.4E-03
|
4.3E-03
|
5.7E-04
|
6.3E-02
|
Puisque le front de Pareto de ZDT3 n'est pas
uniformément distribué, cette fonction peut être
utilisée pour étudier la capacité de l'algorithme à
maintenir une bonne distribution de solution. D'après les
résultats obtenus pour la fonction ZDT3, on peut conclure que la
distribution des solutions est améliorée par l'utilisation de
FCMOPSO. En fait, la vaeur de SP est égal à 6.3E
-04 pour le modèle FC-MOPSO et égal à
4.2E-03, 2.3E-02 et
1.6E-02 pour interactive multi-swarm PSO, MOPSO et MOPSO-CD
respectivement. La même analyse peut être faite pour les fonctions
ZDT1, ZDT2, ZDT6 et DTLZ7.
Les résultats de simulation montre que l'algorithme
proposé accompli les meilleurs performances par rapport aux autres
méthodes en terme de la qualité des solutions trouvées,
prouvée par les valeurs de GD et de SP.
| 


