Chapitre 2
* + ?, - * +
* + représente le vecteur des forces surfaciques.
2.9. Assemblage et conditions aux limites 2.9.1.
Définition de l'assemblage
L'assemblage est l'opération qui consiste à
construire la matrice globale , - et le vecteur global des sollicitations * +
à partir des matrices élémentaires , - et des vecteurs
élémentaires des sollicitations * +.
2.9.2. Les règles et étapes de
l'assemblage
Les règles d'assemblage sont définies par la
relation :
?
les matrices élémentaires étant initialement
exprimées dans le repère local propre à chaque
élément, on les exprime dans le repère global avant de
procéder à leur sommation étendue au domaine
maillé.
La procédure qui consiste à exprimer une matrice
élémentaire en repère global s'appelle l'expansion
de matrice
Ainsi donc nous avons :
, - ?, -
* + ? * +
avec * +=* + * +
, -, * +, * + sont les matrices et vecteurs
élémentaires expansés.
60 /176
L'assemblage se déroule donc principalement en deux
étapes :
61 /176
Chapitre 2
? construction des matrices étendues par expansion des
matrices et vecteurs élémentaires [
ke], tf }, tf }
;
? addition des matrices et des vecteurs
étendus.
62 /176
Chapitre 3
Chapitre 3 : Etude de quelques
exemples d'éléments finis
Sommaire
3.1. Elément fini linéaire à deux
noeuds 63
3.2. Elément fini triangulaire plan à trois
noeuds 64
3.3. Elément fini tétraédrique
à quatre noeuds 66
Chapitre 3
3.1. Elément fini linéaire à deux
noeuds 3.1.1. Définition
Il s'agit d'un élément de type poutre pour le
calcul des réseaux de poutre chargés.
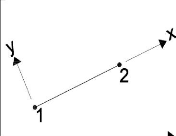
Figure 3.1 : Elément de Poutre plan.
Soit E, A, I, L ses caractéristiques mécaniques et
géométriques. 3.1.2. Matrice de rigidité
élémentaire
3.1.2.1. Poutre en flexion simple
Pour une poutre qui travaille en flexion simple,
l'élément fini utilisé possède deux degrés
de liberté par noeuds (1 degré de liberté en
déplacement, 1 degré de liberté en rotation), soit au
total quatre degrés de liberté.

63 /176
Figure 3.2 : Elément fini de poutre avec deux
degrés de liberté par noeuds.
Chapitre 3
La matrice de rigidité élémentaire
utilisée dans les calculs est :
|
12
|
6L
|
--12
|
6L
|
|
El 6L
|
4L2
|
--6L
|
2L2
|
|
[K ] = L3 --12
|
--6L
|
12
|
--6L
|
|
6L
|
2L2
|
--6L
|
4L2
|
3.1.2.2. Poutre en flexion composée
Cet élément possède trois degrés
de liberté par noeuds (2 degrés de
liberté en déplacement et 1 degré de liberté en
rotation), soit au total six degrés de liberté.
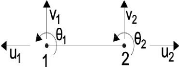
Figure 3.3 : Elément fini de poutre avec trois
degrés de liberté par noeuds.
La matrice de rigidité élémentaire
utilisée dans les calculs est :
64 /176
--
L2 L L2 L
3.2. Elément fini triangulaire plan à trois
noeuds 3.2.1. Définition
Il s'agit d'un élément à trois
noeuds, utilisés pour les problèmes de contrainte plane, de
déformations planes ou d'axisymétrie.
65 /176
| 


