Modélisation et simulation par éléments finis : cas d'un tablier de pont.

Chapitre 1

- Les trois composantes du champ de déplacement A = (u, v, w) :

( )

( )

( )

- les six composantes du tenseur de petites déformations :

( )

( )

( )

- les six composantes du tenseur des contraintes :

Pour résoudre un tel problème, nous devons disposer de 15 équations. Ces équations sont :

Les trois équations d'équilibre [2] :

Sur V :

9 /176

10 /176

Chapitre 1

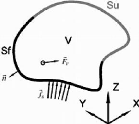
Figure 1.3: Solide de domaine V soumis à des chargements

Les six relations géométriques de Cauchy [2] :

Ces équations assurent que les déformations dérivent d'un champ de déplacement

( )

( )

( )

La loi de Hooke sous forme directe pour un matériau isotrope, élastique et linéaire [2] :

[	(	)]
[	(	)]
[	(	)]

( )

( )

( )

Ces équations sont assorties de conditions aux limites en pression ou en déplacement :

11 /176

Chapitre 1

Sur Sf : {

Sur S_u :

1.5.2. Les différentes méthodes de résolution

La résolution des équations de la théorie de l'élasticité peut être menée de plusieurs manières en fonction des quantités prises comme inconnues et on distingue généralement trois grandes méthodes de résolution :

- La résolution du problème en fonction des déplacements : dans ce cas, on considère que les fonctions inconnues sont les composantes : u, v, w du vecteur déplacement ;

- La résolution en fonction des contraintes : dans ce cas, on considère que les fonctions inconnues sont les composantes des contraintes normales et tangentielles ;

- La résolution du problème sous forme mixte : dans ce cas, on considère comme fonctions inconnues, une partie des fonctions déplacements et l'autre partie des fonctions contraintes.

En théorie de l'élasticité, l'on est souvent conduit à résoudre les équations de Lamé qui constituent un modèle décrivant le comportement, en déformation, d'un solide sous des conditions de chargement et de fixation connues (conditions aux limites).

La résolution du problème de la théorie de l'élasticité consiste à déterminer en tout point des coordonnées cartésiennes un vecteur de composantes u, v, w caractérisant un petit déplacement de ce point au cours de la déformation du milieu.

Nous proposerons dans la suite la méthode de GALERKIN pour la résolution des équations de Lamé, afin de simuler le comportement d'un solide à surface lisse, sous des conditions aux limites en déplacement et soumis à un chargement volumique.

12 /176

Chapitre 1

1.6. Méthode de GALERKIN pour la résolution des équations de Lamé

1.6.1. Modèle mathématique étudié

Supposons qu'un solide élastique occupe dans l'espace à trois dimensions un domaine 0 délimité par une surface fermée S.

Nous obtenons les équations de Lamé, caractérisant le comportement, sous la forme suivante [2] :

(A+u) V ( divA) (1.1)

Avec la condition aux limites en déplacement (condition de type Dirichlet) :

(1.2)

Où A et u sont les coefficients de lamé tels que :

(1 + v)(1 -- 2v)

(1 + v) , 2 (À. + u)

(y étant le coefficient de poisson et E le module de Young)

A = A(x, y, z) = ( u(x, y, z) , v(x, y, z) , w(x, y, z)) E R³ sont les

composantes du vecteur déplacement en chaque point du solide de 0 délimité par la surface S.

Ao = (uo, _vo,wo) est le vecteur déplacement imposé à la surface du solide ; p est la densité du solide.

P = ( P₁, P₂, P₃) la charge constante.

1.6.2. Transformation du modèle mathématique L'équation vectorielle (1.1) peut alors s'écrire sous la forme :

Chapitre 1

( ) ( )

( ) ( ) (1.3)

( ) ( )

Nous allons chercher la solution de ces équations sous la forme

,

Où est un vecteur harmonique c'est-à-dire : ,

???????????

est le gradient d'une fonction scalaire c'est-à-dire : Nous adoptons les hypothèses suivantes :

13 /176

{ (1.4)

Soit ( ) ; alors {

(1.5)

(1.6)

Puisque ( ), on a :

{

En substituant (1.6) dans (1.3) on a :

(		, (		(		(
	)		)		)		)-
(
	)	, (	)	(	)	(	)-
(		, __ (		(		(
	)		__)		)		)-

(1.7)

En prenant en compte (1.5), le système d'équations (1.7) devient :

Chapitre 1

( ) , ( ) ( ) ( )-

( ) , ( ) ( ) ( )-

( ) , ( ) ( ) ( )-

(1.8)

En réorganisant le système d'équations ci-dessus, on aboutit au système suivant :

, ( )-

0 ( )1 (1.9)

{ , ( )-

(1.9)		,(	)	(	)
		,(	)	(	)
	{	,(	)	(	)

-

- (1.10)
-

14 /176

L'intégration de ce système d'équations nous donne :

( ) ( ) ( ) ( ) ( ) .. ( )

(1.11)

Où f1, f2, f3 sont des fonctions arbitraires.

Sans perdre la généralité et pour la compatibilité du système, nous supposons que :

( ) ( )

( ) ( ) (1.12)

( ) .. ( )

15 /176

Chapitre 1

En substituant (1.12) dans (1.11), on ramène le système (1.11) sous forme de l'équation de Poisson:

( ) ( ) (1.13)

En remplaçant dans cette équation le coefficient de Poisson par son expression, on obtient :

( ) , ( ) (1.14)

			Ou , ( )- ( )	(1.15)

1.6.3. Résolution de l'équation de Poisson par l'approche variationnelle de GALERKIN

1.6.3.1. Méthode de GALERKIN

La méthode de GALERKIN consiste en ce qui suit :

Nous cherchons une solution de l'équation de Poisson (1.15) sous la forme d'une combinaison linéaire de fonctions linéairement

indépendantes vérifiant la condition aux limites (1.4), c'est-à-dire Ø/S=0.

On substitue la solution approchée dans (1.15) et on multiplie par les fonctions linéairement indépendantes ; ensuite on intègre par partie suivant le domaine 0 pour obtenir une relation intégrale à partir de laquelle on détermine les coefficients de la combinaison linéaire.

1.6.3.2. Application de la méthode de GALERKIN En multipliant l'équation (1.14) par une fonction non nulle on a : ( ( ) , ( )-) En intégrant suivant 0, on obtient :

(1.16)

? ( ( ) , ( )-) (1.17)

16 /176

Chapitre 1

? ( )

( ) ? , ( )-

(1.18)

Par une intégration par parties, on a :

? ( ) ? , (

( )

)- pour ö/S = 0. En posant , on a : ? (. / ( ) ? , ( . / . / ) )-

(1.19) (1.20)

Pour l'application, nous considérons le domaine d'intégration 0 défini par :

* ( )

+

Figure 1.4 : Représentation 3D du domaine 0

17 /176

Chapitre 1

Considérons la partie S1 de la surface S définit par :

* ( ) +

La condition se présente alors comme un cas particulier de

la condition aux limites (1.4)

Les conditions aux limites (1.4) et (1.5) sont équivalentes aux conditions suivantes :

{ (1.21)

{ (1.22)

{ (1.23)

Choisissons un point arbitraire ( )

( ) ( ) les fonctions prennent les valeurs

suivantes :

( ) les fonctions prennent les valeurs suivantes :

( )

( ( ) ) ( ) ( ) ( )

( )( )

( )

18 /176