|

Ecole Supérieure du Professorat et de
l'Education - Université Paris Est Créteil
Le sens de la numération décimale
à travers le groupement par 10
Option de recherche 1.1
Apprentissage mathématiques à
l'école : approche didactique

Sous la direction de : Mme HOROKS
Etudiante : SETTBON Victoria Ð numéro
étudiant : 21001855
Année Universitaire : 2014 - 2015
~ 2 ~
Sommaire
Sommaire 2
Introduction 4
Le cadre théorique 7
I. Quelques éléments théoriques et
historiques 7
II. Les premiers apprentissages de la numération 9
A. La place du nombre dans la scolarité obligatoire 9
B. Les finalités et principes de la numération
10
C. Les stratégies de dénombrement : du
dénombrement terme à terme aux
groupements 12
Etayage du questionnement 13
I. Le groupement par écrit, le groupement par oral 13
II. Le groupement par 10 et autres groupements 20
III. La manipulation et le matériel 22
IV. Le groupement en lien avec les opérations 24
Synthèse 28
Problématique et hypothèse 31
I. Présentation de la problématique 31
II. Hypothèse 31
L'expérimentation 32
I. Le choix de l'expérimentation 32
II. Le déroulement de la séquence 33
III. Présentation des cinq séances 34
Séance 1 34
~ 3 ~
Séance 2 35
Séance 3 36
Séance 4 38
Séance 5 38
Analyse 39
I. Analyse a priori 39
Séance 1 39
Séance 2 41
Séance 3 42
Séance 4 44
Séance 5 45
II. Analyse a posteriori 46
Séance 1 46
Séance 2 48
Séance 3 49
Séance 4 51
Séance 5 54
III. Interprétation 56
Conclusion 60
Bibliographie 62
Annexes 64
~ 4 ~
Introduction
Etudiante en première année de Master MEEF
(Métiers de l'enseignement, de l'éducation et de la formation) et
afin de suivre la formation qui me permettra de devenir professeur des
écoles, je me dois d'élaborer une note de recherche dans le
thème d'une option choisie. Mon option est la « didactique des
mathématiques ». Ce choix s'est fait par rapport à
l'importance des mathématiques à l'école primaire, mais
également aux difficultés que peut engendrer cette
matière.
Durant ces deux années de Master, nous sommes
invités à nous interroger sur un sujet choisi, relié
à un domaine d'apprentissage, qui nous permettra de trouver des
réponses concrètes pour faire avancer notre recherche. Cet
écrit nous permettra d'approfondir notre formation dans le professorat
des écoles et de pouvoir transmettre plus aisément aux
élèves, une notion perçue comme étant assez
ambig·e au départ. Le thème est donc à choisir avec
précaution puisqu'il doit être aussi intéressant qu'utile
et nous permettre d'entrer en situation de recherche.
Mes interrogations concernent le thème complexe de la
numération à l'école primaire et plus
particulièrement celui du système décimal. En effet, ayant
effectué des stages d'observation et de pratique accompagnée,
j'ai pu remarquer que l'enseignement des mathématiques à
l'école est un enseignement de base qui doit être transmis de
façon claire, afin d'éviter au maximum les confusions des
élèves. J'ai donc voulu en repérer les difficultés
dans le but que les différentes notions enseignées me paraissent
un peu plus évidentes. Le domaine de la numération, et surtout
celui de la compréhension du système conventionnel
français, m'a parut être un apprentissage de base qu'il serait
intéressant d'approfondir.
~ 5 ~
Les apprentissages fondamentaux et les bases de la
numération se font principalement au cours préparatoire. Tout au
long de la journée, les enfants comptent, apprennent à
écrire les nombres, à les oraliser et à s'en servir pour
quantifier. Quant aux enseignants, ils cherchent constamment à faire des
liens entre la numération et tout autre domaine lié au
fonctionnement de la classe pour que les élèves atteignent un
automatisme quotidien concernant l'apprentissage de la numération
(Exemple : « combien y a-t-il d'élèves
absents/présents aujourd'hui ? », « combien
d'élèves mangent à la cantine ? » etc.).
J'ai donc voulu savoir comment les professeurs des
écoles s'y prennent pour que les élèves acquièrent
une bonne compréhension de la numération et comment ces derniers
assimilent le concept de « groupement par dix » pour le
réutiliser tout au long de leur scolarité.
Les questionnements au départ restent naïfs et
très généraux mais je me suis posée des questions
telles que :
Pourquoi un système conventionné en base 10
?
En quoi le travail de groupement par 10 peut-il
permettre aux élèves de comprendre le sens de la
numération décimale, et en particulier les conventions
qui
la définissent ?
Est-ce qu'il existe une méthode favorable
à une meilleure compréhension de
la numération pour les élèves en
difficultés ?
Quelles approches pédagogiques permettraient de
donner du sens à cet
apprentissage ?
Mes questions tournaient beaucoup autour de
l'élève et ma principale difficulté était de savoir
comment j'allais pouvoir observer que les élèves étaient
passé d'un dénombrement terme à terme (c'est-a-dire d'un
comptage unité par unité, nombre par nombre) à un
dénombrement par groupements, qui amènera par la suite aux
groupements « unités, dizaines, centaines etc. » du
système décimal français et qui leur
permettra une meilleure compréhension de ce dernier. Il
m'a donc fallut trouver un autre questionnement plus précis et
observable grâce à une expérimentation.
Afin d'approfondir ces questionnements beaucoup trop
généraux, je me suis tournée vers des articles qui m'ont
permis de rétrécir le champ de ma question de recherche mais
également d'éclaircir ce thème complexe qu'est la notion
de groupement décimal en numération.
Dans le but de vous présenter une problématique
plus fine concernant ce sujet, j'apporterai dans un premier temps des notions
théoriques sur la numération et le domaine du groupement
décimal. Puis, dans un second temps, j'expliciterai les
différentes méthodes de groupement utilisées lors
d'expérimentations (tirées d'articles), dans le but de trouver
moi-même une expérimentation pouvant répondre à la
problématique choisie.
~ 7 ~
Le cadre théorique
I. Quelques éléments théoriques et
historiques
La numération a pour but d'exprimer une quantité
grâce à des signes choisis. Les signes sont les chiffres, dans
notre système français actuel. Il a existé
différents signes à travers les différentes époques
(exemple : chiffres romains, numération égyptienne...). En
France, il existe dix signes (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) qui nous permettent
de réaliser une quantité indéfinissable de nombres
grâce à la combinaison de ces mêmes signes. Si nous pouvons
combiner ces signes, c'est grâce à la base choisie de notre
système français de numération qui est la base 10. La base
est un choix de groupement ; selon les pays cette base peut varier. En effet,
le choix de celle-ci entraine la création de règles selon
lesquelles les différents signes pourront être combinés
afin de former des nombres.
Exemple : en France,
- lorsque l'on a dix unités, on peut les «
échanger contre une dizaine »
- lorsque l'on a dix dizaines, on peut les « échanger
contre une centaine » - et ainsi de suite avec les milliers, les millions,
les milliards etc.
S'il existe ce genre de règles dans le domaine de la
numération, c'est pour que les Hommes n'aient pas à créer
autant de signes que de nombres pouvant exister. En effet, il existe une
infinité de nombres qui ne peuvent évidemment pas être
associés à une infinité de signes puisque le cerveau
humain ne serait pas capable de retenir un signe par nombre. La création
de base dans la numération est donc un moyen économique pour
combiner un nombre fini de signes (en France, dix signes) afin de créer
une quantité infinie de nombres.
D'autres règles existent telles que le sens de
l'écriture des nombres ou encore la manière d'oraliser ces
nombres. Ces règles constituent le système de
numération.
Les chiffres, en France, sont souvent appelés «
chiffres arabes », mais étaient déjà connus des
Indiens qui utilisaient un système décimal proche du notre.
Dans un système de numération, si la base est un
nombre entier, le nombre de chiffres utilisés dans la
représentation des nombres est strictement égal à la
valeur de la base. Ces bases diffèrent à travers les
époques et les civilisations.
Le système positionnel de numération existe
depuis le IIIème millénaire avant Jésus Christ. Les
mathématiciens babyloniens de l'époque utilisaient un
système séxagésimal (base 60) et la transmission de ce
système en Occident s'est faite au VIIème siècle
grâce à un moine syrien, ayant attesté qu'il existait neuf
signes indiens (sans le zéro). Au IXème siècle,
l'algébriste arabe Al-Khwarismi rédige le traité « De
numero Indorum » (en latin, « Des chiffres indiens »), et c'est
à partir de là que la transmission est véritablement faite
en Occident.
Les systèmes positionnels de numération sont
conformes à des bases qui peuvent varier. La base définit la
puissance qui déterminera l'ordre de grandeur (donc la place du chiffre)
dans un nombre ; en effet, plus la puissance est faible, plus le chiffre se
trouve à droite. Dans notre système d'écriture
français, nous écrivons de gauche à droite et dans le
système de numération, le chiffre ayant la plus grande valeur
(donc la plus forte puissance) est placé en premier (donc le plus
à gauche). Prenons l'exemple de notre système décimal de
numération pour mieux illustrer ce propos :
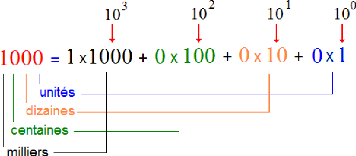
Le zéro signifie l'absence de groupement (exemple : 108
signifie qu'il y a une centaine, zéro dizaine et huit unités).
~ 9 ~
De nombreux systèmes positionnels ont été
utilisés par les peuples et à travers les époques :
- Le système binaire - base 2 (utilisé en
informatique)
- Le système quinaire - base 5 (utilisé jusqu'au
XXème siècle notamment par les
peuples africains)
- Le système sénaire - base 6
- Le système octal - base 8
- Le système décimal - base 10 (système
étant aujourd'hui le plus utilisé et le plus
répandu puisqu'utilisé par rapport au nombre de
doigts des deux mains)
Puis les systèmes au-delà du système
décimal ; duodécimal (base 12), hexadécimal (base 16),
vigésimal (base 20) ou encore sexagésimal (base 60 permettant de
mesurer le temps des secondes jusqu'aux heures / 60sec = 1 min, 60 min = 1h
mais 60h ? 1 jour et 60 centièmes ? 1 sec).
II. Les premiers apprentissages de la
numération
A. La place du nombre dans la scolarité obligatoire
Le nombre a deux fonctions principales à l'école :
- Il est utilisé comme « outil » lorsque les
élèves en ont besoin pour résoudre des problèmes,
pour mémoriser une quantité, pour compter ou pour calculer par
exemple.
- Après avoir été utilisé comme
outil, le nombre sera étudié comme « objet » par les
élèves, objet qu'ils pourront comprendre et étudier de
façon à part entière (Cf article de Douady R., Dialectique
outil-objet, 1984)
A l'école, on utilise le nombre pour mémoriser,
compter, dénombrer, calculer, résoudre des problèmes, mais
on l'utilise également dans les situations de partage, de calculs ou de
comparaison. Le nombre est constamment sollicité à l'école
et l'apprentissage des nombres est un apprentissage premier dans le milieu
scolaire.
Selon le Bulletin Officiel hors série n°3 du 19
juin 2008, un élève de CP doit « Connaitre (savoir
écrire et nommer) les nombres entiers naturels inférieurs
à 100 »
~ 10 ~
(p. 33), un élève de CE1 doit connaître
ceux inférieurs à 1000 et « Ecrire des suites de nombres de
10 en 10, de 100 en 100, etc. », tout en sachant ranger, encadrer et
comparer ces nombres. Au cycle 3 (CE2, CM1, CM2) l'évolution des
apprentissages va continuer et les élèves devront connaitre des
nombres de l'ordre du million et du milliard et savoir s'en servir. Bien que
les élèves commencent généralement à
calculer dès le cycle 1, il est important pour eux de comprendre le
fonctionnement de la numération décimale dès le cycle
2.
Dans ce bulletin officiel, il est également
précisé qu'au cycle 2 « Les problèmes de
groupements et de partage permettent une première approche de la
division pour de nombres inférieurs à 100. » (p. 18)
pour le cycle 3.
A partir du cycle 3, il est dit que les élèves
doivent connaître les « principes de la numération
décimale de position : valeur des chiffres en fonction de leur position
dans l'écriture des nombres. » (p. 22), puis c'est lors de ce
cycle et dans leur futur scolarité qu'ils vont commencer à
travailler sur les nombres décimaux.
D'après les programmes du collège (B.O n°6
du 28 août 2008) : « Les nombres sont au début et au
coeur de l'activité mathématique. L'acquisition des principes de
base de la numération, l'apprentissage des opérations et de leur
sens, leur mobilisation pour des mesures et pour la résolution de
problèmes sont présents tout au long des apprentissages.
»
De façon évidente, la numération est
présente dans toute la scolarité d'un élève de la
maternelle à la fin de la scolarité obligatoire. Il est donc
important que l'élève puisse donner du sens à ce domaine
et comprendre comment fonctionne le système décimal afin
d'éviter des lacunes tout au long de sa scolarité. C'est pour
cela qu'il est intéressant d'enseigner les principes de la
numération décimale le plus tôt possible, en
privilégiant le cycle des apprentissages fondamentaux.
B. Les finalités et principes de la
numération
La numération peut être utilisée dans un
but ordinal qui, comme son nom l'indique, va servir à donner un ordre
à chaque élément d'un ensemble (ex : le premier,
~ 11 ~
le troisième, mais aussi les numéros de rue
etc.). Elle peut être également utilisée dans un but
cardinal, afin d'exprimer une quantité, de représenter des
grandeurs ou des proportions. Les aspects ordinal et cardinal sont tous deux
travaillés à l'école, de façon plus ou moins
simultanée.
La numération peut être écrite ou orale et
l'un des objectifs de l'école est que l'élève sache
identifier les écritures chiffrées des nombres, identifier les
nombres à l'oral mais également associer les écritures
chiffrées aux prononciations orales auxquelles elles correspondent et
inversement.
Afin d'appréhender la numération, les
enseignants utilisent beaucoup les situations de dénombrement.
Le dénombrement consiste à compter les
éléments d'une collection et à en donner la
quantité. Selon Gelman (1983), il existe cinq principes du
dénombrement dans la numération :
- La correspondance terme à terme ; c'est-à-dire
qu'à chaque unité on fait correspondre un terme (exemple : la
troisième unité comptée aura pour terme associé
3).
- La suite stable ; les mots doivent toujours être
cités dans le même ordre.
- Le principe cardinal ; le dernier mot nombre prononcé
fait référence à la quantité d'objets
dénombrés.
- L'indifférence de l'ordre ; les objets d'une
collection peuvent être comptés dans n'importe quel ordre (en
faisant attention de ne pas en oublier ou de ne pas compter plusieurs fois le
même élément.
- Le principe d'abstraction ; on dénombre sans faire
attention aux caractéristiques des objets.
Lorsque les élèves dénombrent, ils
doivent mettre en place ces cinq principes de façon simultanée.
S'ils n'y arrivent pas, ils commettent des erreurs et c'est en cela que l'on
peut remarquer que les cinq principes n'ont pas été
assimilés de façon correcte. Le dénombrement, tout comme
la comptine numérique, est l'une des bases de la numération. Si
les bases ne sont pas correctement mises en place au cours de la
scolarité d'un enfant, il présentera des lacunes dans les
situations à venir.
C. Les stratégies de dénombrement: du
dénombrement terme à terme aux groupements
Le dénombrement est, comme dit ci-dessus, un type de
problème très important de la numération. Grâce au
dénombrement, l'élève pourra quantifier une collection,
représenter cette collection grâce à une écriture
chiffrée et pourra également chercher des stratégies lui
permettant de dénombrer plus rapidement. Parmi ces stratégies
figure le groupement.
Le groupement est le fait que les élèves vont
associer des éléments d'une collection par paquets (au moins
deux), afin de dénombrer de façon plus stratégique. Il est
vrai que lorsque les élèves dénombrent les objets un par
un, cela prend tout d'abord plus de temps et il y a un risque de devoir tout
recommencer, si il y a un arrêt au cours du dénombrement, ou si
l'élève n'a pas une mémoire de travail effective
(mémoire qui s'occupe du traitement des informations à court
terme), lui permettant de retenir le dernier nombre dénombré.
Les enseignants, aujourd'hui, amènent les
élèves aux groupements afin qu'ils aient une connaissance en
profondeur du système de numération français, qui a pour
principe le groupement par dix (système décimal). Ils cherchent
à donner du sens aux apprentissages des élèves. Rappelons
que la stratégie de groupement ne fait pas partie des programmes
officiels en tant qu'apprentissage à part entière, mais qu'il est
une aide pour les calculs futurs (additions, divisions, multiplications etc.).
Les enseignants l'utilisent également dans le but que leurs
élèves abandonnent le dénombrement terme à terme
(c'est-à-dire unité par unité) et privilégient le
groupement pour une compréhension plus poussée de la
numération. Il s'agit aussi d'une des dernières occasions de
manipuler réellement une quantité, avant l'entrée dans un
travail sur l'écriture chiffrée pour représenter des
quantités importantes.

~ 13 ~
Etayage du questionnement
Afin d'affiner mon questionnement et dans le but qu'il
devienne une problématique testable grâce à une
expérimentation, j'ai pris comme supports théoriques certains
articles abordant le thème de la numération à
l'école élémentaire, et plus particulièrement le
domaine du groupement.
Je garde comme question naïve « Existe-t-il une
méthode favorable à une bonne compréhension de la
numération ? » (p.4) et la transforme en « Est-ce que
l'approche par les groupements favorise les apprentissages de la
numération ? Comment donner du sens à cet apprentissage et en
particulier aux conventions liées à l'écriture des nombres
? »
Je centre ma recherche sur cette question naïve car il me
semble intéressant d'étudier les différentes
méthodes ou techniques utilisées en termes de groupements qui
aideront les élèves à mieux appréhender le
système de numération décimale.
Ci-dessous, j'expliciterai les différentes
méthodes et techniques de groupements utilisées dans les
différents textes que j'ai pu lire.
I. Le groupement par écrit, le groupement par
oral
Dans les différents articles que j'ai pu lire, la
technique de groupement seulement évoquée est celle du groupement
par écrit. En effet, certaines études ont été
menées pour voir comment réussir à amener les
élèves aux groupements, dans le but qu'ils acquièrent une
bonne compréhension de la numération.
C'est grâce à ces différents articles que
j'ai pu remarquer l'importance de l'écriture dans la
compréhension de la numération.
Selon Bednarz et Janvier (1984) et leur article lié aux
difficultés que suscite la numération dans son apprentissage, on
peut relever au cycle 1 une grande insistance
mise sur le passage de l'écriture symbolique du nombre
« chiffre, position » à la symbolisation « unités,
dizaines, centaines,... ». Pour les élèves, un nombre est
une suite de chiffres ; ils ne donnent aucun sens aux mots dizaines, centaines
etc. et ne s'intéressent qu'à
la place de l'écriture (non à son sens). Aussi, ces deux auteurs
soulignent le fait que toute représentation d'un nombre apparait selon
un alignement reprenant l'ordre de l'écriture conventionnelle du nombre
: l'enfant fait une association directe entre un nombre et une position.
Exemple :

Ici, on remarque bien que l'alignement et la position des
dessins dans le premier cas va inciter l'élève à
écrire le nombre 231, sans pour autant comprendre qu'un carré est
une centaine, un rectangle est une dizaine et un bâtonnet est une
unité. Tandis que dans le deuxième cas de figure, si les
élèves ne donnent pas de sens aux dessins
représentés, ils auront beaucoup de difficultés à
trouver le nombre correspondant, puisqu'ils sont placés dans le plan de
façon inhabituelle. Les auteurs montrent ainsi l'aide que les
différents manuels ou même les enseignants offrent aux
élèves dans l'écriture des nombres, sans prêter
attention au sens.
Elles relèvent aussi que les élèves ont
une conception de la complexité du nombre uniquement basée sur la
taille : plus un nombre est grand, plus il est compliqué,
difficulté qui posera surtout problème lors de l'introduction des
nombres décimaux.
Dans ce texte, les auteurs relèvent de nombreuses
difficultés liées à l'apprentissage de la
numération que nous verrons par la suite. Ce qu'elles recommandent aux
enseignants est de moins s'axer sur l'écriture ou sur les règles
qu'ils

transmettent aux élèves de façon assez
mécanique et de mettre d'avantage l'accent sur le sens que l'enfant doit
accorder à l'écriture. En effet, les enseignants pensent peut
être que la signification véritable de la position d'un chiffre
dans un nombre est une notion qui coule de source aux yeux des
élèves, c'est pour cela que lorsque l'enfant rencontre une
difficulté, il n'a aucun recours autre que celui de l'écriture
pour l'aider puisqu'il n'aura pas donner de sens à la numération
elle-même.
On peut noter des limites à cet article puisqu'il date
d'une trentaine d'années et il existe de nouvelles études
beaucoup plus actuelles, auxquelles s'intéresser. Aussi, l'étude
a été faite au Canada ; bien que les programmes en
numération soient très proches des programmes français,
les pays comportent des différences, dont le fait qu'il n'y ait pas
d'école maternelle au Canada et qu'en France, l'apprentissage de la
numération se fasse dès cette dernière. Cela pose donc la
question des effets de ces choix, qu'on pourrait éventuellement analyser
en comparant les deux pays.
Un article plus récent d'Aigoin et Guebourg (2004) va
nous permettre de réaliser à quel point l'écriture est
importante dans la notion de groupement, surtout lorsqu'il s'agit d'un moyen de
communication entre deux groupes. Dans cet article, les auteurs font un rapport
de l'écart qui peut exister entre les élèves ayant une
bonne compréhension du système de numération et ceux ayant
des lacunes concernant celui-ci.
En effet, à partir d'une expérimentation faite
en classe de CP, les élèves sont placés face à une
situation problème (situation dans laquelle l'élève est
confronté à trouver des solutions à un problème de
façon autonome, dans le but d'acquérir de nouvelles
connaissances), dans laquelle ils doivent dénombrer un nombre x de
gommettes et le transmettre à un autre élève de
façon écrite (expérience du « bon de commande
»).
Les deux groupes A et B étant confrontés sont
respectivement les groupes qui ont :
- Une bonne compréhension de la numération
(comptine numérique jusqu'à 100 (voire au-delà),
association de l'écriture chiffrée au mot-nombre, comparaison des
nombres, classement dans l'ordre croissant ou décroissant,
élaboration d'une file numérique etc.)

- Une compréhension moins évidente de la
numération (les élèves ont connaissance de la chaine
numérique jusqu'à 30 et au-delà)
Nous avons besoin de connaître l'expérimentation
mise en place par les auteurs afin de comprendre l'importance du groupement
écrit.
Cinq équipes sont mises en places. Chaque équipe
comprend un élève du groupe A et plusieurs élèves
du groupe B.
La première expérience consiste à ce que
les élèves du groupe A dénombrent la quantité
d'objets qui leur est donnée (sur une feuille A3), puis la transmettent
par l'intermédiaire d'un bon de commande aux élèves du
groupe B. Les élèves du groupe B doivent déchiffrer le bon
de commande et donner l'exact nombre de gommettes aux élèves du
groupe A afin qu'ils puissent les coller sur chaque objet de la collection.
Les élèves n'ont pas le droit de communiquer
entre les groupes autrement que par le bon de commande, ce qui crée une
situation d'incompréhension entre les deux groupes à laquelle il
va falloir remédier. Le choix de cette situation a été
fait afin que les élèves des deux groupes créent une
procédure de communication, en abandonnant l'écriture
chiffrée (qui pouvait également être faussée du fait
que certains élèves du groupe A ne savaient pas transposer la
quantité à l'écriture chiffrée), en abandonnant
l'oral, et en privilégiant le groupement.
La variable didactique qui influe énormément ici
est le nombre d'objets dans la collection qui est supérieur à 30,
c'est-à-dire supérieur à ce que les élèves
du groupe B connaissent, ce qui rend la tâche beaucoup plus fastidieuse
pour eux.
En effectuant cette expérience, les auteurs ont pu se
rendre compte que dans une situation où elles confrontaient des
élèves ayant une bonne connaissance du système
décimal (groupe A) à des élèves n'en ayant qu'une
connaissance minime (groupe B), les élèves de ce dernier groupe
ressentaient une frustration. Assurément, lorsque les
élèves comprennent qu'il y a un décalage entre ce qu'ils
savent et ce que les autres savent, ils se trouvent surpris de ne pas pouvoir
réaliser correctement la tâche, en comparaison avec leurs
camarades, surtout dans la petite classe qu'est le cours
préparatoire.

C'est en cela qu'une bonne compréhension, dès le
départ, du système de numération décimal,
permettrait de diminuer l'hétérogénéité
entre les élèves et le décalage de niveaux entre ces
derniers. Il serait idéal que les élèves aient le
même niveau de connaissance et que les apprentissages soient faits de la
même façon dans les classes, mais il ne s'agit que d'une
idéologie à laquelle il faut se confronter. Chaque
élève a son propre mode d'apprentissage et certains
élèves avancent plus vite que d'autres. Mais c'est
également cela qui engendre les lacunes des uns pendant que les autres
avancent.
Mais comment peut-on faire pour que les élèves
puissent se comprendre d'une façon simple et conventionnelle sans en
connaître trop de la numération ?
Dans cet article, l'expérience a pour objectif de
créer une stratégie de dénombrement identifiable par tous
sans avoir recours à l'écriture chiffrée (puisque non
décodable par tous les élèves) et d'abandonner le
dénombrement terme à terme. C'est à partir de là
que commence la base de la compréhension du système de
numération français.
On passe ici d'une situation de dénombrement à
une situation de communication écrite, dans le but d'avoir le nombre de
gommettes correspondant au nombre d'éléments de la collection. Le
fait que les élèves des groupes n'aient pas pu communiquer entre
eux a été un tremplin dans leur réflexion. Il est vrai
que, pour se comprendre, les élèves ont du élaborer une
stratégie n'utilisant ni l'écriture chiffrée, ni la
communication orale.
Cet article nous renseigne sur l'apprentissage d'une
écriture chiffrée du dénombrement qui amènera
ensuite à la compréhension de la numération grâce
aux groupements.
Mais il serait intéressant d'effectuer le même
genre d'expérience en utilisant les mots-nombres. On pourrait alors se
concentrer sur l'aspect oral du nombre et tenter de voir si cela peut aider les
élèves à comprendre notre système décimal
positionnel. Pour cela, les élèves n'auraient pas à
transmettre un bon de commande mais devraient directement demander à
voix haute le nombre de gommettes dont ils ont besoin. Cela amènerait
à la compréhension du sens de la numération grâce
à l'oralisation (exemple : si l'élève demande 52
gommettes, le mot « cinquante » pourrait faire sens si
l'élève

comprend qu'il s'agit de cinq dizaines et le mot « deux
» de deux unités, mais il s'agit d'une notion compliquée
surtout en classe de CP).
Grâce à la lecture d'un troisième article
de Hilli et Ruellan-Le-Coat (2009), dans lequel les auteurs provoquent le
dénombrement, le bon de commande est également mis en avant. Il
s'agit pour les élèves de dénombrer une quantité de
bougeoirs se trouvant sur un gâteau fictif (assiette en carton), afin de
passer commande du nombre de bougies correspondant à Freddy la
grenouille. Freddy est représentée par une marionnette mais elle
est sourde et ne sait lire que les chiffres de 1 à 9. C'est la
contrainte de l'expérimentation qui va faire que les
élèves n'auront pas d'autre choix que de réaliser des
groupements car le nombre de bougeoirs sera supérieur à 9.
Bien que la plupart des élèves n'y arrivent pas
du premier coup, l'obstacle de la surdité de la grenouille joue un
rôle très important puisqu'il bloque la demande orale des
élèves. En effet, si les élèves dénombrent,
par exemple, vingt-huit éléments dans la collection, la
grenouille lira 2 - 8 (« deux - huit ») et comprendra donc dix
éléments. Cet obstacle force les élèves à
chercher la stratégie de groupement, sans aucune aide de l'enseignant
(contrairement à l'article d'Aigoin et Guebourg (2004) où
l'enseignant faisait émerger l'idée de groupement lors d'une mise
en commun avec les élèves), et à élaborer une
situation de communication leur permettant d'obtenir le nombre de bougies
correspondant parfaitement au nombre de bougeoirs. Lors de cette
activité, la stratégie gagnante était en fait
d'additionner des paquets (inférieurs à 9) afin d'avoir le nombre
requis de bougies (exemple : pour 18 bougies, les élèves devaient
écrire 9, 9 sur leur bon de commande / pour 16 bougies, les
élèves pouvaient écrire 9, 7 ou alors 8, 6 etc.). Tous les
élèves ont trouvé la stratégie gagnante, certains
au bout de huit essais.
Dans ce même article, on relève l'activité
« Le grand Ziglotron » qui est une activité se
déroulant sur cinq séances et qui a pour objectif de
reconnaître la valeur positionnelle des chiffres dans l'écriture
des nombres en lien avec le groupement par dix.


Lors de la première séance, les
élèves doivent demander oralement le nombre de boutons qu'il leur
faut. L'enseignant précise bien qu'il existe des plaques de dix boutons
et que les élèves doivent demander le nombre exact de plaques de
dix boutons et de boutons isolés qu'il faut à leur Ziglotron.
La deuxième séance consiste en un travail
similaire, sauf que les élèves ne demandent plus oralement leurs
commandes mais doivent l'écrire sur le bon de commande ci-dessous :

Les autres séances seront explicitées dans la suite
de cette note de recherche.
Après lecture de ces trois articles, on peut
évidemment se rendre compte que les méthodes utilisées par
les différents auteurs font souvent appel à la communication (en
effet la façon dont on dit ou écrit les nombres est un code, une
convention qui ne devient nécessaire que lorsqu'on cherche à
exprimer une quantité pour quelqu'un d'autre que soi, et cette
communication repose surtout ici sur l'écriture en utilisant comme
contrainte l'interdiction de la communication orale. Grâce à cela,
j'aimerais pouvoir observer dans une classe si l'articulation entre l'oral et
l'écrit permettrait aux élèves de
mieux comprendre le sens de la numération
décimale. Voyons maintenant la place de la manipulation et du
matériel dans l'exécution de ces mêmes
expérimentations.
II. Le groupement par 10 et autres groupements
On a vu que le groupement par 10 était essentiel dans
la compréhension de la numération. Dans certaines
expérimentations que j'expliciterai ci-dessous, on remarquera que les
élèves n'arrivent pas souvent au déclic du groupement par
10 (probablement parce qu'ils ne le connaissent pas encore ou parce que le
calcul mental les en empêche ou encore parce qu'il n'y a pas de raison de
grouper par 10, puisqu'il faudrait d'abord avoir compris l'écriture et
la lecture du nombre) mais élaborent d'autres groupements.
En effet, les apprentissages de base de la numération
se font au cycle 2 (à partir du cours préparatoire) mais aussi
dès la maternelle. Les élèves apprennent à compter
jusqu'à 10, jusqu'à 20, jusqu'à 100 etc., mais ne se
rendent pas compte qu'ils abordent déjà le système
conventionnel de la numération consistant à organiser des paquets
de dix (dizaines), puis de dix paquets de dix (centaines) etc.
On peut également remarquer que l'apprentissage de la
numération à l'école se fait de dix en dix (exemple : on
apprend de 0 à 10, puis de 10 à 20 etc.) en utilisant la position
du nombre pour définir sa valeur (système positionnel). Le
système de groupement n'est pas un apprentissage en soi, mais c'est une
méthode qui permet de mieux comprendre et aborder notre système
de numération.
Les principales expérimentations du groupement se font
en poussant les élèves à trouver d'eux-mêmes une
stratégie efficace. Les enseignants cherchent à amener les
élèves à grouper, de façon aléatoire ou
irrégulière pour aller vers le groupement par dix.
Effectivement, c'est grâce à une pédagogie
constructiviste que l'élève, lors d'une situation
problème, va pouvoir renforcer ses connaissances. C'est en cela qu'il
faut les laisser élaborer des stratégies, les laisser
réfléchir ou trouver eux-mêmes la solution, qui ne sera pas
souvent le groupement par 10

La deuxième expérience de l'article d'Aigoin et
Guebourg (2004) a eu lieu le même jour et consistait en un échange
des rôles entre les deux groupes, c'est-à-dire que le groupe A
devient récepteur du bon de commande que le groupe B aura
élaboré (les élèves du groupe A sont toujours ceux
qui ont une bonne connaissance de la comptine numérique et associe le
mot nombre à son écriture chiffrée et le groupe B sont les
élèves qui connaissent la comptine jusqu'à 30 et
au-delà mais n'associent pas le mot nombre à son écriture
chiffrée).
On peut remarquer que lors de la deuxième
expérience, les élèves du groupe B, qui ont chacun le
même nombre d'éléments à dénombrer, ont fait
des tentatives de stratégies (telles que le marquage des
éléments lorsqu'il est compté par exemple), mais ont tout
de même compris le sens de la communication dans cette situation. Voulant
absolument transmettre leurs messages aux élèves du groupe A, ils
ont fini par grouper de façon irrégulière parfois
(groupements différents : 2/5/6/4) ou de façon
régulière (exemple : groupement par 11).
La stratégie de groupement remplace le
dénombrement terme à terme et permet donc à
l'élève un gain de temps et un apport cognitif pour la suite de
la compréhension de la numération. Les expérimentations
pour amener cette stratégie se font principalement sur de grandes
collections à dénombrer (au-delà de la comptine
numérique qu'ils connaissent) pour que les élèves laissent
de côté le dénombrement unitaire.
Dans cet article (Aigoin & Guebourg, 2004), on peut noter
que le souhait du groupement par dix n'a pas abouti mais cette situation
problème a mis les élèves dans une réflexion
complexe.
Les auteurs ont cherché, grâce à leur
expérimentation, à ce que les élèves créent
une stratégie de groupements irréguliers (exemple : 3/3/4/5) qui
ne seront pas évidents à additionner, afin de les amener aux
groupements par dix (plus simple à appréhender si leurs
capacités en calcul mental le permettent).
Hilli et Ruellan-Le-Coat (2009) nous renseigne sur
l'apprentissage de la régularité des groupements. Les auteurs,
grâce à une expérimentation faite en classe de CP vont
amener les élèves à grouper de façon
irrégulière pour arriver aux groupements par dix.

Lors d'une phase d'institutionnalisation (c'est la phase
où l'on généralise une connaissance) les auteurs disent
que : « pour dénombrer une collection, il n'est pas
nécessaire de compter un à un tous les éléments de
la collection, on peut aussi dénombrer séparément autant
de petits paquets que l'on veut. »
Les groupements sont souvent provoqués par les
enseignants qui choisissent des expérimentations contraignantes pour
obliger les élèves à les utiliser, mais ces derniers n'ont
pas directement l'automatisme de choisir le groupement par 10.
III. La manipulation et le matériel
Dans l'article de Bednarz et Janvier (1984), on peut relever
la difficulté que le matériel (ou dessins) utilisé dans
l'enseignement est essentiellement utilisé à des fins
d'écriture : les élèves ne voient pas la véritable
représentation du matériel en terme de groupements. Il s'agit
d'un élément intéressant puisque le matériel,
censé symboliser les groupements, n'a pas forcément de sens pour
les élèves lors de cette expérimentation.
Les auteurs notent également que la manipulation de
matériel est conçue en fonction d'un travail sur
l'écriture : le matériel ne joue pas le rôle de support
qu'il doit jouer. Ici, le passage entre quantité et nombre écrit
est questionné puisque la manipulation permet de faire comprendre aux
élèves qu'on fait des paquets de 10 (par économie et
efficacité) et que l'on écrit ensuite ces différents
paquets d'une certaine façon afin de créer un nombre
(numération décimale de position).
Le matériel doit être perçu comme un
véritable support afin que les élèves puissent
eux-mêmes s'en servir dans la résolution de problèmes. Ils
doivent pouvoir se l'approprier et en déchiffrer le sens pour pouvoir
l'utiliser à des fins de compréhension.
Dans l'article de Hilli et Ruellan-Le-Coat (2009), la
manipulation et le matériel sont deux variables extrêmement
importantes. La disposition spatiale des bougeoirs constitue une aide ou non
pour l'élève lors de la réalisation de la tâche. En
effet, si les bougeoirs sont alignés, l'élève aura
tendance à utiliser cet alignement pour transposer le nombre de bougies
par ligne.
1
3
2
5
3
Ici, l'élève aura tendance à donner les
groupements qu'il voit, ce qui facilite la création de groupements
irréguliers (1/3/2/5/3).
En revanche, si les bougies sont disposées de
façon aléatoire sur l'assiette en carton, l'élève
n'aura pas d'aide et il devra comprendre par lui-même qu'il faut faire
des groupements afin de passer commande à Freddy.
Dans cette expérimentation, plusieurs phases ont
été mises en place dans la séance afin de remédier
aux difficultés des élèves. Au cours de la deuxième
phase (situation problème en binôme), l'enseignant a
autorisé les élèves à déplacer les bougeoirs
s'ils en avaient besoin.
Pour les élèves, il est important de
déplacer les éléments qu'ils manipulent, afin de rendre la
situation plus concrète. Ici, on peut imaginer par exemple que certains
élèves déplaçaient les bougeoirs qu'ils comptaient
ou les rapprochaient pour symboliser des groupements.
On peut également relever grâce à cet
article qu'il est extrêmement attractif pour les élèves de
manipuler des objets qu'ils ont l'habitude de voir ou d'utiliser. Ici, Freddy
la grenouille est représentée par une marionnette, symbolisant la
sympathie et l'amusement. Lors de cette expérience, les
élèves doivent compléter des bougies sur un gâteau
d'anniversaire, qui est assimilé à la fête et au plaisir.
Aussi, les élèves savent qu'ils ont un but précis qui est
de remplir le gâteau, ce qui va les stimuler et les aider à
être rapides. Il faut utiliser des objets attrayants pour les enfants,
leur permettant de rendre la situation concrète et amusante, ce qui va
également permettre une entrée rapide dans l'activité. Si
les élèves s'ennuient ou ne sont pas stimulés,
l'activité va être lente et sans but d'apprentissage pour eux. Il
est logique de souligner que les enfants

retiennent plus facilement ce qu'ils ont
apprécié que ce qui les a ennuyés. Il vaut mieux
privilégier des activités ludiques dans lesquelles l'enfant se
sentira impliqué ; cela jouera un rôle sur l'intérêt
qu'il portera à ces activités mais sous-entendra également
que l'enfant assimilera mieux les apprentissages qui influeront sur sa
réussite scolaire.
La manipulation de matériel est une étape
clé qui entraîne l'écriture positionnelle. Elle est donc
importante et les enseignants ont tendance à croire que les
élèves assimilent le passage entre ces deux étapes de
façon aisée. Il faudrait donc passer plus de temps à faire
comprendre aux élèves que l'étape de la symbolisation des
groupements grâce à la manipulation permet l'écriture et,
avec quelques irrégularités, la lecture. Les enseignants
gagneraient à accentuer le lien qu'il existe entre ces deux actes.
Dans cet article est également explicitée la
troisième séance du « Grand Ziglotron ». Lors de la
troisième séance, ce n'est plus aux élèves de
dénombrer les boutons mais à l'enseignant. Ce dernier remplit la
première phrase du bon de commande « Il me faut É boutons,
je commande : » et c'est aux élèves de remplir le reste.
C'est un travail individuel et un apprentissage clé puisque les
élèves n'ont plus de matériel à disposition et se
concentrent uniquement sur l'écriture et les groupements de dix dans le
nombre écrit. L'absence de matériel va obliger
l'élève à une certaine réflexion face à sa
situation problème et l'on peut remarquer grâce à cela que
le matériel constitue une aide indispensable dans la symbolisation d'une
situation de groupements.
Ces deux articles nous permettent de remarquer l'importance du
matériel à utiliser lors d'expérimentations liées
au groupement et l'importance de la manipulation des élèves.
Cette dernière aidera l'élève à donner plus de sens
à la situation et cela facilitera sa compréhension.
IV. Le groupement en lien avec les
opérations
Lors de l'apprentissage des différentes
opérations, les élèves ne font pas appel aux groupements.
En effet, l'apprentissage de la numération est détaché de
celui des opérations.

Si les élèves ont appris la numération de
façon à ce qu'elle ait du sens, ils doivent automatiquement
pouvoir faire le lien certaines opérations. Lors de l'apprentissage de
l'addition (posée ou en ligne), les élèves doivent
comprendre qu'ils associent des unités entre elles, des dizaines entre
elles
etc. et qu'ils ne peuvent pas associer une
centaine avec une unité par exemple. Cela fait partie des règles
de l'addition
Exemple :
1 1
Dans cette addition, on a additionné les unités
ensemble (5+8), les dizaines ensembles (7+2+1(retenue)) et les
centaines ensembles (1+2+1(retenue)). On n'aurait pas pu
additionner le 1 de 125 avec le 8 de 278. Dans l'apprentissage de l'addition,
les élèves doivent savoir que les groupements s'additionnent et
s'échangent entre eux.
Aussi, l'apprentissage des groupements prend tout son sens
lors des retenues. En effet, lorsque l'on addition 8 et 5, cela donne 13. Le
chiffre 13 étant décomposé en une dizaine et trois
unités, on décale la dizaine obtenue au rang des dizaines pour
pouvoir l'inclure dans l'opération. C'est exactement le même
principe pour les dizaines transformées en centaines.
Le sens de la numération décimale a tout son
sens dans les opérations et lorsqu'elle est comprise, elle permet aux
élèves de comprendre l'utilité des groupements et les
règles qui y sont associées.
Pour la soustraction, il s'agit du même principe que
pour l'addition. En effet, lorsque l'on soustraie deux nombres, on doit
soustraire chaque groupement ensemble.
Exemple :
2 1 13 6

- 5 3
1 8 3
Le principe est le même. En effet, 3 Ð 8 n'est pas
une soustraction faisable. On va donc « casser » une centaine pour la
transformer en dix dizaines et pouvoir soustraire les dizaines ensembles. Il
s'agit là d'une méthode de soustraction parmi une multitude
d'autres.
Concernant la multiplication posée, on ne fait pas
intervenir les mêmes règles que pour l'addition et la
soustraction, mais il s'agit tout de même d'une opération de
groupements.
Prenons l'exemple d'un problème multiplicatif tel que :
« Dix élèves disposent de 4 billes chacun.
Combien ont-ils de billes au total ? »
Ici, les élèves peuvent utiliser l'addition
réitérée relative à la multiplication
(4+4+4+4+4+4+4+4+4+4 ou encore 10+10+10+10). Il s'agit là d'additionner
des groupements et d'utiliser des chiffres adéquats afin que
l'élève puisse réfléchir à la
stratégie la plus efficace pour résoudre son problème. Il
semblerait que l'addition de 10+10+10+10 serait la plus judicieuse et la plus
utile en termes de groupements décimaux.
Le groupement permet également de comprendre la
division, puisque contrairement à la multiplication, il s'agit d'une
méthode de partage.
Exemple :
« Avec 40 gâteaux, on fait des paquets de 10
gâteaux. Combien peut-on faire de paquets ? »
Dans cette situation aussi, l'élève va utiliser
des groupements en partageant.
Dans les opérations, on regroupe les nombres afin de
résoudre des problèmes. L'addition et la soustraction font
directement référence aux groupements décimaux car il y a
des règles qui s'y conforment et qui obligent à additionner ou
soustraire les différents groupements entre eux. La multiplication ou la
division ne font pas
directement appel aux groupements décimaux mais font
tout de même référence aux notions de groupements. Elles
peuvent très bien être utilisées à des fins
d'apprentissages de la numération ou en guise d'introduction lors de
l'apprentissage des groupements décimaux. Le choix des nombres doit tout
de même être pertinent afin que les élèves puissent
comprendre que cela va les amener aux groupements décimaux.
On peut également utiliser du matériel afin
d'apprendre les opérations (exemple : cubes, plaquettes de dix etc.
É). Ce matériel sert à structurer les apprentissages des
élèves, dans le sens où ils peuvent manipuler pour
comprendre. En effet, différents matériels peuvent servir
à associer des termes qui feront l'objet d'opération.
Aussi, les opérations peuvent se trouver parfois
directement dans la numération orale. On associe deux termes oraux qui
traduisent clairement une opération :
Exemples : vingt-et-un signifie vingt plus un (addition)
Quatre-vingt signifie quatre fois vingt (multiplication)
Cela montre qu'il existe un lien fort entre nombre et
opération. Ce lien passe en particulier par l'importance des groupements
par dix.

~ 28 ~
Synthèse
On a pu voir à quel point la numération
était un domaine important lors des apprentissages fondamentaux des
élèves. En effet, ce thème fait partie intégrante
des savoirs indispensables que l'école doit pouvoir transmettre à
ses élèves. Chaque enseignement doit être compris par les
élèves et doit être amené de façon à
ce qu'il ait du sens. C'est la grande difficulté de l'école.
Afin que les élèves puissent avoir une
compréhension optimale de la numération, on a pu voir que les
enseignants, les programmes et les manuels mettaient en place des aides
à cette assimilation. En effet, la stratégie de groupement
constitue un véritable tremplin pour que l'élève puisse
donner du sens à notre système positionnel de numération
décimale.
Grâce à la lecture de différents articles
et aux apports directement prélevés en classe, j'ai pu constater
qu'il existait différentes techniques concernant le groupement, pouvant
permettre à l'élève de comprendre la numération
dans son sens le plus profond.
Certains privilégient les méthodes de
groupements à l'écrit, qui vont permettre de mettre en avant une
organisation spatiale qui fera sens au dénombrement (exemple :
bâtonnets) mais ne pourra pas être transposée
automatiquement à l'écriture chiffrée (Cf. disposition
spatiale de Hilli et Ruellan-Le-Coat). En effet, les apprentissages de
l'écriture chiffrée au cours préparatoire peuvent toujours
entraîner des erreurs de la part des élèves. Lors d'un
dénombrement et afin d'être compris par tous les
élèves de la classe, quel que soit leur niveau, les
élèves vont être amenés à grouper pour
communiquer de façon écrite. Cela passe souvent à travers
l'élaboration d'un bon de commande. Favoriser le groupement dans
l'écriture va également permettre aux élèves de
comprendre le sens de l'écriture chiffrée du système
positionnel français. En effet, grâce à une première
symbolisation écrite, les élèves vont pouvoir
appréhender les notions d'unités, dizaines, centaines, et
comprendre la position d'un chiffre dans un nombre.
D'autres vont privilégier l'absence de l'oral («
Freddy la grenouille ») qui va obliger l'élève à
trouver une autre stratégie de communication (sous entendue
l'écrit). Dans les articles que j'ai pu lire, l'oral n'est pas toujours
mis en avant. Il serait intéressant, lors d'une éventuelle
recherche, de s'attarder sur l'aspect oral des nombres et sur le sens qu'il
peut transmettre. En effet, les nombres sont constitués
généralement grâce aux groupements auxquels ils
appartiennent, mais dans le système français, il existe
énormément d'exceptions des mots-nombres pouvant engendrer une
difficulté de compréhension du système en lui-même
par les élèves (exemple : le mot « dix-sept » peut
être perçu comme une dizaine et sept unités par les
élèves, après un apprentissage. Mais le mot « douze
» ne peut pas être associé facilement à une dizaine et
deux unités.). L'apprentissage de la numération à travers
les groupements oraux me semble être plus difficile que l'écrit
à transmettre aux élèves, bien qu'il soit très
intéressant.
La symbolisation des groupements par les objets et la
manipulation sont des atouts majeurs dans la compréhension de la
numération. Il est en vrai que c'est en manipulant que les
élèves arrivent à donner du sens à leurs
apprentissages. Utiliser du matériel et privilégier la
manipulation va rendre la situation plus concrète. Mais attention, il ne
s'agit pas juste de manipuler des objets et de passer ensuite aux groupements.
Manipuler ces objets doit permettre de faire un lien avec les groupements. Les
enseignants doivent faire comprendre aux élèves que le but de la
symbolisation grâce au matériel est la compréhension de
l'écriture décimale des nombres (exemple : si
l'élève manipule 10 paquets de 3, ils symboliseront trois
dizaines). La manipulation permet de rendre une situation réelle et est
très importante puisqu'elle permettra une meilleure compréhension
si le lien entre celle-ci et l'écriture des nombres est bien fait. On ne
doit pas seulement manipuler pour écrire, on doit manipuler pour donner
du sens et écrire grâce à ce que l'on a compris de la
manipulation.
Lors des expériences, les auteurs des différents
textes ont parfois provoqué le groupement ou ont laissé
l'élève choisir seul sa stratégie. C'est lorsque
l'élève tâtonne afin de trouver une stratégie qu'il
va offrir plusieurs possibilités de réponses à sa
situation problème. Les auteurs ont voulu faire émerger la
stratégie de groupement par les élèves, sans pour autant
s'être attardés sur l'aspect numéral de ces groupements. En
effet, les expériences ont permis aux élèves de
créer des groupements, mais pas souvent

des groupements de 10. Il ne s'agit pas de quelque chose de
très grave, puisque, par la suite, les enseignants pourront aider les
élèves à comprendre que la stratégie de groupements
par 10 est la plus simple à utiliser. Il est vrai que l'enseignant doit
faire comprendre aux élèves que créer des groupements
irréguliers (tels que 3-5-7-9-2) ne va pas permettre une addition
facile. De plus, il est plus utile que les élèves comprennent que
créer des groupements de même quantité va leur permettre de
comparer deux quantités très rapidement (exemple : cinq
groupements de dix d'un côté, quatre groupements de dix de l'autre
; on peut repérer directement qui en a le plus). En revanche, si l'on
regroupe par 10, on pourra, grâce à la comptine numérique,
aux calculs ou encore aux apprentissages de 10 en 10, prouver aux
élèves qu'il est plus stratégique d'effectuer des
groupements de 10, bien qu'à ce stade de l'apprentissage de la
numération, ils pourront préférer d'autres
stratégies (2 en 2, 20 en 20). La capacité du groupement n'est
pas très importante puisqu'elle permet tout de même aux
élèves de grouper et cela constituera une bonne introduction pour
la numération décimale.
Bien que la numération et les opérations soient
deux apprentissages différents, ils peuvent et doivent être
reliés entre eux. C'est grâce à cela que les
élèves comprendront le véritable sens des
opérations dès le plus jeune âge. En effet, pour les quatre
opérations, on a recours à la notion de groupement. L'addition et
la soustraction étant les deux opérations ayant des règles
de groupements décimaux, il est important pour les élèves
de comprendre pourquoi on additionne (ou soustrait) tel chiffre avec tel
chiffre. Les problèmes de multiplication et de division font
également appel aux groupements, mais les groupements semblent moins
évidents puisque moins visibles directement lors de
l'opération.

~ 31 ~
Problématique et hypothèse
I. Présentation de la problématique
Après lecture et analyse de ces différents
articles, j'ai pu me rendre compte qu'il fallait une articulation de plusieurs
techniques, faisant appel à l'oral, à l'écrit, à la
manipulation et au sens tout en faisant émerger la stratégie du
groupement par l'élève lui-même, afin qu'il puisse
être à même de comprendre le système français
de numération décimal de façon complète.
L'utilisation de tous ces moyens simultanément me
semble être quelque chose de trop complexe. M'intéresser à
la confrontation parallèle de deux moyens me semble être un choix
plus judicieux.
En outre, je peux me poser le problème suivant :
L'articulation de l'oral et de l'écrit dans une méthode
mettant en place l'élaboration du groupement par 10, permettrait-elle
une meilleure compréhension de notre système français de
numération décimale ?
II. Hypothèse
Dans le but de répondre à cette
problématique, je peux en amont émettre l'hypothèse
qu'utiliser une méthode dans laquelle l'élève serait
amené à articuler l'oral et l'écrit, dans le but de faire
émerger la notion de groupement par 10, permettrait de donner un sens au
système français de numération. Le fait que
l'élève puisse y donner du sens entrainera, par
conséquent, une meilleure compréhension de ce système.
Afin de tester cette hypothèse, je dois mettre en place
un protocole expérimental me permettant de l'infirmer ou de la
confirmer.
~ 32 ~
L'expérimentation
Une année de stage est mise en place en deuxième
année de Master, me permettant, entre autre, de pouvoir mettre en place
une expérimentation répondant à ma problématique.
Cette expérimentation sera effective si elle est menée dans une
classe de CP. Elle pourra être repensée s'il s'agit d'une classe
de CE1 mais ne pourra pas être efficace dans un niveau
supérieur.
I. Le choix de l'expérimentation
Ma problématique étant de savoir si
l'articulation entre l'oral et l'écrit permet une meilleure
compréhension du système décimal de numération, je
me suis demandée quelle expérimentation je pouvais mettre en
place pour pouvoir y répondre.
Lors de mes lectures d'articles, je me suis
intéressée à la compréhension de la valeur
positionnelle des chiffres dans les nombres pour pouvoir comprendre la
numération. En effet, puisque les élèves de la classe de
CP dans laquelle je vais mener mon expérimentation, n'ont qu'une faible
(voire aucune) connaissance au niveau des groupements (par dix) et au niveau du
sens des dizaines et des unités, je me suis dit qu'il fallait commencer
par une compréhension de la valeur positionnelle des chiffres pour
comprendre la numération et le sens du nombre par la suite.
Aussi, il convenait que je puisse mêler l'oral et
l'écrit dans une expérimentation pour mettre en avant le
principal aspect de ma problématique.
La notion mathématique visée dans cette
séquence est l'apprentissage de la numération, ou plus
particulièrement la compréhension profonde de notre
système décimal de numération. En effet, la plus grande
difficulté que les élèves ont lors de l'apprentissage de
la numération est d'en comprendre son sens, de savoir pour quelles
raisons on utilise ce système de position et de comprendre comment il
fonctionne.
Grâce à l'article d'Aigoin et Guebourg (Du
dénombrement terme à terme aux groupements réguliers : un
pas nécessaire vers la compréhension de notre système de
numération positionnelle, 2004), je me suis
intéressée à la situation du Grand Ziglotron (Cap Maths,
Hatier, 2009) qui permet de comprendre et d'utiliser la valeur positionnelle
des chiffres dans un nombre grâce, entre autre, à la formation de
groupements de dix.
Cette situation m'a parue pertinente à mettre en place
en classe car en même temps d'être ludique, elle permet
différentes modalités de travail : groupes et individuel. Elle
m'a également semblée adéquate, puisque l'on peut la
travailler en utilisant d'autres exercices oraux en parallèle, qui
serviront à appuyer l'activité et à approfondir les
connaissances des élèves. Effectivement, pour trouver une
situation en lien avec ma problématique, je me dois de mêler
l'écrit et l'oral afin de savoir si cela permet une meilleure
compréhension de la numération.
Pour ces raisons, j'ai choisi de mettre en place la situation
du Grand Ziglotron, dans une classe de CP comptant 21 élèves. Le
choix du niveau était presque obligatoire, puisque c'est à ce
stade de leur scolarité que les élèves commencent à
apprendre la numération sous forme de dizaines et d'unités et
à ce niveau que mon expérimentation pourra être effective.
Aussi, ils n'ont que très peu de connaissances quant au sens de la
numération et à la formation des nombres. On aurait pu mener
cette expérimentation en classe de CE1 et l'adapter ou vérifier
si une méthode d'apprentissage travaillée en CP aurait permit des
facilités d'apprentissage.
La situation du Grand Ziglotron, telle qu'elle est
décrite dans le manuel Cap Maths, est composée de cinq
séances. Or, j'ai choisi de mener une expérimentation de cinq
séances au total, dont trois proviennent du Grand Ziglotron,
combinées à d'autres activités orales, et deux qui
serviront à l'évaluation diagnostique et à
l'évaluation finale.
~ 33 ~
II. Le déroulement de la séquence
'-' 34 '-'
Dans cette séquence de cinq séances, les
élèves sont amenés à grouper par dix dans le but
d'appréhender plus clairement le système décimal de
numération française. Ils ont pour consigne de devoir remplir un
robot électronique (le Grand Ziglotron) qui ne peut fonctionner que
lorsque tous ses boutons sont complétés.
Comme il est indiqué ci-dessus, j'ai fais le choix de
n'utiliser que trois séances de cette situation : il s'agit des
séances 1, 2 et 3. Ces trois séances sont, selon moi, les plus
intéressantes puisqu'elles proposent des situations et manipulations
différentes, qui permettront aux élèves de diversifier
leurs procédures (les séances 4 et 5 du manuel Cap Maths sont des
séances d'entraînement et d'évaluation). Aussi, les trois
situations choisies sont assez courtes pour être associées
à des exercices oraux (par exemple, un travail sur l'ardoise), ce qui me
permettra de répondre à ma problématique en combinant les
deux modalités de travail (écrit et oral).
Ci-dessous je présenterai le déroulement des
cinq séances, ainsi que les analyses à priori de celles-ci.
III. Présentation des cinq séances
Séance 1
J'ai choisi d'effectuer un test diagnostic, qui servira
à repérer les conceptions des élèves en ce qui
concerne la numération, mais également leur capacité
à mettre en relation différentes écritures d'un nombre
dans différents systèmes de représentations
sémiotiques (exemple : système positionnel, décimal, par
unité d'ordre donné...).
Ce test diagnostic aura pour but de dénombrer un nombre
de billes qu'il y a sur une feuille (trois séries à
dénombrer), et d'écrire le nombre sous la forme du système
positionnel (exemple : 26) et sous la forme d'unités, dizaines (exemple
: 2 dizaines, 6 unités).
Ici, il est clair que toutes les évaluations
diagnostiques des élèves seront recueillies. Lors de cette
séance, il sera également judicieux de s'intéresser aux
procédures des élèves pour dénombrer (barrer,
colorier, entourer des paquets...).
'-' 35 '-'
Je soulignerai aux élèves le fait qu'ils ne
devront pas gommer ce qu'ils ont fait afin de pouvoir recueillir
différentes procédures directement sur le test.
Cette évaluation sera entièrement autonome et je
laisserai les élèves libres de toute procédure.
Les données à recueillir :
Dans cette première séance, je
m'intéresserai beaucoup aux procédures des élèves
pour dénombrer. J'utiliserai alors une grille d'analyse dans laquelle je
noterai les différentes stratégies qu'ils mettront en place.
Il sera également intéressant de relever le
temps d'exécution des élèves, afin de souligner si
certains élèves ont des facilités ou des
difficultés dans la réalisation de cette évaluation.
Les résultats des élèves seront
classés en fonction de leur justesse et de leur cohérence.
Séance 2
C'est lors de la deuxième séance que se fera la
présentation de la situation. Les élèves seront face
à une situation problème leur permettant un apprentissage
constructiviste.
Divisés en équipes de deux ou trois (acheteurs),
ils devront mettre en place une procédure de leurs choix, afin de
demander le nombre exact de boutons pour remplir le Ziglotron à un
marchand (trois marchands ayant un bon niveau en numération seront
désignés au préalable). Ce travail se fera à
l'oral.
L'enseignant devra préciser que les boutons sont
répartis en plaques de dix ou à l'unité.
L'élève devra demander un nombre de plaques, de boutons, ou
encore de plaques et de boutons au marchand. Cette phase permet l'appropriation
de la situation par les élèves mais également
l'observation de la diversité des procédures qu'ils vont mettre
en oeuvre.
L'acheteur validera ensuite le nombre de boutons en
remplissant le Ziglotron. Il est évident que l'on devra vérifier
le nombre de boutons que donnera le marchand à l'acheteur, afin de voir
s'il correspond à ce qui sera demandé.
Une phase de mise en commun sera ensuite établie afin
de connaître les procédures choisies, ce que les acheteurs ont
demandé aux marchands et si le groupe a réussi ou
échoué.
Une synthèse conclura cette séance dans laquelle
nous reviendrons sur les procédures valables ou non des
élèves et sur les procédures les plus stratégiques
selon eux.
Les données à recueillir :
Dans cette séance, je recueillerai les
procédures des élèves pour dénombrer (grâce
à une grille d'observation), les désaccords entre eux s'il y en
a, la façon dont ils demandent aux marchands (exemple : 26 boutons ou 2
plaquettes de 10 et 6 boutons seuls), la façon dont les marchands
comptent (plaquettes de 10 + boutons isolés ou boutons isolés
uniquement).
Aussi, je m'intéresserai à savoir si les
élèves ont eu trop de boutons en leur précisant de laisser
les boutons en trop au coin de la table (grâce à leurs Ziglotrons,
je pourrai relever les élèves ayant eu un nombre exact de boutons
et ceux n'en ayant pas eu assez).
Enfin, la fiche du Grand Ziglotron servira, à
vérifier la compréhension et la justesse de la tâche. Cette
fiche servira surtout à savoir si les élèves
dénombrement correctement ou s'ils ont des difficultés.
Séance 3
La troisième séance présentera la même
activité avec quatre contraintes majeures :
- Les acheteurs devront transmettre un bon de commande aux
marchands. - Ils ne pourront pas communiquer entre eux.
'-' 37 '-'
- Les marchands ne pourront pas donner plus de neuf boutons
isolés.
- Les élèves ne devront pas coller les boutons
sans que l'enseignant juge de leur réussite.
Cette séance oblige les élèves à
prendre en considération le groupement par 10.
Une phase de mise en commun permettra de juger de la
lisibilité des bons de commande et de leur conformité aux
contraintes, de vérifier la pertinence de la répartition des
boutons dans les bons de commande, et de chercher l'origine des erreurs s'il y
en a.
Une troisième phase de la séance offrira un
entraînement collectif aux élèves à travers l'oral.
On demandera combien de plaques et de boutons il faudra pour un nombre de
boutons donné et inversement. Les élèves écriront
alors les réponses sur leurs ardoises et l'on recueillera les
différentes erreurs pour les exploiter.
A la fin de cette séance, une institutionnalisation
aura lieu sur le fait que les plaques de dix représentent les dizaines
et les boutons isolés, les unités. Ainsi, l'élève
pourra acquérir le vocabulaire associé aux nombres en ayant
d'abord travaillé sur son sens.
Les données à recueillir :
Dans cette séance, je recueillerai les bons de commande
des élèves, ainsi que leurs justifications orales, afin de
comprendre comment s'est fait le cheminement de leurs réponses. Cela
permettra également de souligner, à ce stade de
l'expérimentation, si des difficultés persistent au niveau de la
compréhension de la situation et ainsi, de les exploiter pour les
éclaircir.
Ici, je m'intéresserai également aux discussions
internes des groupes - car les élèves sont toujours par deux ou
trois - afin de voir s'ils échangent ou non leurs procédures et
s'ils arrivent à se mettre d'accord.
Grâce à une grille d'observation, je
relèverai également les résultats des élèves
quant au travail sur ardoise (erreurs, justifications, bons résultats
etc. )
Séance 4
La séance 4 est identique à la troisième,
hormis le fait que les élèves n'ont plus le Ziglotron à
leur disposition. C'est l'enseignant qui en disposera et qui aura remplit au
préalable la première partie du bon de commande (« Il faut
É boutons »).
Les élèves devront remplir la suite du bon de
commande. Cette résolution se fera de façon individuelle. Cette
séance permet aux élèves de faire directement le lien
entre l'écriture et le groupement par 10 puisque le matériel
n'est plus à disposition des élèves. Cela va donc
permettre de tester leur capacité à avoir institutionnaliser la
tâche, sans avoir recours au matériel.
Une phase de mise en commun et de synthèse est ensuite
mise en place, dans laquelle nous ferons le tri entre les réponses des
élèves (bonnes ou mauvaises) et expliquerons pourquoi. Nous
ferons ressortir les procédures mises en oeuvre et nous
établirons une synthèses des procédures efficaces.
Lors d'une dernière phase, les élèves
devront répondre au même exercice oral que la séance 3 sur
leurs ardoises, mais ne devront plus utiliser les mots « paquets de dix
» et « boutons isolés », mais dizaines et unités
(ou d et u).
Les données à recueillir :
Lors de cette séance, les données recueillies
seront semblables à celles de la séance 3, mais je
m'intéresserai tout particulièrement aux procédures des
élèves dans la résolution de la tâche. En effet,
comme les élèves devront identifier le nombre, et le
décomposer sous formes de paquets de dix boutons et de boutons
isolés, sans avoir aucun matériel à leur disposition, le
travail sera sans doute plus laborieux.
Une feuille de brouillon sera distribuée à tous
les élèves pour qu'ils puissent écrire le cheminement de
leur réflexion.
Séance 5

~ 39 ~
La cinquième séance concernera
l'évaluation finale à travers laquelle les élèves
devront refaire l'évaluation diagnostique donnée lors de la
première séance. Cette trace écrite permettra alors de
relever les difficultés persistantes ou justement, de repérer les
bienfaits de l'expérimentation à travers les évolutions
des élèves.
Les données à recueillir :
Ce sont les mêmes que lors de la séance 1.
Analyse
I. Analyse a priori
Afin de mener au mieux cette expérimentation et de
réagir au plus vite face aux difficultés des
élèves, je me dois d'effectuer une analyse a priori des
différentes séances présentées ci-dessus.
Après un court entretien avec l'enseignant responsable de cette classe,
j'ai pu apprendre qu'il s'agissait d'une classe de vingt-et-un
élèves ayant un niveau global moyen. En numération, et
tout particulièrement dans le domaine des groupements dizaines et
unités, les élèves n'ont aucune connaissance et
l'enseignant était sur le point de travailler cela avec eux. Cette
information est importante puisque c'est grâce à
l'expérimentation que je vais mener que les savoirs vont se mettre en
place.
Séance 1
Lors de la première séance, qui est celle de
l'évaluation diagnostique, les élèves pourront utiliser
plusieurs procédures. En effet, l'objectif de cette évaluation
étant de dénombrer un nombre de billes donné et d'en
écrire la quantité (sous deux écritures : nombre total de
billes et nombre de dizaines et d'unités), ils vont pouvoir
dénombrer de différentes façons :
- en barrant les billes déjà comptées
(trait ou croix) - en mettant un point dans chaque bille
dénombrée
- en créant des paquets (d'un nombre de billes qu'ils
choisiront eux-mêmes) - en dénombrant visuellement ou avec leur
doigt
Parmi ces procédures, il y en a qui peuvent conduire
à des erreurs de dénombrement. En effet, créer des paquets
réguliers ou non peut induire l'élève en erreur lorsqu'il
devra les additionner.
Aussi, dénombrer visuellement ou avec le doigt peut
mener à des oublis ou au surcomptage.
Ces procédures sont d'autant plus sujettes à
erreurs si l'élève y associe des pauses (lors du
dénombrement) ou s'il manque de concentration. Je pourrai relever cela
en observant les élèves et surtout en passant dans les rangs pour
vérifier de leur concentration. Si je remarque des groupes faisant autre
chose, je ne manquerai pas de leur rappeler ce qu'ils doivent faire.
En revanche, lorsque les élèves vont barrer ou
mettre un point dans une bille, les possibilités d'erreurs de
dénombrement seront plus faibles, puisqu'en « pointant »
chaque objet, il pourra les compter au fur et à mesure, et éviter
les oublis. Dans ces procédures, l'élève pourra aussi
faire des erreurs s'il manque de concentration.
Dans cette évaluation, les consignes étant
expliquées au préalable, l'élève ne devrait pas
avoir de difficultés lors de la compréhension de celles-ci,
puisque très simples (« Ecris le nombre de billes qu'il y a
»).
C'est lorsqu'il devra faire le rapport entre le nombre de
billes et le nombre de dizaines et d'unités que les difficultés
se ressentiront. En effet, les élèves n'ayant presque aucune
connaissance en matière de dizaines et d'unités, les
résultats seront inscrits selon différentes stratégies
:
- au hasard (l'élève inscrit des chiffres au
hasard là où il y a des pointillés puisqu'il ne fait aucun
lien entre les différentes écritures du nombre)
- en utilisant les mêmes chiffres que
précédemment (exemple : si le nombre de billes est de 26,
l'élève utilisera les chiffres 2 et 6 pour les inscrire sur les
pointillés)

- de façon juste (l'élève aura
connaissance de la dizaine et de l'unité et comprendra alors le lien
entre les deux écritures).
Dans cette évaluation, l'élève pourra
alors faire deux types d'erreurs qui seront celles lors du dénombrement,
ou celles lors de l'écriture du nombre de dizaines et d'unités.
N'ayant pas connaissance du niveau de ces élèves, je ne saurai
dire s'il y aura des erreurs lors de l'écriture même des chiffres
ou de confusion entre certains chiffres. Les nombres écrits à
l'envers ou d'une mauvaise façon ne sera pas une erreur à prendre
en compte lors de cette évaluation.
Séance 2
Dans cette séance, qui a pour objectif l'appropriation
de la situation par tous, les élèves par équipes de deux
ou trois devront dénombrer le nombre de boutons manquants au Ziglotron
et demander aux marchands de lui donner le nombre de boutons correspondant.
Dans cette séance les procédures et erreurs des
élèves peuvent être nombreuses, puisqu'il s'agit d'une
séance de découverte.
La consigne, étant explicitée par l'enseignante
et réexpliquée par les élèves, ne devrait pas poser
de problème. C'est lors du dénombrement du nombre de boutons
manquants que les difficultés vont apparaître.
Les différentes procédures
présentées ci-dessus (séance 1), pourront être
utilisées par les élèves. Le fait qu'ils soient
désormais en groupes va atténuer les erreurs possibles, puisque
les groupes seront formés de façon
hétérogènes et le dénombrement pourra être
discuté entre les élèves.
Lorsque les élèves se seront mis d'accord sur le
nombre de boutons manquants, le fait de demander au marchand peut poser
problème : certains élèves pourront avoir oublié le
nombre de boutons dénombrés entre temps, ou pourront ne pas
savoir exprimer le mot associé au nombre de boutons. J'aurai pour
rôle à ce moment là, de vérifier le nombre de
boutons manquants avant d'autoriser un élève à se lever
pour aller
demander au marchand, pour qu'il n'y ait pas de confusion
entre chaque groupe et que lors d'un oublie, je puisse l'aider.
Il sera aussi judicieux de s'intéresser à la
façon dont l'élève demande au marchand pour pouvoir se
faire une idée de la représentation du nombre qu'il a (exemple :
l'élève demandera 26 boutons ou l'élève demandera 2
plaques de dix boutons et 6 boutons isolés). A ce stade de
l'expérimentation, on peut imaginer que demander le nombre total de
boutons facilitera la compréhension de tous.
Je vérifierai également que les marchands
donnent le nombre exact de boutons demandés par l'élève,
puisque s'il est erroné, ce ne sera pas dû à une erreur de
dénombrement mais bien à une erreur de la part du marchand et
elles sont à éviter pour ne pas influer sur l'objectif de la
séance.
Les documents du Grand Ziglotron permettront de
vérifier de la réussite ou de l'échec du groupe :
- s'il y a le nombre de boutons exact collés sur le
Ziglotron et aucun bouton sur la table : les élèves auront
correctement dénombrés.
- S'il y a le nombre de boutons exact collés sur le
Ziglotron et qu'il reste des boutons sur la table : les élèves
n'auront pas correctement dénombrés.
- S'il n'y a pas le nombre suffisant de boutons collés
sur le Ziglotron : les élèves n'auront pas correctement
dénombrés.
Séance 3
La séance 3 reprend la même situation que la
séance 2 sauf que l'on y introduit des contraintes :
- écrire le nombre de boutons sur un bon de commande,
ainsi que le nombre de plaques et le nombre de boutons isolés
- les marchands ne peuvent pas donner plus de 9 boutons
isolés
- interdiction de parler aux marchands

'-' 43 '-'
Cette séance va amener à la compréhension
et à l'utilisation de la valeur positionnelle des chiffres dans
l'écriture d'un nombre.
Les procédures des élèves concernant le
dénombrement seront les mêmes que lors de la séance 1 et
2.
La contrainte de ne pas parler aux marchands va amener les
élèves à réfléchir sur ce qu'ils devront
écrire sur leurs bons de commandes. Comme lors de la séance 1,
certains élèves n'auront toujours pas les notions requises pour
indiquer avec précision le nombre de paquets de dix et de boutons
isolés par rapport au nombre total de boutons. C'est pour cela qu'une
aide leur sera permise : entourer des paquets de dix boutons pour pouvoir
compter le nombre de paquets qu'il faudra. Cette aide est indispensable pour
que les bons de commandes soient lisibles par les marchands et que les
écritures des nombres coïncident.
Malgré l'explication et l'aide apportée,
certains élèves pourront faire des erreurs entre les deux
écritures du nombre. C'est pour cela qu'il sera indiqué aux
marchands de s'intéresser uniquement au nombre de boutons total.
Le fait que les marchands ne puissent plus donner plus de neuf
boutons isolés va être une contrainte qui va poser beaucoup de
soucis aux élèves puisqu'ils ne sauront pas comment la contourner
s'ils n'ont pas les notions nécessaires. Les groupes les plus en
difficultés pourront être aidés, soit par leurs pairs, soit
par l'enseignante.
La réussite ou l'échec des groupes seront
jugés de la même façon que lors de la deuxième
séance.
Cette situation terminée et explicitée, on
propose aux élèves une autre activité permettant de
travailler sur l'oral des nombres. En effet, en leur demandant de
décomposer un nombre donné en paquets de dix et boutons
isolés, les élèves vont être amenés à
réfléchir sur la composition d'un nombre, sans avoir de
matériel à disposition. Les procédures utilisées
par les élèves lors de cette activité seront difficilement
observables, puisqu'il s'agit d'un calcul mental. Les élèves
pourront alors :
- compter avec leurs mains (combien de fois dix doigts il y a
dans ce nombre ?) et leurs doigts (combien de doigts en plus ?)
'-' 44 '-'
- connaître la réponse par rapport à
l'écoute du nombre (exemple : dix-neuf = un paquet de dix et neuf
doigts) mais cela ne marchera que pour les nombres de 10 à 19.
- Connaître la réponse grâce à leurs
connaissances
- Ecrire une réponse au hasard
Pour ne pas que les élèves puissent s'aider des
réponses de leurs camarades, il sera précisé que toutes
les ardoises devront être levées en même temps, lorsque
l'enseignante dit « Tic, tac, boum ».
Une explication des erreurs faites par les
élèves entre chaque nombre donné permettra une meilleure
compréhension au fur et à mesure de l'exercice.
Le vocabulaire des mots « dizaines » et «
unités » sera introduit et explicité en fin de
séance.
Séance 4
La séance 4 aura pour objectif de remplir le bon de
commande donné par l'enseignante afin d'y indiquer combien de paquets de
dix boutons et de boutons isolés il y a dans un nombre.
Cette situation reprend le même travail fait
précédemment sur l'ardoise à l'écrit. Les
élèves n'ont plus de matériel à leur disposition ;
c'est le moment où ils pourront institutionnaliser.
Les élèves reçoivent chacun un bon de
commande qu'ils doivent remplir individuellement. Sur ce bon est inscrit :
« Il faut 42 boutons. Notre commande : É paquets de dix boutons,
É boutons. ».
Cette activité assez courte va permettre de voir si les
élèves ont compris le sens du nombre. Une petite feuille blanche
leur sera donnée afin qu'ils puissent l'utiliser comme brouillon. C'est
grâce à cette feuille que l'on pourra relever les
procédures des élèves qui pourront être de :
- dessiner le nombre total de boutons puis d'entourer des paquets
de dix
'-' 45 '-'
- dessiner directement des paquets de dix
- d'écrire des décompositions du type :
10/10/10/10/2 ou alors 10/20/30/40/42 - décomposer le nombre sous forme
additive : 42 = 10+10+10+10+2
Les erreurs seront relevées directement sur le bon de
commande et pourront être dues à une mauvaise compréhension
du nombre ou à des chiffres écrits au hasard par exemple.
Une mauvaise compréhension de la consigne ne sera
probablement pas possible à ce stade de l'expérimentation,
puisqu'il s'agit d'une activité qu'ils ont déjà
travaillé au préalable.
L'activité de la séance 3 sur l'ardoise est
reprise lors de cette séance. En revanche, ce n'est plus un nombre de
paquets de dix boutons et de boutons isolés qui sont demandés
mais un nombre de dizaines et d'unités. Les procédures possibles
seront les mêmes que lors de la séance
précédente.
Séance 5
La séance 5 reprend la même évaluation que
lors de la première séance et permet de vérifier de la
validation ou non de l'hypothèse de recherche. En effet, c'est
grâce à la comparaison des deux évaluations que l'on pourra
observer l'évolution ou les lacunes persistantes des
élèves.
Les procédures des élèves seront les
mêmes que lors de la première séance. En revanche, on
s'attend à ce que les élèves forment des paquets de dix
pour dénombrer. Cela signifiera que le sens du nombre à
été compris grâce au groupements par dix.
Les erreurs attendues ne sont pas les mêmes que lors de
la première séance, puisque grâce à
l'expérimentation, les élèves devront avoir acquis
certaines connaissances leur permettant de répondre correctement
à cette évaluation.
Le choix de ne pas compliquer l'évaluation permettra de
faire une véritable comparaison entre le début et la fin de
l'expérimentation.
Ces cinq séances menées lors de
l'expérimentation vont permettre de relever
certaines erreurs et procédures des élèves
que l'on a explicitées ci-dessus. D'autres procédures ou erreurs
pourront apparaître sans avoir été analysées au
préalable.
C'est lors de l'analyse a posteriori que l'on pourra recueillir
les différentes façons d'exécution de la tâche par
les élèves et relever également leurs différentes
erreurs.
II. Analyse a posteriori
Séance 1
Lors de la première séance, dix-sept
élèves étaient présents. Une grille d'observation
pour relever les différentes procédures des élèves
a été utilisée. Il a été
précisé aux élèves de faire comme ils souhaitaient
pour dénombrer, y compris utiliser son crayon ; la procédure dite
« sans trace » est celle dans laquelle les élèves n'ont
laissé aucun trait de crayon ou aucune trace écrite :
|
Procédures de dénombrement
|
Nombre d'élèves
|
|
Barrer les billes / mettre un point
|
13
|
|
Faire des paquets
|
0
|
|
Dénombrer sans trace
|
3
|
|
Autres procédures
|
1
|
L'élève ayant utilisé une autre
procédure a écrit la comptine numérique dans chaque bille.
Sa procédure était incorrecte à chaque fois du fait qu'il
ait oublié une bille, ou que la comptine n'était pas correcte.
Lors de l'évaluation, dans le premier exercice de
dénombrement de billes (que
j'appellerai ci-dessous exercice 1), il y avait 28 billes au
total. Dans le deuxième dénombrement (exercice 2), il y en avait
22 et dans le troisième (exercice 3), 36.

'-' 47 '-'
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Dénombrement total de
billes
correct
|
9
|
10
|
4
|
|
Dénombrement total de
billes
incorrect
|
8
|
7
|
13
|
On remarque que les résultats corrects du
dénombrement de billes sont en corrélation avec le nombre de
billes à dénombrer ; plus les nombres sont grands, plus les
élèves ont des difficultés à dénombrer. A ce
niveau, les élèves devaient avoir connaissance de la comptine
numérique jusqu'à 100, mais certains devaient avoir des
lacunes.
C'est parmi tous les dénombrements corrects que nous
allons voir les procédures utilisées par les élèves
:
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Procédure : barrer/pointer
|
9/9
|
9 /10
|
4/4
|
|
Procédure sans trace
|
0/9
|
1/10
|
0/4
|
|
Autres procédures
|
0/9
|
0/10
|
0/4
|
On remarque clairement que les élèves ayant
dénombré correctement sont ceux ayant barrer ou pointer les
billes. On peut imaginer que la procédure la plus experte est bien de
les barrer ou de les pointer afin de laisser une trace qui rend compte des
éléments déjà dénombrés.
Sur les bonnes réponses, seulement trois
élèves ont correctement écrit le nombre de dizaines et
d'unités en fonction de leurs réponses trouvées ; en
effet, même si leurs dénombrements de billes au total
n'étaient pas corrects pour les trois exercices, ils correspondent quand
même à l'écriture du nombre sous la forme dizaines et
unités.
C'est à lors que l'on peut s'apercevoir que les
élèves de cette classe n'ont que très peu de connaissances
par rapport aux groupements décimaux.
Séance 2
Lors de la situation du Grand Ziglotron, dix-neuf
élèves étaient présents et dispersés en neuf
groupes. Cette séance était la présentation de la
situation et ne révèle pas vraiment d'éléments
indispensables à l'appropriation de l'apprentissage du nombre puisqu'il
s'agissait de dénombrer et de coller. Nous pouvons tout de même
nous intéresser aux élèves ayant réussi ou
échoué :
|
6 5 4 3 2 1 0
|
|
|
|
|
Nombre de groupes
|
|
Elèves qui avaient trop de boutons
Eleves qui n'avaient pas assez de boutons
|
Réussite Echec
Lors de cette séance, les procédures les plus
utilisées par les élèves ont été de
dénombrer terme à terme en recomptant plusieurs fois puisqu'ils
étaient par binômes. Les élèves qui ont
échoué n'ont pas tenu compte du fait qu'il fallait demander un
nombre de boutons exact : ni trop, ni pas assez. C'est pour cela que certains
ont redemandé des boutons (chose qui n'a pas été possible)
et d'autres en avaient trop.
Il est important de préciser que lors de cette
séance, les trois marchands désignés ont
réalisé l'activité quand tous les groupes avaient leurs
commandes et je jouais le rôle de la marchande.
Cette séance d'appropriation de l'activité a
été correcte dans le sens ou beaucoup d'erreurs vis-à-vis
des consignes ont été commises ; c'est à ce moment
là que les élèves ont pu se rendre compte des
différentes règles à respecter et qui serviront lors de la
séance suivante.

'-' 49 '-'
Séance 3
Cette séance sera analysée en deux parties :
tout d'abord la situation du Grand Ziglotron, puis l'exercice sur ardoise. Il
est également important de préciser qu'un rappel de la
séance précédente a été fait en début
de séance.
La situation du Grand Ziglotron :
Dans cette situation, nous ne nous intéresserons
évidemment pas au nombre de boutons dénombré par les
élèves (correct ou non), mais au lien qu'ils font entre les deux
écritures des nombres. En effet, ayant rempli le bon de commande
(à cause des contraintes), les élèves devaient donc donner
le nombre de boutons total, le nombre de paquets de dix boutons et le nombre de
boutons isolés.
Parmi les huit groupes d'élèves présents
ce-jour là, nous allons voir combien d'entre eux ont réussi ou
échoué lorsqu'ils ont du écrire le nombre de paquets de
dix et de boutons, si ces nombres ont un lien avec le nombre total de boutons,
mais aussi les procédures qu'ils ont utilisé.
Les nombres de boutons à dénombrer
étaient différents selon trois documents : 28, 34 ou 45
boutons.
Sur les huit groupes :
- Un groupe n'a rien écrit dans les catégories
« paquets de dix boutons » et « boutons ».
- Un groupe a écrit le même nombre pour chaque
catégories (41 boutons, 41 paquets de dix boutons, 41 boutons.).
Ces deux groupes ont probablement manqué de
connaissances par rapport aux paquets de dix boutons et de boutons seuls et se
sont retrouvés en difficultés lors de l'exercice. Les contraintes
ont également été un obstacle pour eux.
- Un groupe a utilisé les mêmes chiffres que
celui du nombre de boutons total mais dans le mauvais ordre : « Il y a 35
boutons. 5 paquets de dix boutons, 3 boutons. ». Les élèves
de ce groupe se sont sûrement rappelé du fait qu'il
s'agissait des mêmes chiffres mais n'ont pas
intégré le sens. Ces élèves n'ont pas
utilisé de stratégie de groupement.
- Deux groupes d'élèves ont groupé par
dix boutons sur leurs Ziglotrons mais n'ont pas su correctement
dénombrer par la suite (exemples : « Il y a 32 boutons, 3 paquets
de dix boutons, 3 boutons », « Il y a 28 boutons, 2 paquets de dix
boutons et 7 boutons ».). Ici, les élèves ont utilisé
une méthode intéressante qui est celle de grouper par dix mais
leurs résultats ne coïncident pas, puisque leurs
dénombrements de paquets de boutons et de boutons n'étaient pas
corrects. Ceci est probablement dû au fait qu'ils n'ont pas fait de lien
entre les deux écritures.
- Enfin, trois groupes d'élèves ont
entouré des paquets de dix sur leurs Ziglotrons et ont correctement
dénombré. En effet, ils ont noté le bon nombre de paquets
de dix boutons et le bon nombre de boutons sauf qu'ils ne sont pas en lien avec
le nombre de boutons total dénombré au départ (Exemple :
le nombre de boutons total à dénombrer est 37 ; sur le bon de
commande il sera écrit 39 boutons ; 3 paquets de dix boutons, 7
boutons). C'est en formant des groupements de dix que les élèves
ont su correctement donner les nombres de paquets de dix et de boutons.
Sur ces huit groupes, cinq groupes d'élèves ont
groupé par dix. Ceci a été amené au fur et à
mesure de la séance par un travail oral avec les élèves
dans lequel ils devaient trouver des stratégies efficaces pour
répondre à l'exercice. Des aides ont été
apportées au cours de la séance puisque les élèves
se sont retrouvés bloqués à cause de la contrainte du
marchand qui ne pouvait pas donner plus de 9 boutons isolés. Une mise en
commun a été faite en demandant aux élèves comment
ils pourraient compter les paquets de dix. Les élèves ont su dire
qu'il fallait faire des paquets de dix. Cela leur a permis de continuer
l'activité sans difficulté supplémentaire.
Dans cet exercice, les contraintes ont posé
énormément de problèmes pour les élèves. Le
fait de ne pas pouvoir demandé un nombre supérieur à 9
boutons isolés les a mis en difficulté dès le
départ. Sans une mise en commun sur la stratégie efficace du
groupement par dix, les élèves se seraient retrouvés
bloqués.
Exercice sur l'ardoise

Après avoir explicité les différentes
stratégies utilisées par les élèves lors de la
situation du Grand Ziglotron, nous avons commencé l'exercice sur
l'ardoise.
Six « calculs » ont été demandé
aux élèves :
- quatre pour le nombre de paquets de dix et de boutons
lorsqu'on leur donne un nombre de boutons total
- deux pour l'inverse
Il a été dit aux élèves que
paquets de dix s'écrivaient « P » sur l'ardoise et boutons
« B ».
Lors du premier calcul, certains élèves ont
formé des paquets de dix avec leurs dix doigts ; par exemple, lorsqu'il
était demandé « 34 », les élèves
tendaient trois fois leurs dix doigts et finissaient par montrer 4 avec une
main. Cette stratégie a été reprise en mise en commun
directe pour faciliter le travail des élèves. En revanche, on
comptait de dix en dix en même temps que l'on montrait nos dix doigts,
pour que les élèves l'intègrent aussi autrement par le
visuel.
La majorité des réponses des
élèves ont été bonnes durant tout l'exercice.
Seulement quelques élèves en difficultés écrivaient
des réponses erronées sur leurs ardoises (exemples : 34 = 4P 3B ;
34P ; 34 B).
L'exercice a bien fonctionné dans la mesure ou
seulement deux élèves avaient des difficultés qui se sont
estompées au fur et à mesure des mises en commun.
C'est à lors que les notions de « dizaines » et
« unités » ont été explicitées.
Séance 4
La séance 4 est une institutionnalisation du sens de la
numération grâce à la situation du Grand Ziglotron. En
effet, les élèves n'ayant qu'à remplir le bon de commande
se sont retrouvé directement face au sens de l'écriture sous
forme dizaine et unité d'un nombre.
Le nombre donné sur le bon de commande était de
42 boutons. Les élèves devaient donc compléter avec 4
plaques de dix boutons et 2 unités.

Sur 19 élèves, 18 ont répondu
correctement à cet exercice. Seul un élève a
répondu « 24 paquets de dix boutons, 14 boutons ».
Les élèves ont très rapidement su
répondre à l'exercice ; en sept minutes tous les
élèves avaient terminé.
Seul un élève s'est servi de la feuille de
brouillon pour y noter : « 10 20 30 40 42 ».
Ces résultats amènent à penser que les
élèves commencent à comprendre le sens de la
numération puisque, sans matériel, ils ont presque tous
répondu correctement. Nous pouvons aussi penser que c'est grâce
à la situation qui commence à être habituelle que les
élèves ont pu répondre correctement. A ce moment de
l'expérimentation, nous ne pouvons pas donner de conclusion.
L'exercice sur l'ardoise est alors repris avec les
élèves.
Ce jour-ci, nous avons fait 14 calculs. En effet, comme la
première situation a été très rapide, nous avons eu
le temps de faire sept nombres à transformer en écriture dizaines
et unités et sept nombres écrits sous forme « dizaine,
unité » à reconstituer.
Les élèves ne devaient plus écrire «
P » pour paquets de dix mais « d » pour dizaines et « u
» pour unités à la place de « B » pour boutons.
Les nombres ont été choisis de façon
à ce que le nombre des dizaines ne soit jamais le même que celui
des unités. Ce choix a été fait pour complexifier la
tâche et pour identifier où apparaitraient les différentes
erreurs des élèves.
|
20 18 16 14 12 10 8 6 4 2 0
|
|
|
|
|
Nombre d'élèves
|
|
FAUX BON
|
24 35 41 46 58 67 73
Voici un histogramme permettant de relever les réponses
des élèves au fur et à mesure des calculs. Les nombres
demandés sont en abscisse.
'-' 53 '-'
On remarque très nettement que la majorité des
élèves ont de bonnes réponses lorsqu'il s'agit de donner
le nombre de dizaines et d'unités. Les quelques mauvaises erreurs sont
faites par des élèves en difficulté ou sont des erreurs
d'inattention des chiffres (exemple : 24 = 24d 0u). Ces erreurs ne sont pas
analysées car on a pu remarqué qu'elles variaient avec les
élèves, c'est-à-dire que ce n'était pas toujours
les mêmes élèves qui faisaient des erreurs de sens, mais
différents élèves qui faisaient des erreurs de confusion.
Nous pouvons penser que les erreurs, plus nombreuses, lors du nombre 73, ont
été causées par le fait que 73 est un grand nombre dont la
sonorité se rapproche de 60 et de 13, ce qui a porté a confusion
chez les élèves.

3d 2u 4d 5u 5d 9u 5d 1u 6d 8u 8d 4u 9d 0u
20
18
16
14
Nombre d'élèves
12
FAUX
10
BON
8
6
4
2
0
Voici le graphique des calculs inverses :
On remarque que, demandés sous la forme dizaines et
unités, les calculs sont plus réussis par les
élèves. En effet, ils entendent et voient mentalement les
chiffres demandés de façon directe. Ils peuvent alors
reconstituer le nombre de façon plus simple que lors de calculs
inverses.
Les trois erreurs faites par les élèves lors du
nombre « 9d 0u » ont été dues au fait que les
élèves ne savaient pas comment écrire ce nombre. Le
zéro a porté a
'-' 54 '-'
confusion et il serait intéressant de réutiliser
les nombres « ronds » afin de palier aux difficultés.
Globalement, nous pouvons remarquer que cette séance
représente un tournant dans l'apprentissage de la numération par
les élèves puisque c'est à partir de là qu'ils
commencent à y mettre du sens grâce à des exercices
d'entraînement répétitif et un travail à l'oral
très présent.
Séance 5
La séance 5 reprend l'évaluation de la
première séance. C'est grâce à celle-ci que nous
allons pouvoir repérer les évolutions ou les lacunes persistantes
des élèves.
Il y avait 16 élèves présents.
Nous allons donc reprendre les mêmes données que
lors de la première séance :
|
Procédures de dénombrement
|
Nombre d'élèves
|
|
Barrer les billes / mettre un point
|
6
|
|
Faire des paquets
|
10
|
|
Dénombrer sans trace
|
0
|
|
Autres procédures
|
0
|
On remarque que la majorité des élèves
ont utilisé le groupement. En effet, les groupements comportent dix
billes à chaque fois. Les élèves ont alors
institutionnalisé le fait que pour dénombrer plus facilement et
de manière plus stratégique, il était intéressant
de créer des groupements de dix.
Reprenons désormais le tableau permettant de
vérifier l'échec ou la réussite des élèves
selon les trois exercices :
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Dénombrement total de
billes
correct
|
8
|
13
|
9
|
'-' 55 '-'
|
Dénombrement total de
|
|
|
|
|
8
|
3
|
7
|
|
billes incorrect
|
|
|
|
Grâce à ces résultats, nous pouvons voir
qu'une majorité des élèves ont répondu correctement
lors du dénombrement de billes total pour les exercices 2 et 3 et que la
moitié de ceux-ci ont répondu correctement pour le premier
exercice. Ceci démontre que grâce aux groupements, les
élèves ont éprouvé moins de difficultés
à dénombrer et que, même s'ils n'ont pas groupé, ils
obtiennent des résultats corrects dans la plupart des cas. Ceci est peut
être également dû au fait que les exercices ont
été refaits à plusieurs reprises et que les
élèves n'avaient pas la contrainte de la compréhension
pour réussir.
Nous allons maintenant voir quelles procédures ont
été les plus expertes dans la résolution de ces exercices,
parmi les résultats corrects :
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Procédure :
barrer/pointer
|
4/8
|
5/13
|
5/9
|
|
Faire des
groupements de dix
|
4/8
|
8/13
|
4/9
|
Les résultats restent très mitigés ; il
est vrai qu'entre les élèves ayant barrer ou pointer et les
élèves ayant dénombré, il n'y a pas de
différences notables (sauf pour l'exercice 2 où la
procédure de groupement est privilégiée).
Intéressons-nous maintenant à la partie la plus
intéressante qui est de savoir si les élèves ont
correctement donné l'écriture du nombre sous la forme de dizaines
et d'unités. Nous relèverons les écritures correctes pour
les dénombrements de billes au total qui sont bons, mais
également, pour ceux qui sont faux, puisqu'ils peuvent coïncider
(exemple : si l'élève a dénombrer un nombre faux de billes
au total mais que l'écriture du nombre sous la forme dizaines et
unités est en adéquation avec le nombre de départ, le
résultat est considéré comme bon).
|
Exercice 1
|
Exercice 2
|
Exercice 3
|
|
Ecriture des
dizaines et
unités
correcte
|
10
|
11
|
8
|
|
Ecriture des
dizaines et
unités
incorrecte
|
6
|
5
|
8
|
Il est indispensable de rappeler que lors de la
première évaluation, seuls trois élèves avaient
donné des écritures correctes au moment de donner les dizaines et
les unités.
Lors de cette évaluation, même si les
élèves n'ont pas tous correctement dénombrer les billes,
ils ont quand même, pour la majorité des cas, trouvé des
réponses justes en ce qui concerne l'écriture sous la forme
dizaines et unités. Ils ont fait le lien entre les deux écritures
et ont nettement progressé par rapport aux connaissances de
départ.
III. Interprétation
Cette expérimentation a été mise en place
dans le but d'aider les élèves à donner du sens à
la numération, et plus particulièrement au système
décimal de numération français. En effet, lors des
apprentissages premiers au cours préparatoire, les élèves
sont amenés à décomposer les nombres sans pour autant en
comprendre leur sens. Par conséquent, ils amassent des
difficultés cognitives qui les suivront jusqu'à la fin de leur
scolarité.
Pour répondre à ma problématique qui
était de savoir si créer une situation articulant l'oral et
l'écrit et mettant en place l'élaboration du groupement par 10,
permettait une meilleure compréhension de notre système
français de numération décimale, j'ai
réalisé une expérimentation sur cinq séances.
Lors de cette expérimentation, des situations ont
été mises en place afin d'amener les élèves
à travailler selon différentes modalités :
individuellement, en collectif, en

'-' 57 '-'
groupes, sur ardoise, grâce au Grand Ziglotron etc.
É Lors de ces différentes situations, les élèves
ont pu intégrer la numération de façon approfondie, en y
donnant du sens et en construisant un savoir de façon progressive. En
travaillant petit à petit et en offrant aux élèves la
possibilité de s'entraîner sur le thème essentiel qu'est la
numération, nous avons pu développer chez eux des connaissances
qu'ils n'avaient pas.
Apprendre la numération et en connaître son sens
est une étape très importante dans la scolarité d'un
élève. Il est donc important de mettre en place
différentes séquences leur permettant de travailler de
manière approfondie sur un thème ciblé.
Après avoir mené l'expérimentation
ci-dessus, je peux admettre que les élèves ont de meilleures
connaissances qu'au départ vis-à-vis de la numération
décimale. En effet, on peut nettement remarquer que les résultats
de l'évaluation de départ et ceux de l'évaluation finale
sont très évolutifs.
Voici un tableau récapitulatif des résultats des
élèves lors de l'évaluation diagnostique et lors de
l'évaluation finale :
|
Evaluation initiale
|
Evaluation finale
|
|
Dénombrement
total de billes
|
Ecriture : paquets
de dix, boutons
|
Dénombrement
total de billes
|
Ecriture : paquets
de dix, boutons
|
|
Alice
|
Faux
|
Fausse
|
Faux
|
Fausse
|
|
MIna
|
Correct
|
Correcte
|
Correct
|
Correcte
|
|
Yanni
|
Faux
|
Fausse (mais
concordant avec
le
dénombrement
total)
|
Correct
|
Correcte
|
|
Daniela
|
Correct
|
Correcte
|
Correct
|
Correcte
|
|
Tracy
|
Faux
|
Fausse
|
Absente
|
Absente
|
|
Nadim
|
Correct
|
Rien
|
Correct
|
Correcte
|
|
Ayoub
|
Correct
|
Rien
|
Faux
|
Fausse (mais
concordant avec
|
|
|
|
|
le dénombrement
total)
|
|
Lorenzo
|
Correct
|
Rien
|
Correct
|
Correcte
|
|
Keily
|
Correct
|
Rien
|
Faux
|
Fausse
|
|
Kaïs
|
Correct
|
Rien
|
Faux
|
Fausse
|
|
Fara
|
Faux
|
Rien
|
Faux
|
Fausse
|
|
Yasmine
|
Correct
|
Fausse
|
Faux
|
Fausse (mais
concordant avec
le
dénombrement
total)
|
|
Nohémie
|
Faux
|
Fausse
|
Correct
|
Correcte
|
|
Andréa
|
Correct
|
Rien
|
Faux
|
Fausse
|
|
Yassine
|
Faux
|
Fausse
|
Correct
|
Correcte
|
|
Aboubacar
|
Faux
|
Rien
|
Correct
|
Faux
|
|
Zakaria
|
Faux
|
Rien
|
Faux
|
Fausse (mais
concordant avec
le
dénombrement
total)
|
Ce tableau est indicatif des résultats de l'exercice 1
de l'évaluation, car c'est celui qui donne, selon moi, le maximum
d'informations. Effectivement, les élèves sont sûrement
plus concentrés lors du premier exercice et c'est celui où le
nombre total est de 28, donc aucune difficulté numérique pour les
élèves (par rapport à l'exercice 3 où le nombre de
billes était 36) et pas de confusion possible entre les paquets de dix
boutons et les boutons isolés (par rapport à l'exercice 3
où le nombre de billes était 22).
Sur les 16 élèves présents lors des deux
évaluations, nous avons mis en caractère gras ceux ayant
évolué par rapport à la première évaluation,
sur le résultat de l'écriture « paquets de dix boutons,
boutons » (dizaines, unités). En effet, presque tous les
élèves

'-' 59 '-'
ont évolué, dans le sens où s'ils
n'écrivaient aucune réponse lors de la première
évaluation, aucun d'entre eux n'a laissé de champ vide lors de la
deuxième. En revanche, et par rapport à l'intérêt de
mon expérimentation, les élèves qui ont
évolué par rapport au sens de la numération sont ceux qui
ont :
- donné un résultat correct pour
l'écriture « paquets de dix boutons, boutons »
- donné un résultat faux pour l'écriture
« paquet de dix boutons, boutons », mais concordant avec le
dénombrement total. Par exemple, s'ils ont dénombré au
total 29 billes (au lieu de 28) et qu'ils ont écrit « 2 paquets de
dix boutons et 9 boutons », leurs résultats sont
considérés comme évolutifs par rapport au savoir mis en
jeu.
La moitié des élèves ont
évolué par rapport au sens de la numération et à
l'écriture d'ordre donné (dizaines et unités). Ces
résultats ne sont absolument pas négligeables et indiquent que
l'expérimentation a été effective.
Pour que la totalité des élèves
connaissent une évolution, nous aurions pu allonger notre
expérimentation, ou encore mettre en place une évaluation
où le nombre de billes total serait déjà
dénombré, pour ne s'intéresser qu'au sens du nombre
travaillé lors de la séquence mise en place.
Les différents exercices mis en place ont permis aux
élèves de comprendre ce qu'était réellement les
dizaines et les unités (à ce niveau scolaire), et d'y attribuer
une définition précise. En travaillant sur une situation
présentant un certain matériel, tout en associant l'écrit
et l'oral, nous avons offert la possibilité aux élèves
d'élargir leurs champs cognitifs dans le domaine de la numération
décimale. Cette évolution peut également se
caractériser par le fait que les exercices ont été
répétés et retravaillés en classe. Les exercices
oraux sur l'ardoise ont également permis de faire avancer les
élèves au niveau des compétences qu'ils devaient
acquérir. Travailler sur des situations mettant en oeuvre le groupement
par dix est un excellent moyen de travailler profondément sur la
numération décimale.
Mon hypothèse de départ était d'admettre
qu'utiliser l'oral en simultanée de l'écrit à travers une
situation privilégiant le groupement par dix. Cette hypothèse est
alors vérifier grâce aux différents résultats des
élèves.
~ 60 ~
Conclusion
La numération est un apprentissage fondamental que
l'école doit pouvoir donner de la façon la plus claire possible
aux élèves. Pour cela, ils peuvent utiliser la mise en place
d'apprentissages intermédiaires permettant un apprentissage notion par
notion, pour une compréhension totale des élèves. La
notion de groupement est une notion intermédiaire utilisée dans
le domaine de la numération qui établit un lien avec l'aspect
décimal de notre système de numération.
Après confrontation des différents articles que
j'ai pu lire, j'ai pu comprendre que pour un apprentissage censé de la
numération, il fallait confronter plusieurs moyens d'apprentissage que
les différents auteurs ventent à travers leurs écrits. En
effet, cumuler l'écriture, l'oral, la manipulation, la résolution
autonome de problèmes par l'élève, tout en reliant tout
cela avec le sens de l'activité offre la possibilité à
l'élève de comprendre notre numération française de
façon poussée.
Ce mémoire me permet d'accéder à la
problématisation du thème important qu'est la numération
à travers la question : L'articulation de l'oral et de
l'écrit dans une méthode mettant en place l'élaboration du
groupement par 10, permettrait-elle une meilleure compréhension de notre
système français de numération décimale
?
L'hypothèse de recherche est aujourd'hui
validée. En effet, lors de l'expérimentation, nous avons
utilisé les différentes modalités présentes dans la
problématique et nous avons pu constater que les résultats
évoluaient considérablement.
Il est important de rappeler que cette recherche a
été faite sur un nombre de séances limitées (ici,
cinq), et que des recherches ultérieures peuvent être
menées. Nous pourrions, par exemple, observer les différents
élèves suivis à la fin de leur année de CP
et ainsi voir si les notions et savoirs travaillés sont
acquis. Aussi, nous pourrions poursuivre cela jusqu'au CE1.
Cette recherche a été faite sur une classe de 21
élèves de CP. Il est évident que les résultats
restent moindres et qu'une étude plus poussée pourrait se faire
sur un échantillon beaucoup plus important, afin de juger de sa
légitimité.

~ 62 ~
Bibliographie
Articles
AIGOIN, C. et GUEBOURG, V. (2004). Du dénombrement
terme à terme aux groupements réguliers : un pas
nécessaire vers la compréhension de notre système de
numération positionnelle !, Grand N, n° 73, pp. 49-65.
BEDNARZ, N. et JANVIER, B. (1984). La numération
(première partie). Les difficultés suscitées par son
apprentissage. Grand N, n°33, pp. 5-31.
HILLI, H. et RUELLAN-LE-COAT, J. (2009). « Freddy la
grenouille » ou la notion de groupement en CP. Grand N,
n°83, pp. 97-116.
Références internet
CHOLLET Jean. Les 5 principes de Gelman. 1 novembre 2009 [18 mars
2013].
http://circo89-joigny.ac-dijon.fr/IMG/pdf/documents_theoriques_d_appui.pdf
Programmes et bulletins officiels
MINISTERE DE L'EDUCATION NATIONALE ET MINISTERE DE L'ENSEIGNEMENT
SUPERIEUR ET DE LA RECHERCHE. (2008). Bulletin officiel, hors série
n°3 du 19 juin 2008.
MINISTERE DE L'EDUCATION NATIONALE ET MINISTERE DE L'ENSEIGNEMENT
SUPERIEUR ET DE LA RECHERCHE. (2012). Bulletin officiel n°1 du 5
janvier 2012.
Manuels scolaires
CHARNAY R. (sous la direction de) (2009). Cap maths CP.
Paris. Hatier.


~ 64 ~
Annexes
Annexe 1 : Fiche document du Grand Ziglotron
Annexe 2 : Bons de commande (séances 3 et 4)



Annexe 3 : Production d'élève Ð
Evaluation initiale - procédure pointage des éléments
(séance 1)
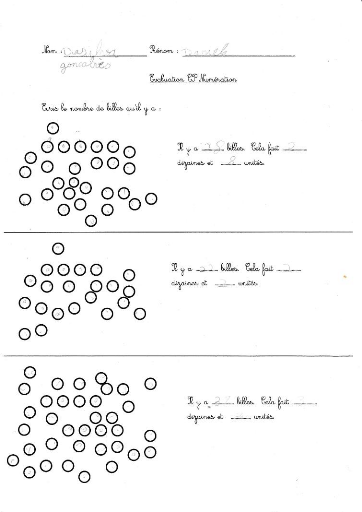

Annexe 4 : Production d'élève Ð
Evaluation initiale - procédure sans trace (séance 1)


Annexe 5 : Production d'élève Ð
Evaluation initiale - procédure comptine numérique (séance
1)


Annexe 6 : Production d'élèves - Pas
assez de boutons (séance 2)


Annexe 7 : Production d'élèves - Nombre
exact de boutons (séance 2)


Annexe 8 : Production d'élèves -
Ziglotron + bon de commande associé (séance 3)


Annexe 9 : Production d'élèves :
Ziglotron + bon de commande associé (séance 3)


'-' 73 '-'
Annexe 10 : Production d'élèves :
Ecriture correcte (séance 4)

'-' 74 '-'
Annexe 11 : Production d'élève - Ecriure
incorrecte (séance 4)

Annexe 12 : Production d'élèves - Deux
brouillons bons de commande (séance 4)


'-' 75 '-'
Annexe 13 : Production d'élève -
Evaluation finale - procédure de groupement par dix + pointage des
elements (séance 5)

| 


