III.3.AUTRES TESTS ECONOMETRIQUES
1° test d'autocorrélation des erreurs
Les hypothèses H3 et H4 stipulent successivement que
les erreurs sont non corrélées (ou indépendantes) et que
la variance des erreurs est constante (homoscédasticité). Lorsque
H3 est violée, nous sommes donc en présence
d'autocorrélation des erreurs. Les estimateurs restent sans biais mais
ne sont plus à variance minimale. Dans l'état normal des choses,
la matrice des variances covariances des erreurs est :
251654144251653120
E (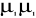 ) E ( ) E (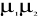 ) ... E ( ) ... E (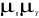 ) ) 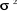 0 ... 0 0 ... 0
E (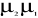 ) E ( ) E (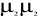 ) ... E ( ) ... E (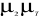 ) 0 ) 0 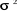 ... 0 ... 0
Ùì=E (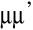 ) = ... = ...
= ) = ... = ...
= 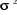 I I
E ( ) E ( ) E ( ) ... E ( ) ... E (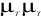 ) 0 0 ... ) 0 0 ...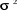
En cas d'autocorrélation des erreurs, cette matrice
n'est plus composée de zéro à l'extérieur de la
diagonale principale, puisque dans ce cas, Cov(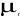 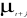 ) ? 0, pour j ? 0. ) ? 0, pour j ? 0.
Ùì ? 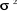 I lorsque il y a autocorrélation car plusieurs termes
non diagonaux et éventuellement tous deviennent non nuls. H3 n'est plus
vérifiée car Cov( I lorsque il y a autocorrélation car plusieurs termes
non diagonaux et éventuellement tous deviennent non nuls. H3 n'est plus
vérifiée car Cov(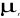 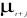 ) ? 0. ) ? 0.
1 2 3 4 5 6 7 8 Temps
e4 e5
e6
e3 e7
e1 e2
e8
et +
0
-
251660288L'autocorrélation apparaît lorsque les
erreurs sont liées par un processus de reproduction. On distingue
l'autocorrélation positive de l'autocorrélation négative.
Autocorrélation positive
1 2 3 4 5 6 7 8 Temps
e3
e6
e2
e1 e3
e5 e7
et +
0
-
251661312
Autocorrélation négative
Plusieurs raisons peuvent justifier l'autocorrélation des
erreurs :
· l'absence d'une variable explicative importante dont
l'explication résiduelle permettrait de rendre « un bruit
blanc » les erreurs ;
· une mauvaise spécification du
modèle : la relation entre la variable dépendante et la(les)
variable(s) indépendante(s) est non-linéaire ;
· un lissage par moyenne mobile (MA) ou une interpolation
des données crée une autocorrélation artificielle des
erreurs due à l'usage de ces opérateurs c'est-à-dire une
erreur de mesure de la variable dépendante.
L'autocorrélation des erreurs est
fréquente dans le modèle en séries temporelles et peu
probable dans les modèles en coupes instantanés (cross-section
data) parce que la collecte des données s'effectue de manière
aléatoire et la succession des valeurs de la variable à expliquer
n'a aucune raison de générer une autocorrélation.
III.3.1. Les
conséquences de l'autocorrélation :
Les estimateurs de l'OLS demeurent sans biais car b =
(X'X)-1X'Y ne contient pas de variance de l'erreur, mais deviennent
inefficaces. En effet, var (b) ? ó2(X'X)-1. Or,
c'est la ó2b et ó b [ou SE(b)]
qui sont utilisées pour construire les tests d'hypothèses. Tous
les tests d'hypothèses deviennent faux c'est-à-dire que les
procédures d'inférence statistique ne sont plus valables.
La matrice Ùì = E(ì'ì)
? ó2I n'est plus composée de zéros
à l'extérieur de la diagonale principale puisque cov
(ìiìj) ? 0 et donc les estimateurs OLS
n'ont plus une variance minimale. En effet, ó2b =
E[(b-â) (b- â)'] = E{[(X'X)-1X'ì]
[(X'X)-1X'ì]'}
= E[(X'X)-1X'ìì' X
(X'X)-1] =
(X'X)-1X'E(ìì')X(X'X)-1 =
(X'X)-1X' Ùì X(X'X)-1
Ce qui veut dire que b estun estimateur de â dont la
première diagonale de la matrice des variances-covariances est
supérieure à celle de ó2(X'X)-1.
| 


