Phénomènes induits par le bruit dans les systèmes dynamiques décrits par des équations différentielles.

Chapitre 3

Étude qualitative des systèmes de

FitzHugh-Nagumo

Nous ajoutons maintenant les termes de bruit à l'équation (2.6) dans le cas où b =6 0. Nous considérons le système d'équations différentielles stochastiques :

? ?? ??

' 1 x= (x - x^3+ y)dt + o1dw1 t E ' y= (a - bx - cy)dt + o2dw2 t .

(3.1)

où o1 et o2 sont deux réels positifs représentant l'intensité du bruit, W ⁽¹⁾

t et W ⁽²⁾

t

sont deux mouvements browniens standards indépendants. D'après les théorèmes généraux [68], ce système admet une unique solution forte (xt, yt)t?[0,T] presque sûrement continue.

3.1 Limite inférieure du régime bruit fort

Nous cherchons à déterminer pour quels paramètres nous avons les trois comportements mis en évidence dans les simulations numériques. Nous nous plaçons dans le cas où le point d'équilibre est un foyer, c'est à dire pour ä = vå. Pour cela, nous transformons l'équation de FitzHugh-Nagumo en coordonnées polaires (r; è) introduites dans la proposition(2.4.4) après avoir transformé le système en coordonnées (î, æ) introduites dans la preuve de cette Proposition. En étudiant l'ordre de grandeur

3.1 Limite inférieure du régime bruit fort 69

des termes, nous obtenons un premier bruit de coupure ó_c. Il correspond à la limite

v

inférieure du bruit fort et est donné par ó_c = åä.

En faisant les mêmes transformations que pour la partie linéaire dans le cas déterministe, nous obtenons pour l'équation de FitzHugh-Nagumo (3.1) le résultat suivant :

Proposition 3.3.1. En coordonnées (r,è), pour 0 = ä = -vå, l'équation de FitzHugh-Nagumo (3.1) prend la forme

_r2 1

drt = [-uRrt 3a

åuI

t sinèt( Ä)² + 1 ( ó2

r3 t sinèt( Ä)³ + 1 cos²èt + ó² ₂sin²èt)]dt

åëI 2rt åë2 I

ó1

+ t
våëIsinètdW ⁽¹⁾

t + ó2cosètdW ⁽²⁾

3a

dèt = [ëI - rtcosèt(

åëI

Ä)² + 1

t cosèt( Ä)³]dt + ¹ [ ó1

r2 t

åëI rt våëI ]cosètdW⁽¹⁾ - ó2sinètdW ⁽²⁾

(3.2)

où

Ä = -uRî - uIæ

et nous rappelons la définition de uR et uI

uR = ä

å

vå - ä2

et uI =

å

Preuve. En translatant l'origine au point d'équilibre du système (x*,y*), le système de FitzHugh-Nagumo (3.1) s'écrit :

ådut = [(1 - 3a²)ut + vt - 3au²_t - u³_t]dt + våó1dW ⁽¹⁾

t

dvt = -utdt + ó2dW ⁽²⁾

t

Faisons ensuite le changement de variables qui permet d'obtenir la forme de Jordan pour la partie linéaire

uv 1R 0 æ

3.1 Limite inférieure du régime bruit fort 70

nous obtenons alors le système :

dît = = [-uRît - uIæt]dt + ó2dW ⁽²⁾

t

3a (Ät)² + ¹ (Ät)³]dt + ó1

dæt = [uIît - uRæt - dW⁽¹⁾

åuI åuI y/åuI

où

Ät = -uRît - uIæt

Passons ensuite en coordonnées polaires en posant

î = r cosè
æ = r sinè

Nous cherchons un système sous la forme

drt = ñ1(rt, èt)dt + ø¹₁(rt, èt)dW ⁽¹⁾

t + ø²₁(rt, èt)dW ⁽²⁾

^t (3.3)

dèt = ñ2(rt, èt)dt + ø¹₂(rt, èt)dW ⁽¹⁾

t + ø²₂(rt, èt)dW ⁽²⁾

t

D'après la formule d'Itô, nous avons

dît = cosètdrt - rtsinètdèt - ₂rtcosèt(dèt)²

1

(3.4)

1

dæt = sinètdrt + rtcosètdèt - ₂rtsinèt(dèt)²

où

(dèt)² = (ø²₁(rt, èt)dW ⁽¹⁾

t + ø²₂(rt, èt)dW ⁽²⁾

t )2

= [ø¹₂(rt, èt)² + ø²₂(rt, èt)²]dt

Par combinaison linéaire, nous obtenons :

drt = cosètdîtsinètdæt + 2rt[ø^1 1 2(rt, èt)^2 + ø^22(rt, èt)^2]dt rtdèt = -sinètdît + cosètdæt

(3.5)

3.2 Étude qualitative du rayon moyen du petit cycle 71

En remplaçant dît et dæt par les expressions du système (3.4) , nous avons :

_r2 1

drt = [-uRrt

åuI

3a

t sinèt( Ä)² + 1 ( ó2

r3 t sinèt( Ä)³ + 1 cos²èt + ó² ₂sin²èt)]dt

åëI 2rt åë2 I

ó1 + t våëI sinètdW ^(1) t + ó2cosètdW ^(2) 3a rtcosèt( Ä)^2 + 1 dèt = [ëI - r2 t cosèt åëI åëI où nous avons posé						( Ä)^3]dt + ^1 [ ó1 t rt våëI ]cosètdW^(1) - ó2sinètdW ^(2) (3.6)
1 uI	3a åuI	rcosè(	Ä)^2 ' 1 r( åu2 I	Ä)^2

Ä = -uRcosè - uIsinè

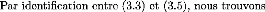
t

(rt,

t)

è

è

=ó1

cos våëIrt

ø2 2(rt, èt) = -ó2sinèt

rt

Nous n'avons plus qu'à remplacer ø¹₂(rt, èt) et ø²₂(rt, èt) dans l'équation (3.4), pour obtenir (3.2).