Phénomènes induits par le bruit dans les systèmes dynamiques décrits par des équations différentielles.

Chapitre 4

Simulation avec R

R est un logiciel de calcul scientifique R est un environnement intégré de manipulation de données, de calcul et

de préparation de graphiques. Toutefois, ce n'est pas seulement un " autre " environnement statistique (comme SPSS ou SAS, par exemple), mais aussi un langage de programmation complet et autonome.

4.1 Le modèle de Hull-White,Vasicek

Exemple d'application (dans chapitre 1)

L'intérêt pratique de la simulation d'équations diférentielles stochastiques est très important, car la résolution analytique n'est pas toujours facile. Cela rend difcile l'étude de l'évolution dynamique d'un phénomène, ou par exemple l'analyse statistique de la variable aléatoire : instant de premier passage (IPP) correspondant à la solution de l'équation, qui sera illustré dans ce chapitre. Aujourd'hui, le développement de l'outil informatique motive les scientifiques pour mettre au point des schémas numériques pour la résolution approchée des EDS.

Nous utilisons dans le paragraphe qui suit le Logiciel R avec le package Sim :DiffProc avec un sous programme personnel. Nous utilisons également le package Sim :Diff-ProcGui établi par Guidoum pour avoir d'autre aspects de la simulation.

Considérons le processus X à valeurs dans R solution de

dXt = r(è - Xt)dt + ódWt

4.1 Le modèle de Hull-White,Vasicek 86

ou r, è, u sont des constantes, W est un Ft-mouvement brownien. En posant

Zt = xt - è

par La formule d'Itô nous avons

dZt = dxt

= r(è - Xt)dt + udWt = -rZtdt + udWt

Le processus Z est un processus d'Ornstein-Uhlenbeck la solution sous forme intégrale est donnée par

Z t

Zt = z0e_^rt + ue_^rt e^rsdW_s

0

En remplaçant Zt par Xt - è nous obtenons

Z t

Xt - è = (X0 - è)e_^rt + ue_^rt e^rsdW_s

0

Z t

Xt = X0exp^(_rt) + è(1 - exp^(_rt)) + uexp(-rt) esp^(rt)dw_s

0

Simulation numérique des trajectoires

Nous simulons d'abord quelques trajectoires à l'aide du package Sim.DiffProcGui

Efectuons un changement de paramètres, par exemple, on prend u plus petite que 1,

pour voir l'efet du coefficient de diffusion sur la perturbation de la trajectoire

Nous remarquons que les trajectoires [4.3], [4.2] sont plus lisses que la trajectoire [4.1]

lorsque u est plus petite que 1

Nous pouvons aussi utiliser une autre méthode de simulation. La fonction "snssde"

permet de simuler numériquement la solution approchée des EDS. R> help("snssde")

R> example("snssde")

R> snssde(N, M, T = 1, t0, x0, Dt, drift, diffusion)

Détails :

N : La taille du processus.

M : Le nombre de trajectoires à simuler.

T : L'instant final.

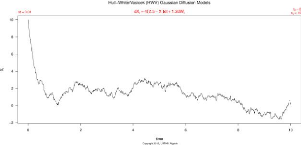
4.1 Le modèle de Hull-White,Vasicek 87

FIGURE 4.1 - Trajectoire du modèle de HWV avec è = 2.5, r = 4, u = 1.2

t0 : L'instant initial. x0 : La valeur initiale.

Dt : La discrétisation ou le pas (par défaut T = t0 + Dt * N)

Driff : Coefficient de dérive.

Diffusion : Coefficient de diffusion

Utilisons cette méthode pour le modèle de HWV

R> f<-expression(4 * (2.5 - x))

R> g<-expression(1.2)

R> res<-snnssde1d(driff=f,diffusion=g,M=1,x0=10,t0=0,T=10,N=1000,Dt=0.01)

R> plot(res,main="Le modèle de Hull-white/Vasicek",xlab="temps",ylab="Xt", sub="Xt=4(2.5-

Xt)+1.2dWt")

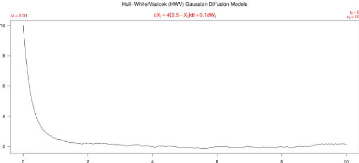
4.1 Le modèle de Hull-White,Vasicek 88

FIGURE 4.2 - Trajectoire du modèle de HWV avec è = 2.5, r = 4, ó = 0.1

Ornstein-Uhlenbeck simulation

xo = 10 mu = 2.5 sig = 1.2

alpha = 4

mesh = 100

t = 10

par(mfrow = c(1, 2),mar = c(2, 1.75, 1.5, 1),tck = -.03,mgp = c(3, .5, 0),cex.axis =

0.7)

bm = c(0, cumsum(rnorm(1000)))/sqrt(100)

xlist = numeric(1001)

for (iin0 : 1000)

xlist[i + 1] = xo * exp(-alpha * i/100) + mu * (1 - exp(-alpha * i/100)) +

sig * exp(-alpha * i/100)) * sum(exp(alpha * i/100) * (bm[1 : (i + 1)] - bm[1 : (i)]))

plot(seq(0, 10, .01),xlist,type = »l»,ylim = c(-2, 10),xlab = »»,ylab = »»)abline(h = -1,lty = 2)

for (iin1 : 1)

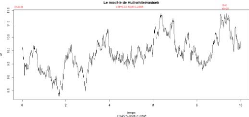
4.1 Le modèle de Hull-White,Vasicek 89

FIGURE 4.3 - Trajectoire du modèle de HWV avec è = 2.5, r = 4, ó = 0.01

bm = c(0, cumsum(rnorm(1000)))/sqrt(100)

xlist = numeric(1001)

for (iin0 : 1000)

xlist[i + 1] = xo * exp(-alpha * i/100) + mu * (1 - exp(-alpha * i/100)) +

sig * exp(-alpha * i/100) * sum(exp(alpha * i/100) * (bm[1 : (i + 1)] - bm[1 : (i)]))

lines(seq(0, 10, .01),xlist,type = »l»)

Interprétation

Pour un w fixé de manière aléatoire la simulation nous permet de mettre en évidence l'idée que la trajectoire de Xt(w) est de plus en plus lisse "presque dérivable" quand ó est proche de 0 (réduction de la perturbation), de plus si on prend ó nul l'équation différentielle stochastique devient une équation différentielle ordinaire dont la trajectoire de sa solution est complètement lisse "dérivable".

Remarque

En peut simules le tempe de premier passage avec la commande suivants "fptsde1d"

Exemple

dX(t) = -4 * X(t) * dt + 0.5 * dW(t)

S(t) = 0 (constant boundary)

set.seed(1234)

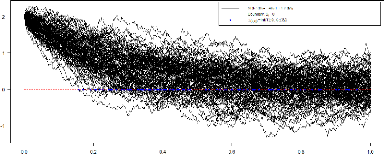
4.1 Le modèle de Hull-White,Vasicek 90

Method:

FIGURE 4.4 - Trajectoire du modèle de HWV avec = 2.5, r = 4, u = 1.2

FIGURE 4.5 - Trajectoire du modèle de HWV avec = 0.05, r = 0.01, u = 0.01

f<-expression( -4*x)

g<-expression(1.2)

St <- expression(0)

res1 <- fptsde1d(drift=f,diffusion=g,boundary=St,x0=2)

res1

plot(res1)

Les détailles de l'excusions

Ito Sde 1D :

dX(t) = -4 * X(t) * dt + 1.2 * dW(t)

4.1 Le modèle de Hull-White,Vasicek 91

Euler scheme of order 0.5

Summary :

Size of process N = 1000.

Number of simulation M = 100.
Initial value x0 = 2.

Time of process t in [0,1].

Discretization Dt = 0.001.

boundary [1] 0

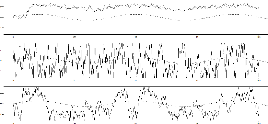
Exemple de resonoce stochastique

La résonance stochastique est un phénomène par lequel la transmission d'un signal utile ou cohérent, par certains systèmes non linéaires, peut être améliorée par l'aug-mentation du bruit appliqué au système.

dx dt

+ ît

= [x - x³ + s(t)]¹

~

ó

avec s(t) = Asin(2ðv0t) et ît = _v~dWt

simulation(R)

par(mfrow=c(1,3),mar=c(2,1.75,1.5,1),tck=-0.03,mgp=c(3,.5,0))

sig <- c(0.2,2,0.8) set.seed(20) for (k in 1 :3) sigma<- sig[k]

T <- 100 n <- 600 A <- .3 z <- 1

w <- 2*pi/40

x <- numeric(n+1)

x[1]<- 0

for (i in 2 :(n+1)) x[i] <- x[i-1] + (z*x[i-1] - z*x[i-1]³ + A * sin(w * T * (i - 1)/n)) *

T/n + sigma * sqrt(T/n) * rnorm(1)

plot(seq(0,T,T/n),x,type = »l»,ylim = c(-1.5, 1.5),xaxt = »n»,xlab = »»,ylab =

»»,yaxt = »n», lwd = 0.5)

axis(2, c(-1, 0, 1))

axis(1, c(0, 25, 50, 75, 100))

curve(A * sin(w * x), 0, 400, lty = 2, add = TRUE)