Etude prévisionnelle de la consommation nationale du gaz en Algérie

5.2 Etude de la Serie de consommation des centrales electriques (CE)

5.2.1 IdentiÖcation

La série O Et représente líévolution mensuelle de la consommation nationale du gaz na- turel des centrales électriques sur une période allant de janvier 1997 a décembre 20 0 4.

^{a-Representation graphique de la serie brute O E}t

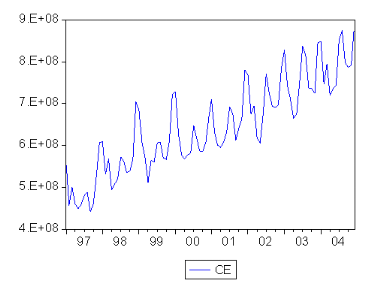
^{FIG.II.1ó Graphe de la serie brute O E}t

La représentation graphique de la série présente les caractéristiques suivantes :

Une tendance a la hausse avec des valeurs áuctuant autour de 4, 4.E ) 0 8 et 9.E ) 0 8 . Une non stationnarité en moyenne, témoignée par la tendance .

Un mouvement périodique caractérisé par des áuctuations ascendantes et descendantes tout au long de la période allant de Janvier 1997 a Décembre 20 0 4.

b-Examen du correlogramme de la serie O Et

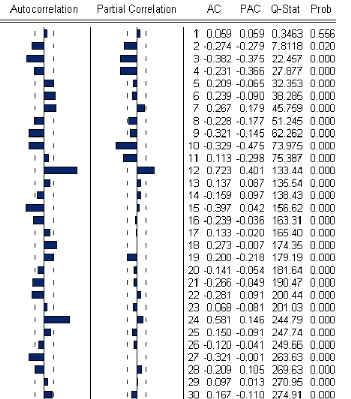
FIG.II.2ó Corrélogramme de la série O Et

Les corrélogrammes simple et partiel font apparaÓtre un "pic" important au retard k 6 12

ce qui laisse supposer que la série est a§ectée díune saisonnalité et par suite nous poussera a dire quíelle est non stationnaire, cíest ainsi quíun recours au test de Fisher nous permettera

de verifer nos hypothèses.

^{Etude de la saisonnalite de serie O E}t

Source des variations	SO	d.liberté	M O	F	P _o b	F critique
Lignes	1950 1.5	11	10 5 4.7	4.3 4	1.03 E 03	1.8 7

Le test confrme nos doutes concernant la présence díune saisonnalité puisque F 6 6.64 >

F ^{0 ) 05}

11 6 1.8 7.On procède a la désaisonnalisation de série par líapplication de líopérateur de

di§érence saisonnière V S 6 (1 B¹² ), líopération e§ectuée, la nouvelle série générée est

O ESAt

Analyse preliminaire de la serie O ESAt

Examen du correlogramme de la serie

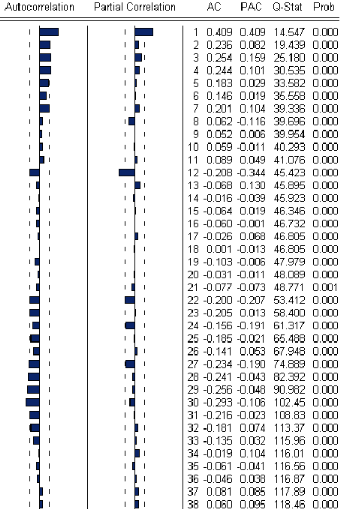
^{FIG.II.3ó Corrélogramme de la série O ESA}t

Líanalyse du correlogramme simple et correlogramme partiel de la serie O ESAt (Fig.l l .3 ) nous indique prealablement que la serie est non stationnaire, puisque la fonction díautocor- relation (visible sur la colonne AO ) ne decroÓt pas de manière rapide. Afn de verifer cette hypothèse, il convient díappliquer le test de racine unitaire.

Test de racine unitaire (Dickey-Fuller) sur la serie O ESAt

A partir du logiciel EVIEWS 4.0, on procède a líestimation par la methode des moindres carrees avec p 6 0 des trois modèles [ 4] , [ 5 ] , [ 6] de DickeyñFuller sur la serie O ESAt (car les residus forment un bruit blanc), dont les resultats díanalyse sont representes ci-dessous

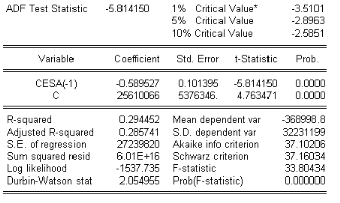
, 9 6 7 8 7 [ % ] A O ESAt 6 b O ESAt 1 ) O ) b t ) 6 t

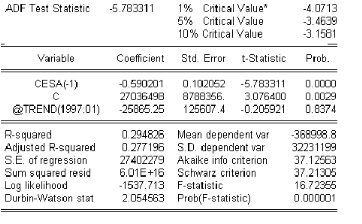
A la lecture de tableau ci dessus, on remarque que la statistique t' 6 5 .78 est inferieure

aux di§erentes valeurs critiques relatives aux seuils 1% , 5 % et 10 % : Líhypothèse H0 est rejetee, donc la serie O ESAt ne possède pas de racine unitaire, elle est donc stationnaire.

La probabilite de nullite du coecents cient de la tendance 0 .83 74 est superieure au seuil de 5 % , aussi la valeur empirique de la statistique de Student relative a la tendance(7 T REN D)

qui est egale a 0 .20 5 9 est inferieure aux valeurs tabulees (1.95 ) au seuil 5 % et (1.64) au seuil 10 % . On accepte donc, líhypothèse du nullite du coecents cient de la tendance (il níest pas signifcativement di§erent de zero), le processus níest pas de type T S (trend stationnary).De

la on estime le modèle [ 5 ]

, 9 6 7 8 7 [ $ ] A O ESAt 6 b O ESAt 1 ) O ) 6 t

Contrairement a la tendance, la probabilite de nullite de la constante est nulle et elle est inferieure au seuil 5 % , aussi la valeur empirique de la statistique de Student (t-statistic) relative a la constante O qui est egale a (4.763 4) est superieure aux valeurs tabulees (1.95 )

au seuil 5 % et (1.64) au seuil 10 % . On rejette donc, líhypothèse de nullite de la constante

(elle est signifcativement di§erente de zero).

Le fait que la statistique t' 6 5 .8 141 est inferieure aux di§erentes valeurs critiques relatives aux seuils 1% , 5 % et 10 % : líhypothèse H0 est rejetee, donc la serie O ESAt ne possède pas de racine unitaire, elle est donc bien stationnaire. Líestimation des paramètres sera entamee a la base du modèle[ 5 ] .

SpeciÖcation du modèle

Líanalyse du correlogramme partiel de la serie O ESAt (Fig.l l .3 ) montre quíaux retards

(k 6 1, 12, 22) les termes sont a líexterieur de líintervalle de confance et ce qui concerne le correlogramme simple, globalement, on remarque que les valeurs des fonctions díautocorrela- tion simples sont elevees au di§erents retards (k 6 1, 2, 3 , 4, 7, 12, 27, 28 , 29, 30 ....), ce qui nous amène a avoir plusieurs modèles candidats : SARM A(1, 1), SARM A(2, 0 ), SARM A(3 , 12), .. ect. Après une selection nous allons representer le modèle le plus adequat estime a líaide du logiciel EVIEWS 4.0 a savoir : SARl M A(p, Q , q ) x (P, D, Q ).

5.2.2 Estimation des paramètres

0 & / * , & (! , , ! " ) x ( , ! , ! )

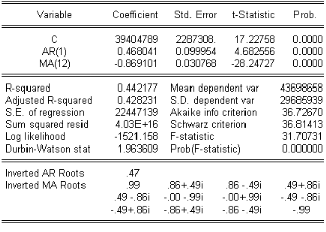
Remarque

1 Le modèle SARI M A(1, 0 , 12) x (0 , 1, 1) a été choisi, car il présente des critères de pouvoir prédictif meilleur que ceux des autres modèles estimés (a savoir : R² , R, statistique de Fisher : maximum ; et SSR, AI O , SO : minimum.

2 La statistique de Durbin-Watson 6 1.96, présage un bon ajustement.

5.2.3 Validation du modèle

Tests sur le modèle

Les racines des deux polynômes autoregressif et moyenne mobile sont supérieures en module

a 1, car leurs inverses calculés par EVIEWS sont tous inférieurs a 1, ainsi les conditions de stationnarité et díinversibilité sont vérifées.

Les composantes AR et M A de líARM A níont pas de racines communes (leurs inverses sont distinctes), il en résulte donc que notre représentation SARI M A(1, 0 , 12) x (0 , 1, 1) est minimale par le principe de parcimonie.

Tests sur les estimations

Les coecents cients des paramètres du modèle SARI M A(1, 0 , 12) x (0 , 1, 1) sont signifcative- ment di§érents de zéro, díailleurs le test de Student le confrme.

Test sur les residus

^{Representation graphique des series : residuelle (6} t^{), actuelle (O ESA}t^{) et estimee}

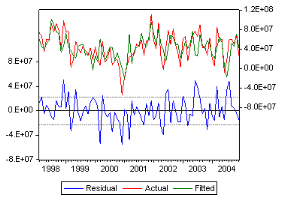
FIG.I I .4 Graphique des series estimee, reelle et celle des residus

Test de Ljung-Box

Le corrélogramme des résidus ne fait apparaÓtre aucun terme en dehors de líintervalle de confance au seuil 5 % , ce qui est confrmé par la Q s tat pour tout les retards en particulier

0 ) 05

Q s tat 6 25 .28 2 (au retard K 6 29) 0 x ²

(26) 6 3 8 .92, on peut donc assimilé les résidus

a un bruit blanc.

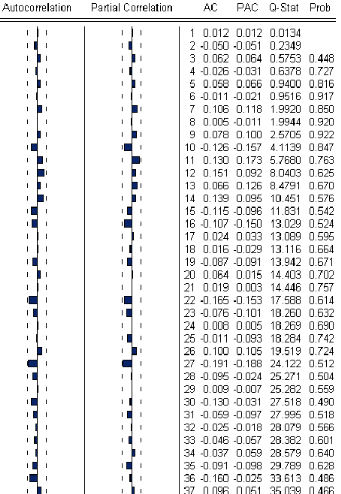
FIG.II.5 Oorrelogramme des residus

Líestimation du modèle SARI M A(1, 0 , 12) x (0 , 1, 1) est donc validée, la série G ESAt peut être valablement représentée par un processus de type SARI M A(1, 0 , 12) x (0 , 1, 1) et il síécrit :

^{G ESA}t ^{6 3 940 478 9 ) 0 .47G ESA}t 1 ^{) G ESA}t 12 ^{0 .47G ESA}t 13 ^{) t} t ^{) 0 .8 7t} t 12

Test de stabilite

Réestimons le modèle obtenu précédemment sur les 66 premières observations, cíest a dire sur la période (1997 : 0 1 20 03 : 0 6).

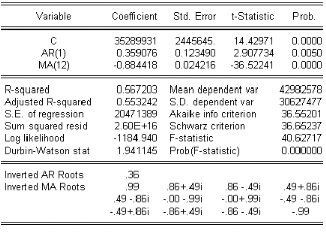
Les coecents cients du modèle sont signifcativement di§érent de zéro pour un seuil de 5 % (les valeurs empiriques t-statistic sont toutes supérieures aux valeurs tabulées au seuil 5 % ), et

les conditions de stationnarité et díinversibilité sont vérifées.

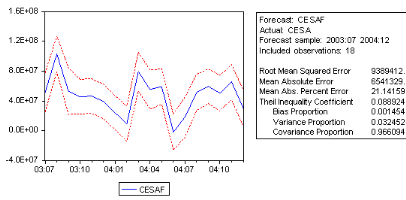
Fig.II.6.Graphe des previsions (C ESAF t) (0 7/ 20 03 12/ 20 0 4)

On remarque que les valeurs obtenues sont a líintérieur de líintervalle de confance, par

conséquent le modèle est stable.

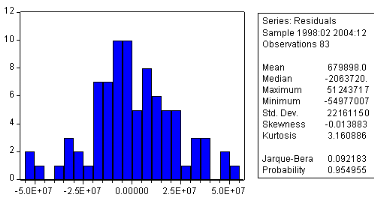
Test de normalite

Les tests sont e§ectués a partir des valeurs empiriques des coecents cients de Skewness, Kurtossis

et la statistique de Jarque-Berra données par le logiciel EVIEWS. En utilisant le logiciel on

a líhistogramme suivant :

^% (Bk )1/ 2 ^%

^{Test de Skewness : (B}K ^{)1/ 2 6 0 .0 1 ' 7} 1 ^{6 %}

ku 3

^%

^A

6

,3

6 0 .33 88 < 1.96.

^{Test de Kurtossis : k}u ^{6 3 .16 ' 7} 2 ⁶

^A 24

,3

6 0 .2975 < 1.96.

Donc, díaprès le résultat du test, nous acceptons líhypothèse de normalité en ce qui concerne

la symétrie et líaplatissement de la distribution, ce qui est confrmé par la statistique de

Jarque-Berra :

J B 6

83

6 ^{BK )}

83

0 ,05

(ku 3 )² 6 0 .0 9 < x ²

²⁴

(2) 6 5 .911.

Conclusion : Les résidus forment un bruit blanc gaussien.

5.2.4 Prevision

Líéquation du modèle BARI M A(1, 0 , 12) x (0 , 1, 1) représentant la série C EBAt est don-

née par :

O ESAt 6 3 940 478 9 ) 0 .47O ESAt 1 ) O ESAt 12 0 .47O ESAt 13 ) t t ) 0 .8 7t t 12

Les prévisions seront calculées a líaide de líEVIEWS pour un horizon h 6 12 mois depuis líorigine 12/ 20 0 4

Soit O^\ESAt(h) la prévision a líorigine t, a un horizon h :

Pour h 6 1 :

^X

O^\ESAt(1) 6 3 940 478 9 ) 0 .47O ESAt ) O ESAt 11 0 .47O ESAt 12 ) 0 .8 7t t 11

.

^X

O^\ESAt(12) 6 3 940 478 9 ) 0 .47O^\ESAt(11) ) O ESAt 0 .47O ESAt 1 ) 0 .8 7t t

Pour h > 12 :

O^\ESAt(h) 6 3 940 478 9 ) 0 .47O^\ESAt(h 1) ) O ESAt+ h 12 0 .47O ESAt+ h 13

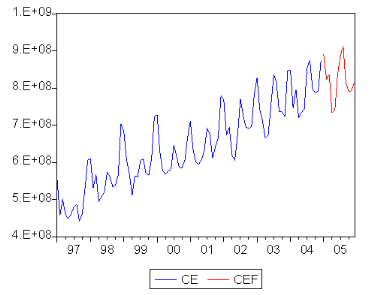
Fig.II.6-Graphe des previsions de la consommation des centrales electriques

Les prévisions sont données dans le tableau suivant :

Mois	Previsions (m ^3)
Jan	8 905 6640 1
Fev	8 24114942
Mar	83 60 73 93 4
Avr	73 38 03 203
Mai	740 4700 3 1
Jui	83 53 45 929
Juil	88 5 95 9278
Aou	913 7777162
Sep	8 140 77793
Oct	7915 9475 2
Nov	7925 5 73 97
Dec	8 15 78 78 2649