Section II :
Estimation de l'impact de la certification sur le bien être des
employés du secteur forestier au Cameroun
Dans cette section, il sera question de procéder
à l'estimation proprement dite, ensuite, à l'analyse de
l'influence des coefficients associés aux variables exogènes.
Puisque la valeur des coefficients n'a aucune signification économique,
un examen des effets marginaux pourra suivre pour la complétude de
l'analyse.
II.1 Méthode d'estimation
L'estimation des données qualitatives nécessite
le recours à des méthodes plus appropriées.
II.1.1 : Limites des méthodes
linéaires d'estimation
L'inadéquation de l'estimation des variables par les
méthodes linéaires peut être justifiée par plusieurs
raisons :
premièrement, étant donné que le codage
des réponses qualitatives se fait de façon arbitraire, les
valeurs des coefficients â sont nécessairement différentes
de celles obtenues pour tout autre codage, elles seraient par exemple
áâ si le codage était de type (0, á) par
conséquent, le paramètre â n'est pas
interprétable ;
Deuxièmement, une étude graphique montre que
l'approximation linéaire est peu adaptée au problème
posé. Considérons pour cela le modèle linéaire avec
une seule variable explicative (K = 1), notée X1i ,
et une constante. On pose ç = (ç 0,
ç 1) le bien être s'explique comme le suivant
:
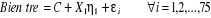
Nous pouvons constater l'inadéquation de ce
modèle à reproduire correctement la variable endogène
dichotomique Bienêtre i par un ajustement
linéaire.
Fig 4.1: Ajustement Linéaire de la Variable
Dichotomique Bienêtre (de notre étude)
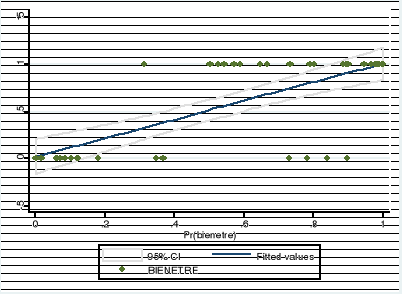
Source : construit par l'auteur à
partir des données d'enquête via le logiciel STATA 9.
Du fait du statut dichotomique de la variable endogène,
le nuage de points ainsi obtenu se situe soit sur la droite Bienêtre
= 0, soit sur la parallèle Bienêtre = 1. Ainsi,
comme on l'observe sur la figure 4.1, le nuage de points
associés à la variable endogène dichotomique
Bienêtre de notre étude est réparti sur deux
droites parallèles. Il est visiblement impossible d'ajuster ce nuage de
points de façon adéquate, par une seule droite ;
troisièmement, les variables qualitatives, posent un
certain nombre de problèmes mathématiques liés aux
hypothèses traditionnelles. Nous pouvons en retenir trois :
1. la variable Bienêtre ne pouvant prendre que
les valeurs 0 ou 1, la spécification linéaire implique que la
perturbation åi ne peut prendre, elle aussi, que 2 valeurs,
conditionnellement au vecteur Xi :
åi = 1- Xi ç avec
une probabilité de pi = Prob (bienêtre i
= 1) et
åi = - Xi
ç avec une probabilité de 1 - pi.
Ainsi, la perturbation åi du modèle
admet nécessairement une loi discrète, ce qui exclut en
particulier l'hypothèse de normalité des résidus.
2. lorsque l'on suppose que les résidus
åi sont de moyenne nulle, la probabilité pi
associée à l'événement Bienêtre
i = 1 est alors déterminée de façon
unique. En effet, écrivons l'espérance des résidus :
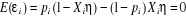
On en déduit immédiatement que : 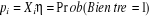
Ainsi la quantité 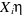 correspond à une probabilité et doit par
conséquent satisfaire un certain nombre de propriétés et
en particulier appartenir à l'intervalle fermé [0, 1]. Or rien
n'assure que de telles conditions soient satisfaites par l'estimateur des
Moindres Carrés utilisé dans le modèle linéaire. Si
de telles contraintes ne sont pas assurées, le modèle correspond à une probabilité et doit par
conséquent satisfaire un certain nombre de propriétés et
en particulier appartenir à l'intervalle fermé [0, 1]. Or rien
n'assure que de telles conditions soient satisfaites par l'estimateur des
Moindres Carrés utilisé dans le modèle linéaire. Si
de telles contraintes ne sont pas assurées, le modèle
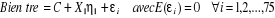 n'a pas de sens. n'a pas de sens.
3. Enfin, même si l'on parvenait à assurer le
fait que les propriétés évoquées ci-dessus soient
satisfaites par l'estimateur des Moindres Carrés des paramètres
du modèle linéaire, il n'en demeurerait pas moins une
difficulté liée à la présence
d'hétéroscédasticité. En effet, la matrice de
variance covariance des résidus varie entre les individus en fonction de
leurs caractéristiques associées aux exogènes xi
puisque :
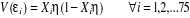
Or, de plus ce problème
d'hétéroscédasticité ne peut pas être
résolu par une méthode d'estimation des Moindres Carrés
Généralisés tenant compte de la contrainte liée
à l'intervalle [0, 1] puisque la matrice de variance covariance des
perturbations dépend du vecteur â des paramètres à
estimer dans la spécification linéaire, qui est par nature
supposée inconnue.
Etant donné que les modèles
énumérées ci-dessus sont à probabilité non
linéaire, et que l'estimation par les MCO est problématique, la
méthode alternative la plus usitée lorsque la loi des
perturbations est connue est la méthode du maximum de vraisemblance.
| 


