Compression d'images fixes: comparaison des méthodes par transformations en ondelettes et celle par curvelets

CONCLUSION

L'utilisation des ondelettes de Haar permet donc de nombreuses applications au niveau de la compression d'images et de signaux. D'autres familles d'ondelettes sont utilisées actuellement, elles offrent de meilleurs résultats de compression. Elles sont suffisantes pour comprendre le principe de compression par ondelettes. L'algorithme que nous avons utilisé est plus performant que le standard JPEG, qui compresse la taille d'une image par 20 en moyenne alors que la méthode par ondelettes compresse en moyenne par 50 : cas du JPEG 2000

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 31

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

~~~~~~~~

~~~~~~~~ IV ~~~~~~~~~~~

~~~~~~~~ ~~~~~ ~"~~

~"~~ ~5

~IGNA5 EN 5

5

5

~~~~~~~~ ~~~~~ 68,

~"~~~~~~

~ 5 ~~~~~~~~~~~ ~"~~~~~~

⁶⁸

INTRODUCTION

Depuis leur introduction au début des années 1980, les ondelettes ont fait l'objet de beaucoup d'attention dans des domaines aussi diversifiés que le débruitage, la compression, la détection des discontinuités et des pics, l'imagerie médicale ou satellitaire . . . Elles y ont démontré leur force, mais les ondelettes séparables sont isotropes et ne peuvent donc pas capturer, par exemple, la régularité d'un contour dans une image. Ceci est du au fait que les ondelettes sont des outils adaptés à la description des discontinuités de signaux mono dimensionnels et que cette propriété n'est plus vraie pour des dimensions supérieures. En particulier, l'orthogonalité de la décomposition et l'échantillonnage critique font apparaitre des effets d'aliasing visibles autour des contours. De plus, le nombre d'orientations est limité et fixe, et les contours sont redondants d'un niveau de résolution à un autre, ce qui requiert un grand nombre de coefficients d'ondelettes pour les représenter.

Afin de pallier à ce problème, de nouvelles décompositions multi-résolutions mieux adaptées à la représentation de tels signaux ont été introduites. Nous présenterons dans ce chapitre la description de l'une d'entre elle qu'est la transformée en Curvelets en vue d'une compression d'images fixes.

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 32

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 33

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I. LA TRANSFORMEE EN CURVELETS

Dans le domaine du discret et en particulier pour le cas des images, on peut considérer que de manière locale, on trouve des contours rectilignes. C'est ce qui conduit à la création de la transformée en Curvelets. Cette transformée est obtenue en deux grandes étapes. Tout d'abord on partitionne l'image en carrés de tailles variables avec recouvrement pour éviter les effets de bord. Ces carrés sont obtenus grâce à une fenêtre de Fourrier à support fini. Au sein de ces carrés on applique une transformée en Ridgelets discrète avec une dilatation de la fonction d'onde de 1/a². Les contours non capturés par l'analyse en ondelettes séparables se retrouvent dans les sous-bandes de détails. Un partitionnement suffisamment fin des sous-bandes permet alors d'obtenir des blocs où ces contours forment des lignes droites et sont donc adaptés à l'analyse en Ridgelets. La transformée en Curvelets est inversible mais redondante car l'analyse en Ridgelets discrète sous-jacente est réalisée au moyen d'une FFT2 du plan polaire, nécessitant plus de points que ceux disponibles dans la grille rectangulaire. Le choix d'utilisation de la FFT provient essentiellement du théorème de la projection de Fourrier (Fourier Slice Theorem). En effet, celui-ci indique que la transformée de Radon peut être obtenue en appliquant une transformée de Fourier inverse 1-D le long des lignes radiales passant par l'origine dans le domaine de Fourier 2-D de l'image.

Toutes ces étapes sont illustrées sur la figure suivante :

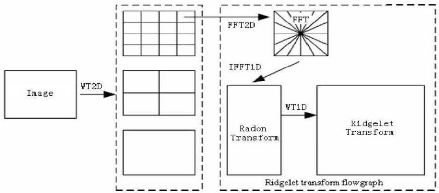
Figure 9 Schéma de construction de la transformée en Curvelets d'une image

Rapport Rédigé et présenté par SIMO TEGUEU et EMBOLO AURELIEN Page 34

CHAPITRE IV : DECOMPOSITION D'UN SIGNAL EN CURVELETS : APPLICATION A LA
COMPRESSION D'IMAGES FIXES

I.1 TRANSFORMEE EN CURVELETS DICRETES

Nous allons aborder le fonctionnement de la transformée en Curvelets de façon plus détaillée que le point de vue présenté ci-dessus.

Dans le domaine continu, et donc dans notre cas si l'on travaille dans R², il faut considérer deux fenêtres pour décrire les Curvelets. La première fenêtre est une fenêtre radiale W(r), la seconde est une fenêtre angulaire avec les coordonnées polaires r et t dans le plan fréquentiel. Ces fenêtres sont des fonctions régulières à valeurs réelles strictement positives. Les ensembles de départs de ces fonctions sont respectivement r y [1/2,2] pour W et t y [-1,1] pour V. Ces fenêtres doivent toujours respecter les conditions d'admissibilité suivantes :

?01 E -,1 (2-$) = 1 ,$ \ p oeù, 2 {

?01 Y ú~,1 ~*~·~~1,*\ ~ ~ ~ , ~ ~ É ;

Nous pouvons alors définir une fenêtre fréquentielle Uj pour tout j ç j0 dans le domaine de Fourier.

-($,) = 2,

cents£ EU2^,-$VY~^~£/: ~~ )

qui dépend à la fois de l'échelle et de la direction. En rendant symétrique l'Erreur : source de la référence non trouvée afin de couvrir toutes les orientations possibles, C'est-à-dire Uj(r,?)+Uj(r,?+%), on obtient des valeurs réelles de Curvelets. Ces bases posées, il faut transférer ces différents résultats dans le domaine du discret. Le problème est que la fenêtre Uj fournit une analyse fréquentielle régulière le long de la couronne dyadique 2- OE $ OE 2-⁰¹ et de l'angle - %. 2,-/2 OE OE %.2^,-/² et que cela s'adapte difficilement sur les grilles Cartésiennes. Candès et al. proposent donc une nouvelle formulation de la couronne basée non pas sur des cercles comme sur la Figure (a) mais sur des carrés concentriques et des cisaillements comme sur la Figure (b). Dans cette nouvelle formulation l'analogue Cartésien de la famille ( E- )-«o telle que