CHAPITRE II : DE L'ANALYSE DE FOURRIER A L'ANALYSE PAR
ONDELETTES
CONCLUSION
Nous avons vu comment, de l'analyse de Fourrier, en passant
par l'analyse de Gabor, nous sommes aboutis à l'analyse par ondelettes.
La transformée de Fourrier malgré ses inconvénients a
connu un succès dans plusieurs domaines d'applications (compression des
images à travers la norme JPEG, le débruitage des signaux et
plusieurs autres domaines) et, doit son succès à sa
capacité à bien décrire un grand nombre de signaux (tous
les signaux stationnaires en fait) et à être implantée dans
un système réel très efficacement. La transformation en
ondelettes, elle aussi, a connu un grand succès qui repose sur le
même type d'arguments. Précisons ici que la transformée en
ondelettes a une ambition bien plus grande que celle de la transformée
de Fourrier car la classe des signaux qu'elle vise à décrire,
c'est-à-dire les signaux non stationnaires, est d'une bien plus grande
diversité mais demeure dans certains cas moins efficace. Une
particularité fondamentale pour classer les ondelettes est leur
degré de redondance. La transformée en ondelettes continue est
par construction très redondante mais la transformée en
ondelettes discrète peut ne pas l'être et l'absence de redondance
est même recherchée dans des applications comme la compression
d'images.
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR
: APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
~~~~~~~~
~~~~~~~~
~~~ :
7ASES D"ONDE5ETTES ORTHOGANA5ES DE HAAR
7 5 5 ~~ ~~~~
5 ~ 5 ~~~~~~~~~~~ ~"~~~ ~~~~~ 68
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 25
Nous avons vu au chapitre précédent qu'il existe
plusieurs familles d'ondelettes caractérisées chacune par
l'ondelette mère ip(t). Le tableau1 présente les plus
courantes et leurs spécificités. Pour évaluer la
transformée en ondelettes dans le domaine de la compression d'images
fixes, notre choix porte sur l'analyse par ondelettes de Haar.
Le choix de l'ondelette résulte en fait d'un compromis
entre son support et son nombre de moments nuls ; plus son support est petit,
moins nombreux seront les gros coefficients affectées par une
irrégularité d'un signal. D'un autre côté, prendre
une ondelette avec beaucoup de moments nuls permet d'avoir des coefficients de
petites échelles sur les parties régulières du signal. Or
favoriser l'une de ses propriétés se fait au détriment de
l'autre.
INTRODUCTION
Dans ce chapitre, nous nous restreignons à
l'étude des ondelettes orthogonales qui sont un cas particulier des
ondelettes discrètes. Ce type d'ondelettes est extrêmement utile
en pratique car les ondelettes orthogonales sont non redondantes (la non
redondance est à la fois bénéfique pour la rapidité
de calcul de la transformation et pour les performances en terme de taux de
compression) et leur inversibilité est assurée. Dans le chapitre
précédent nous avons vu qu'il est "facile" de construire une
transformation en ondelettes continue puisqu'il il suffit de trouver une
fonction de moyenne nulle (l'ondelette mère). Par contre, il est
beaucoup plus difficile de trouver des ondelettes orthogonales. Les travaux
pionniers dans cette recherche sont ceux de J. Strömberg (1981) et ceux de
Y. Meyer (1985). Dans ces travaux, des exemples de bases d'ondelettes
orthogonales sont proposées mais aucune méthode
générique pour trouver de telles bases n'a alors
été proposée. C'est précisément là
que l'analyse multirésolution (AMR) entre en scène. L'une des
vertus de l'analyse multirésolution est de produire "facilement" des
bases d'ondelettes orthogonales. C'est en voulant expliciter le lien entre les
algorithmes pyramidaux du traitement d'image et la théorie des
ondelettes que Stéphane Mallat a mis au point l'analyse
multirésolution. Deux autres vertus de l'AMR est qu'elle est très
adaptée à décrire certaines situations physiques telles
que celles rencontrées en
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 26
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
traitement d'image où l'information est répartie
à des échelles qui peuvent être très
différentes, et elle se prête naturellement à une
implantation rapide.
I. ANALYSE MULTIRESOLUTION
Soit un ensemble de sous-espaces de L2(R)
(l'ensemble des signaux à énergie finie) tel que : ...c V2 c V1 c
V0c V-1c...c Vj+1 c Vjc...
GGGGGGGGj = L2 (f)
U J Ev Vn ; E` V j = 0
V j E Z , f (x) E Vj = f (2-1 x) E Vj+1
V k E Z , f (x) E V0 = f ( x -- k) E V0
Ces propriétés définissent une analyse
multirésolution sur L2(R).
L'analyse multirésolution a été
définie par Mallat. L'idée est de projeter un signal f(t) E
L2(R) appartenant à un espace Vj sur un sous-espace
Vj+1 et un sous-espace Wj+1 dans le but de réduire
la résolution de moitié. Le schéma est donné en
figure ci-dessous. Il existe donc deux opérateurs de projection Aj et Dj
qui projettent respectivement le signal f(t) sur Vj+1 et
Wj+1. Vj+1 est le sous-espace d'approximation et Wj+1 le sous-espace
de détails. On peut démontrer qu'il existe une fonction
d'échelle =(t) E L2(R) qui engendre par dilatation et
translation une base orthonormée de Wj+1. Les espaces obtenus
ne sont pas quelconques, ils possèdent des propriétés
intéressantes. Par construction, les espaces d'approximation
Vj+1 et de détails Wj+1 sont supplémentaires : Vj =
Vj+1g Wj+1.
V0
V3 W3
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
Les fonctions de bases dilatées sont données par
les relations : (Di,n(t)=2-i/2(D(2-it-n) avec
nEZ et yri,n(t)=2-i/2yr(2-it-n) avec nEZ .
On a donc Aif= < f, (Di,n> (Di,n et Dif=?n <
f, yrin > yri,n où < f(t), g(t) > désigne le produit
scalaire n de f(t) par g(t) : < f(t), g(t) > = f00 0000
f(t)g(t)GGGGGGdt
Puisque les fonctions utilisées appartiennent toutes
à L2(R), on a g(t)GGGGGG=g(t). On pose
ai,n= < f, (Di,n> et di,n= < f,
-th,n >. ai,n et di,n sont
respectivement les coefficients d'approximation et de détails de la
transformation en ondelettes de la fonction f.
I.1 APPLICATION DE L'AMR A L'ALGORITHME D'ANALYSE DE HAAR
POUR
DECOMPOSITION D'UNE IMAGE
Les ondelettes de Haar
Considérons un signal échantillonné
régulièrement sur [0;1] en 2P points, on note ces
points
|
xk =
|
z On associe à cet échantillon une fonction f
définie par f (x)= (fk si x E [xk; xk+1[ k
0 sinon
|
Quand cet échantillonnage varie, la fonction f
décrit l'ensemble Ep des fonctions constantes sur chacun des
intervalles, et nulles en dehors de l'intervalle [0,1[. Ep est un
sous-espace vectoriel de l'espace vectoriel des fonctions réelles
à valeurs réelles. De plus, quand on fait varier p, les espaces
Ep sont emboîtés, c'est à dire que E0 c E1 c...c
EP+1 c.... Leur réunion est donc encore un sous-espace
vectoriel E de l'espace vectoriel des fonctions réelles à valeurs
réelles.
On munit l'espace vectoriel E du produit scalaire
définit par : (fIg) = fô f(x)g(x)dx Pour obtenir une base de
Ep, il suffit de considérer les fonctions
(pp,kdéfinies par :
(pp,k :l (pp,k(x) = 0 sinon
(pp,k(x) = 1 si x E [xk ; xk+1]
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 27
En effet, par définition même de Ep,
toute fonction f de Ep se décompose de façon unique
sous la forme. f = EXp o1 fk(pp,k. Ces fonctions (pp,k peuvent
s'écrire sous la forme (pp,k (x) =(p(2pX - K), où (p
est définie par (p :
(p(x) = 1 si x E [0;1[
(p(x) = 0 sinon
Cette base est orthogonale, en effet on remarque que
((pp,kI(pp,k')=0 si k ? k' et
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 28
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
}vw,l~vw,l'= m ~ et. Il s'ensuit que la base des
vw,lest orthogonale. Les espaces Ep sont alors
des espaces euclidiens. On considère le
supplémentaire orthogonal Fp de Ep dans
Ep+1. Ainsi on a Ep = E1 € F0 € ...€
Fp-1 pour tout p. Cette décomposition sert à
définir la tendance grossière d'un signal E0, et ses
détails à des résolutions de plus en plus fines
(F0,F1,...).
Algorithme de calcul des coefficients des ondelettes de
Haar
L'ondelette mère de Haar est la fonction définie
par :
~
1 si x \ p0 ; ~É
Ø(x)=-1 si x \ ~ ;1{
~
0 sinon
A partir de cette fonction, on définit les fonctions
Øp,k par Øp,k = Ø(2px-k) De même que dans le
paragraphe précédent, }vw,l~øw,là = 0 si
k ? k' et, }vw,l~øw,l = 0 car fol (2wx - e)
ø(2x - k)dx = 0. On en déduit que la famille qui réunit
les vw,let lesøw,l(0 OE e OE 2w - 1) est une base orthogonale
de Ep+1, donc les Øp,k forment une base orthogonale de
l'espace Fp de Ep dans Ep+1 et on a le
résultat fondamental suivant :Pour tout pç 1, la famille
~øw,l~~élé~m0~est une base orthogonale de Fp.
De plus, }øw,l~øw,l = ~ 2m. Nous pouvons désormais
calculer les coefficients d'ondelettes associés à un signal
sp y Ep. Il
se décompose sous la forme s(p) = ? Fw,lvw,l
m, . Puisque Ep = Ep-1 € Fp-1, sp se
décompose
l,~
~mèê ~mèê
en sp = sp-1+ dp-1 avec sp-1 = ?
Fw,~,lvw,~,l et dp-1 = ?
Fw,~,lvw,~,l
l l
Pour les mêmes raisons, }vw,l~vw,1,l' = 0 et
}vw,l~øw,1,l' = 0 si x ' «2kN, 2kN + 1»
et
}vw,l~vw,~,l' = m ~ et }vw,l~øw,~,l' ~ m
~,~~ï si x ' «2kN, 2kN + 1».
Ceci permet de déterminer facilement la
décomposition de sp y Ep sur la base des
vw,1,l et øw,1,l. En effet, si sp =
sp-1+ dp alors l'orthogonalité de la base implique
~mèê ,~
}sw~vw,~,l = -èê,
~èê et }sw~øw,~,l =
™èê,
~èê . La décomposition s(p) = ? Fw,lvw,l et
les
l,~
valeurs des produits scalaires donnent alors
}sw~vw,1,l = -,:0-,:ê
~ et
-,:,-,:ê'-,:0-,:ê
-,:,-,:ê
}v,z~ø,1,z = 2 , doù s,1,z =
2 et d,1,z = 2
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 29
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
L'intérêt est que l'on passe d'un
échantillon de taille 2p à un échantillon
principal de taille 2p-1 et un échantillon de taille 2p-1 en
utilisant que des sommes ou des différences.
Compression ou Approximation d'un signal 1D selon l'algorithme
de Haar
Principe
Si le signal est régulier, les valeurs des
échantillons successifs seront proches. Les coefficients de
détails issus de la différence de deux valeurs
consécutives de l'échantillon seront donc petits. En s'imposant
une précision F, on ne gardera que les coefficients d'ondelettes
supérieurs en valeur absolue à F.Ceci permet une compression du
signal.
Voici l'algorithme utilisé : on reçoit un signal de
la forme s(p) = ? Fw,lvw,l
m, , on le
l,
décompose en sp = sp-1+ dp-1 et on transforme
dp-1 en dGp-1, dGp-1 =
? ~mèê,~ dG p-1,køw,1,l avec
dGp-
l,~
1,k = dp-1,k si ~d,l,z~ ç F et
dp-1,k = 0 sinon . On recommence ensuite le procédé
avec le signal sp-1.
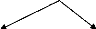
87.015% de coef à zéro
70.736% de coef à zéro
Figure 6 Compression d'un signal 1D sous MATLAB selon
l'algorithme de Haar
Rapport Rédigé et présenté par SIMO
TEGUEU et EMBOLO AURELIEN Page 30
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
Décomposition et approximation d'une image selon
l'algorithme de Haar Présentation de l'algorithme
Une image en noir et blanc peut être
considérée comme un ensemble de pixels, chaque pixel
représentant un niveau de gris. On peut modéliser cette image par
une matrice carré de taille égale à la résolution
de l'image. Pour une image en couleur, il suffit de considérer trois
images, chacune représentant le niveau de rouge, de vert et de bleu de
l'image originale.
Pour mettre en application la méthode de Haar on
pourrait considérer la matrice comme un échantillonnage en
mettant ses lignes bout à bout. Cependant on perd le lien avec les
colonnes. Il est donc plus efficace d'appliquer l'algorithme de Haar aux lignes
de la matrice puis à ses colonnes. Cet algorithme de
différentiation-sommation se traduit par la multiplication matricielle
à l'aide d'une matrice contenant beaucoup de 0.
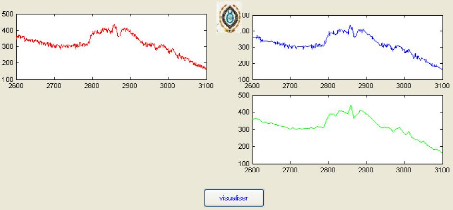
La décomposition d'un signal 2D tel qu'une image selon
l'AMR ce présente comme suit :
Figure 7 Analyse Multirésolution
CHAPITRE III : BASES D'ONDELETTES ORTHOGONALES DE HAAR :
APPLICATION A LA COMPRESSION D'UNE IMAGE FIXE
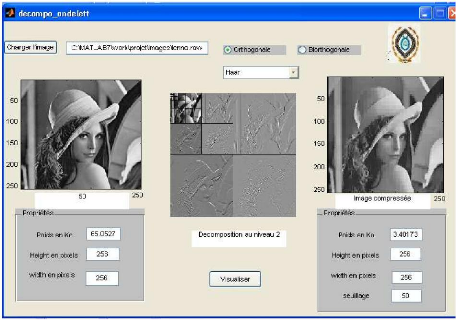
Figure 8 Décomposition et approximation de l'image de
lenna sous MATLAB selon Haar
| 


