2.2. Etude descriptive des
séries utilisées
Les rendements ont depuis longtemps été
considérés comme suivant une distribution normale. Or, la
prétention erronée à cette loi, a conduit certains travaux
à des résultats non fiables, que ce soit pour la prévision
des valeurs futures des rendements que pour les décisions
d'investissement. En observant quelques études antérieures la
plupart des travaux traitant du sujet des rendements boursiers ont
rejeté l'hypothèse de la normalité.
Il convient aussi d'étudier les caractéristiques
stochastiques avant de traiter une série chronologique et ce afin de
déterminer la stationnarité des séries, le degré de
modification de son espérance et sa variance dans le temps.
2.2.1. Normalité des séries
Pour déterminer les caractéristiques du
modèle à estimer, il est nécessaire d'étudier les
propriétés statistiques des séries. En effet les
distributions des séries de rentabilité ont été,
pendant longtemps, considérées comme suivant une loi normale.
Pourtant, quelques études sur ces séries ont montré que
leurs distributions ne sont pas normales. Ces distributions sont souvent
asymétriques et affichent un leptokurtosis. Elles sont souvent plus
épaisses aux extrémités et font apparaître des
« queues épaisses ».
La normalité des rentabilités est
vérifiée par des tests économétriques qui se basent
sur la détermination des coefficients de symétrie (Skewness) et
d'aplatissement (Kurtosis) et la statistique de Jarque et Bera qui
synthétise les deux propriétés.
a.
Présentation des tests
i.
Test de Skewness
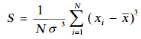
Skewness est une mesure de l'asymétrie de la
distribution d'une série autour de sa moyenne, c'est le moment
centré d'ordre 3. Un Skewness supérieur à la valeur
critique qui est 0 indique que la distribution présente une
asymétrie vers la droite, alors qu'un Skewness < 0 implique que la
série est asymétrique vers la gauche. La formule de Skewness se
présente comme suit
ii. Test de Kurtosis
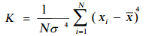
Afin de mesurer l'aplatissement des séries, nous
pouvons recourir à une comparaison des kurtosis k avec la valeur que
prend ce coefficient. La distribution est jugée normale lorsque (k=3).
S'il excède ce chiffre, la série est leptokurtique; elle est plus
pointue avec des queues de distribution plus épaisses que celle de la
loi normale. Sinon si (k<3), la distribution est platykurtique,
c'est-à-dire que celle-ci est plus aplatie que la distribution normale.
La formule de Kurtosis se présente comme suit :
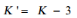
On exprime le degré d'excès de Kurtosis de la
façon suivante :
| 


