Conception et dimensionnement d'un pont en ba.

IV.1.2.3.2. Lignes d'influences des efforts tranchants

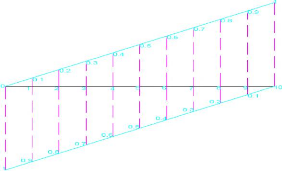
IV.1.3. Application

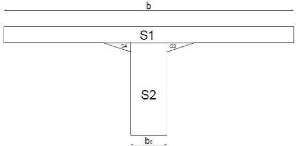
Déterminons d'abord la largeur de la table de compression :

Page 42 sur 115

b

		b0	= Min = Min = .4 = 2(	L Lx [ ] .11
b	2	b0		0' 2 [ 8 2.81
b	2	b0		.4)	0' 2 J
b	2	b0

b = 2.8 0.4 b = 3.20m

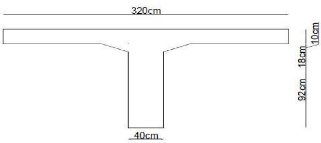
IV.1.3.1. Poids propre

a) Poutre

> Dalle (table de compression)

S = 0. 8 3.20 = 0.578m > Nervure

S2 = 0.40 .02 = 0.408m
> Les deux goussets

0. 0.3

S4 = S3 = 2		= 0.03m
	2

St = S S2 (S3 4) = 0.576 0.408 0.03 = .0 4m

D où Pp = St b = .0 4 25 = 25.35 KN m

¹¹ Pratique du BAEL 91, cours et exercices corrigés

Page 43 sur 115

b) Entretoise

Les effets des entretoises extrêmes sont directement reprisent par les appuis, les autres entretoises (intermédiaires) peuvent être considérées comme ponctuelles ou uniformément réparties ; nous considérons ce dernier cas :

Pentr =	Nentr be(he e de la dalle)(b b0) b
	L
Pentr =	2 0.35( .02 0. 8)(3.20 0.40)25	= 2.28KN
	2

Alors :

P = Pp Pentr

P = 2.28 25.35 = 27.6KN = 2.76t m IV.1.3.2. Surcharge fixe sur la moitié du pont > Garde-corps : 0,05t/m > Chape de protection : 0,15t/m
>	Revêtement asphalté :	7 0.03 2.3 = 0.483 t/m
>	Mortier de port : 0.0	.5	2.2 = 0.033 t/m
>	Sable (trottoir) : 0.	.5	.8 = 0.27t/m
>	Couche d'isolation : 7	0.02	2.3 = 0.322 t/m
>	Couche de forme : 7	0.04	2.3 = 0.6 4 t/m
>	Pierre de taille : 0. 5	0. 5	2.3 = 0.052 t/m
>	Dallette : 0.03 .5	2.2 =	0. 08 t/m

? = .79 ^t /_m

Etant donné que la moitié du pont comporte deux poutres, on aura comme solution :

.72 P = 2

= 0.895t/m

D'où Pt = P P = 2.76 0.895 = 3.66 t/_m en ELS Et Pt = 4.94 ^t /_m en ELU

IV.1.3.3. Foule

Charge positive : en ELS .44 t/_m et en ELU 2. 6 t/_m

Charge négative : en ELS 0. 5 t/_m et en ELU 0. 7 t/_m

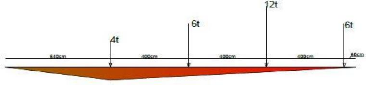
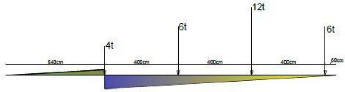
IV.1.3.3. Convois

Le convoi de 32t mis dans la position la plus défavorable. La position longitudinale de convois produit un moment maximum.

La norme NBN considère la charge suivant pour le pont route par rapport à la bande de circulation, un convoi routier de 32t (12t, 6t, 6t, 4t, 4t) ? Les essieux étant permutable et écartés de 4m

IV.1.3.3.1. Valeurs des moments dus au convoi

On calcul ces valeurs suivant la règle de triangle semblable en tenant compte du déplacement du convoi au long du pont.

Cas 1 où le convoi est fixe sur le pont Au point 1

/ .l v .	. = alors Y =			= 0.9 (4t)

/ .	/	. = alors Y2 =			= .3 (6t)

/ .	/	. = alors Y3 =			= 0.9 ( 2t)

/ .	/	. = alors Y4 =			= 0.5 (6t)

/ .	/	. = alors Y5 =			= 0. (4t)

s . .		. = alors Y =				= 0.8 (4t)
	. = alors Y2 =			= 2.6 (6t)

Page 44 sur 115

Au point 2

s .		. = alors Y2 =			= .8 ( 2t)

s .		. = alors Y4 =			= (6t)

s .		. = alors Y5 =			0.2 (4t)

Au point 3

s .		=
.		s .
=
.		s .
=
.		s .
=
.		s .
=

.

.

.

.

.

.

Au point 4

.

alors Y =

.

alors Y2 =

.

alors Y3 =

.

alors Y4 =

.

alors Y5 =

= 0.7 (4t)

= 3.5 (6t)

= 2.7 ( 2t)

= .5 (6t)

= 0.3 (4t)

.

/ .:

V .

= 0.6 (4t)

.

= alors Y =

.

/ .: V .

= 3 (6t)

.

= alors Y2 =

/ .	/	. = alors Y3 =			= 3.6 ( 2t)

/ .	/	. = alors Y4 =			= 2 (6t)

/ .	/	. = alors Y5 =		= 0.4 (4t)
	.		.

Page 45 sur 115

Page 46 sur 115

Au pont 5

? . alors Y = .

= = 2.5 = Y4 (6t)

? . alors Y2 = .

= = 0.5 = Y5 (4t)

? Y3 = 4.5 ( 2t)

IV.1.3.4.1.1. Tableau récapitulatif du moment

Section	4t			6t			12t		somm e	0.57M
	Y1	Y2	(Y1+Y2)4 t	Y1	Y2	(Y1+Y2)6 t	Y	12Y
	0.	0.
1	9	1	4	1.3	0.5	10.8	0.9	10.8	25.6	14.60
	0.	0.
2	8	2	4	2.6	1	21.6	1.8	21.6	47.2	26.9
	0.	0.
3	7	3	4	3.5	1.5	30	2.7	32.4	66.4	37.85
	0.	0.
4	6	4	4	3	2	30	3.6	43.2	77.2	44
	0.	0.
5	5	5	4	2.5	2.5	30	4.5	54	88	50.16
Somm										173.5
e			20			122.4		162	304.4	1

Cas 2 où le convoi se déplace sur le pont Au point 1

ü Y = .62 (4t)

ü . =

. .

alors Y2 = . . . = .22 (6t)

ü .

.

=

.

alors Y3 = . .

= 0.82 ( 2t)

ü .

.

=

.

alors Y4 = . .

= 0.42 (6t)

ü .

.

=

.

alors Y5 = . .

= 0.02 (4t)

Au point 2

ü Y = 2.88 (4t)

ü . = . .

alors Y2 = . .

. = 2.08 (6t)

ü . = . .

. . = .28 ( 2t)

alors Y3 =

ü .

.

=

.

alors Y4 = . .

= 0.48 (6t)

ü .

.

=

.

alors Y2 = . .

= 2.58 (6t)

ü .

.

=

.

alors Y3 =

. . = .38 ( 2t)

ü .

.

=

.

alors Y4 = . .

= 0. 8 (6t)

Page 47 sur 115

Au point 3

ü Y = 3.78 (4t)

Au point 4

ü Y = 4.32 (4t)

ü .

.

=

.

alors Y2 = . .

= 2.72 (6t)

ü .

.

=

.

alors Y3 =

. . = . 2 ( 2t)

Au point 5

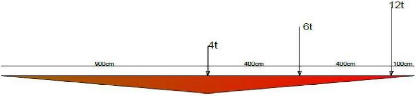
ü Y ü .	= = =	4.5 (4t) . Y2 alors =	=		2.5 (6t) 0.5 ( 2t)	ü .
ü		=

Pour les points :

P = P9; P2 = P8; P3 = P7; P4 = P6, vus que le diagramme est symétrique IV.1.3.4.1.2. Tableau récapitulatif

section	4t			6t			12t		somme	0.57M
	Y1	Y2	(Y1+Y2)4t	Y1	Y2	(Y1+Y2)6t	Y	12Y
1	1,62	0,02	6,56	1,22	0,42	9,84	0,82	9,84	26,24	14,96
2	2,88	0	11,52	2,08	0,48	15,35	1,28	15,36	42,24	24,08
3	3,78	0	15,12	2,58	0,18	16,56	1,38	16,56	48,24	27,50
4	4,32	0	17,28	2,72	0	16,32	1,12	13,44	47,04	26,81
5	4,5	0	18	2,5	0	15	0,5	6	39	22,23

Page 48 sur 115

somme

202,76

115,57

73,07

68,48

61,2

IV.1.3.4.1.3. Tableau synthèse des deux cas

Section	CAS 1		CAS 2		Mcrt	A RETENIR
	M	M*Mcrt	M	M*Mcrt
1	25,6	14,59	26,24	14,96	0,57	14,96
2	47,2	26,90	42,24	24,08	0,57	26,9
3	66,4	37,85	48,24	27,50	0,57	37,85
4	77,2	44,00	47,04	26,81	0,57	44
5	88	50,16	39	22,23	0,57	50,16
Somme		173,51		115,57		173,87

Comme nous venons de trouver les moments de fléchissant dus aux trains des charges de convoi, alors trouvons les moments dus à la foule et au poids propre de la poutre en fin de faire la sommation de tous les trois moments.

IV.1.3.4.1.4. Tableau des moments dus à la foule

Section	S+	q+ EN ELS	q+ EN ELU	q+S+ ELS	q+S+ ELU
1	14,58	1,44	2,16	21,00	31,49
2	25,92	1,44	2,16	37,32	55,99
3	34,02	1,44	2,16	48,99	73,48
4	38,88	1,44	2,16	55,99	83,98
5	40,05	1,44	2,16	57,67	86,51

Page 49 sur 115

Page 50 sur 115

IV.1.3.4.1.5. Tableau des moments dus au poids propre

Section	S+	Pt	Pt'	S+Pt	S+Pt'
1	14,58	3,66	4,94	53,36	72,03
2	25,92	3,66	4,94	94,87	128,04
3	34,02	3,66	4,94	124,51	168,06
4	38,88	3,66	4,94	142,30	192,07
5	40,05	3,66	4,94	146,58	197,85

IV.1.3.4.2. Valeurs des efforts tranchants dus aux convois

L'effort tranchant est maximal aux appuis et on peut le calculer toujours suivant la règle de triangle semblable en tenant compte du déplacement du convoi tout au long du pont.

Cas 1 où le convoi est fixe sur le pont Au point 0

? olrs Y0 =

= = 0.94 (4t)

? lors Y =

= = 0.72 (6t)

? alors Y2 =

= = 0.5 ( 2t)

? alors Y3 =

= = 0.27 (6t)

? alors Y3 =

= = 0.05 (4t)

Page 51 sur 115

Au point 1

Nous appliquons la même procédure, et on a des valeurs :

1' Y0 =		0 (4t)
1' Y	=	0.72 (6t)
1' Y2	=	0.5 ( 2t)
1' Y3	=	0.27 (6t)
1' Y4	=	0.05 (4t)

Au point 2

1'	Y0=0 (4t)
1'	Y1=0.72 (6t)
1'	Y2=0.5 (12t)
1'	Y3=0.27 (6t)
1'	Y4=0.05 (4t)

Au pont 3

1'	Y0=0 (4t)
1'	Y1=0 (6t)
1'	Y2=0.5 (12t)
1'	Y3=0.27 (6t)
1'	Y4=0.05 (4t)

Page 52 sur 115

Au point 4

1'	0	=	0 (4	)
1'		=	0 (6	)
1'	2	=	0.5 (	2 )
1'	3	=	0.27	(6 )
1'	4	=	0.05	(4 )

Au point 5

1'	0	=	0 (4	)
1'		=	0 (6	)
1'	2	=	0.5 (	2 )
1'	3	=	0.27	(6 )
1'	4	=	0.05	(4 )

Au point 6

1'	0	=	0 (4 )
1'		=	0(6 )
1'	2	=	0( 2 )
1'	3	=	0.27 (6 )
1'	4	=	0.05 (4 )

Page 53 sur 115

Au point 7

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0.27 (6 )
1'	4	=	0.05 (4 )

Au point 8

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0 (6 )
1'	4	=	0.05 (4 )

Au point 9

1'	0	=	0 (4 )
1'		=	0 (6 )
1'	2	=	0 ( 2 )
1'	3	=	0 (6 )
1'	4	=	0.05 (4 )

Au point 10

1'	0	=	0	(4 )
1'		=	0	(6 )
1'	2	=	0	( 2 )
1'	3	=	0	(6 )
1'	4	=	0	(4 )

IV.1.3.4.2.1. Tableau récapitulatif des efforts tranchant

section	4t			6t			12t		somme	0.57M
	Y1	Y2	(Y1+Y2)4t	Y1	Y2	(Y1+Y2)6t	Y	12Y
0	0.94	0,05	3,96	0,72	0,27	5,94	0,5	6	15,9	9,063
1	0	0,05	0,2	0,72	0,27	5,94	0,5	6	12,14	12,14
2	0	0,05	0,2	0,72	0,27	5,94	0,5	6	12,14	12,14
3	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
4	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
5	0	0,05	0,2	0	0,27	1,62	0,5	6	7,82	7,82
6	0	0,05	0,2	0	0,27	1,62	0	0	1,82	1,82
7	0	0,05	0,2	0	0,27	1,62	0	0	1,82	1,82
8	0	0,05	0,2	0	0	0	0	0	0,2	0,2
9	0	0,05	0,2	0	0	0	0	0	0,2	0,2
10	0	0,05	0	0	0	0	0	0	0	0
somme			5,76			25,92		36	67,68	38,58

Page 54 sur 115

Page 55 sur 115

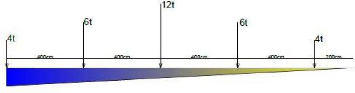
Cas 2 où le convoi se déplace sur le pont Au point 0

	0	=	(4	)
		=	0.77	(6	)
	2	=	0.55	(	2 )
	3	=	0.33	(6	)
	4	=	0.	(4	)

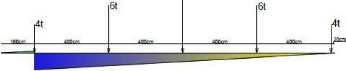
Au point 1

	0	= =	0.9 (4 ) 0.67 (6 )
	2	=	0.45	( 2 )
	3	=	0.23	(6 )
	4	=	0.0	(4 )

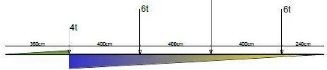
Au point 2

	0		=		0.8 (4 )
			=		0.57 (6 )
	2		=		0.35 ( 2 )

Page 56 sur 115

1'

	3	=	0.35	(6 )
1'	4	=	0. 3	(6 )

Au point 3

1'	0	=	0.7 (4 )
1'		=	0.47 (6 )
1'	2	=	0.25 ( 2 )
1'	3	=	0.033 (6 )
1'	4	=	0 (4 )

Au point 4

1' 1'	0	= =	0.6 (4 0.37 (6		) )
1'	2	=	0. 5	(	2 )
1'	3	=	0 (6	)
1'	4	=	0 (4	)

Au point 5

1'		0		=		0.5 (4 )
1'				=		0.27 (6 )
1'		2		=		0.05 ( 2 )

Page 57 sur 115

	3	=	0	(6 )
	4	=	0	(4 )

Au point 6

	0	=	0.4 (4 )
		=	0. 7 (6 )
	2	=	0 ( 2 )
	3	=	0 (6 )
	4	=	0 (4 )

Au point 7

	0	= =	0.3 (4 ) 0.07 (6 )
	2	=	0 ( 2 )
	3	=	0 (6 )
	4	=	0 (4 )

Au point 8

	Y0=0.2 (4t)
	Y1=0 (6t)
	Y2=0 (12t)
	Y3=0 (6t)
	Y4=0 (4t)

Page 58 sur 115

Au point 9

1' Y0=0.1 (4t) 1' Y1=0 (6t)

1' Y2=Y3=Y4=0

Au point 10

Nous avons pour valeur zéro dans tous les tronçons. IV.1.3.4.2.2.Tableau récapitulatif de l'effort tranchant

section	4t			6t			12t		somme	0.57M
	Y	Y	(Y +Y )4t	Y	Y	(Y +Y )6t	Y	12Y
0	1,00	0,11	4,44	0,77	0,33	6,60	0,55	6,60	17,64	10,05
1	0,90	0,01	3,65	0,67	0,23	5,40	0,45	5,40	14,45	8,24
2	0,80	0,00	3,20	0,57	0,13	4,20	0,35	4,20	11,60	6,61
3	0,70	0,00	2,80	0,47	0,03	3,02	0,25	3,00	8,82	5,03
4	0,60	0,00	2,40	0,37	0,00	1,48	0,15	1,80	5,68	3,24
5	0,50	0,00	2,00	0,27	0,00	1,08	0,05	0,60	3,68	2,10
6	0,40	0,00	1,60	0,17	0,00	0,68	0,00	0,00	2,28	1,30
7	0,30	0,00	1,20	0,07	0,00	0,28	0,00	0,00	1,48	0,84
8	0,20	0,00	0,80	0,00	0,00	0,00	0,00	0,00	0,80	0,46
9	0,10	0,00	0,40	0,00	0,00	0,00	0,00	0,00	0,40	0,23
10	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00	0,00

somme

22,74

38,09

21,60

22,49

66,83

Page 59 sur 115

IV.1.3.4.2.3. Tableau synthèse de trois cas

Section	CAS 1		CAS 2		A RETENIR
	T	T*crt	T	T*crt
0,00	15,90	9,06	17,64	10,05	10,05
1,00	12,14	6,92	14,44	8,23	8,23
2,00	12,14	6,92	11,60	6,61	6,92
3,00	7,82	4,46	8,82	5,03	5,03
4,00	7,82	4,46	5,68	3,24	4,46
5,00	7,82	4,46	3,68	2,10	4,46
6,00	1,82	1,04	2,28	1,30	1,30
7,00	1,82	1,04	1,48	0,84	1,04
8,00	0,20	0,11	0,80	0,46	0,46
9,00	0,20	0,11	0,40	0,23	0,23
10,00	0,00	0,00	0,00	0,00	0,00
SOMME		38,58		38,09	42,18

IV.1.3.4.2.4. Tableau des efforts tranchant dus au poids propre

Section	St		Pt ELS		Pt ELU		St*Pt ELS		St*Pt ELU
0	9		3,66		4,94		32,94		44,46
1	7,2		3,66		4,94		26,352		35,568
2	5,4		3,66		4,94		19,764		26,676
3	3,6		3,66		4,94		13,176		17,784
4	1,8		3,66		4,94		6,588		8,892
5	0		3,66		4,94		0		0

Page 60 sur 115

6

	-1,8	3,66	4,94	-6,588	-8,892
7	-3,6	3,66	4,94	-13,176	-17,784
8	-5,4	3,66	4,94	-19,764	-26,676
9	-7,2	3,66	4,94	-26,352	-35,568
10	-9	3,66	4,94	-32,94	-44,46

IV.1.3.4.2.5. Tableau des efforts tranchant dus à la foule

S-q-

ELU 0,00 0,02 0,06 0,14 0,24 0,38 0,55 0,75 0,98 1,24 1,53

section	S POS	S NEG	q POS ELS	q POS ELU	q NEG ELS	q NEG ELU	S+q+ ELS	S+q+ ELU	S-q-ELS
0	9	0	1,44	2,16	0,115	0,17	12,96	19,44	0,00
1	7,29	0,09	1,44	2,16	0,115	0,17	10,50	15,75	0,01
2	5,76	0,36	1,44	2,16	0,115	0,17	8,29	12,44	0,04
3	4,41	0,81	1,44	2,16	0,115	0,17	6,35	9,53	0,09
4	3,24	1,44	1,44	2,16	0,115	0,17	4,67	7,00	0,17
5	2,25	2,25	1,44	2,16	0,115	0,17	3,24	4,86	0,26
6	1,44	3,24	1,44	2,16	0,115	0,17	2,07	3,11	0,37
7	0,81	4,41	1,44	2,16	0,115	0,17	1,17	1,75	0,51
8	0,36	5,76	1,44	2,16	0,115	0,17	0,52	0,78	0,66
9	0,09	7,29	1,44	2,16	0,115	0,17	0,13	0,19	0,84
10	0	9	1,44	2,16	0,115	0,17	0,00	0,00	1,04

IV.1.3.4.3. Courbe enveloppe

Après avoir trouvé les moments fléchissant et les efforts tranchant dus au poids propre et aux surcharges fixes à la foule et au convoi, nous pouvons bien faire la sommation pour tracer la courbe enveloppe.

IV.1.3.4.3.1. valeurs des moments fléchissant

Section	POIDS PROPRE (1)		FOULE (2)		CONVOIS (3)		MOMENT (1)+(2)+(3)
	ELS	ELU	ELS	ELU	ELS	ELU	ELS	ELU
1,00	53,36	72,03	21,00	31,49	14,96	22,44	89,32	125,96
2,00	94,87	128,04	37,32	55,99	26,90	40,35	159,09	224,38
3,00	124,51	168,06	48,99	73,48	37,85	56,78	211,35	298,32
4,00	142,30	192,07	55,99	83,98	44,00	66,00	242,29	342,05
5,00	146,58	197,85	57,67	86,51	50,16	75,24	254,42	359,60

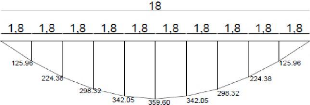
IV.1.3.4.3.1.1. Graphique de la courbe enveloppe du moment

IV.1.3.4.3.2. Valeurs des efforts tranchant

section	CONVOIS (1)		FOULE (2)				poids propre (3)		(1)+(2)+(3)
	ELS	ELU	T+ ELS	T- ELS	T+ ELU	T-ELU	ELS	ELU	ELS	ELU
0	10,05	15,08	12,96	0,00	19,44	0,00	32,94	44,46	55,95	78,98
1	8,23	12,35	10,50	0,01	15,75	0,02	26,35	35,57	45,09	63,67
2	6,92	10,38	8,29	0,04	12,44	0,06	19,76	26,68	35,02	49,56

Page 61 sur 115

3	5,03	7,55	6,35	0,09	9,53	0,14	13,18	17,78	24,65	34,99
4	4,46	6,69	4,67	0,17	7,00	0,24	6,59	8,89	15,88	22,83
5	4,46	6,69	3,24	0,26	4,86	0,38	0,00	0,00	7,96	11,93
6	1,30	1,95	2,07	0,37	3,11	0,55	-6,59	-8,89	-2,84	-3,28
7	1,04	1,56	1,17	0,51	1,75	0,75	-13,18	-17,78	- 10,46	- 13,72
8	0,46	0,69	0,52	0,66	0,78	0,98	-19,76	-26,68	- 18,12	- 24,23
9	0,23	0,35	0,13	0,84	0,19	1,24	-26,35	-35,57	- 25,15	- 33,79
10	0,00	0,00	0,00	1,04	0,00	1,53	-32,94	-44,46	- 31,91	- 42,93

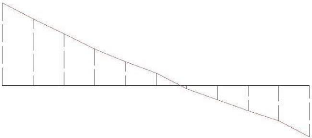
IV.1.3.4.3.2.1. Graphique de la courbe enveloppe de l'effort tranchant

Page 62 sur 115

Page 63 sur 115