Culture de bambou avec la fédération des associations caféières natives (facn) à Marmelade: motivations économiques et d?auto-subsistance et contribution au revenu global des exploitations agricoles

4.8.2- Tests statistiques

Pour confirmer ou infirmer la deuxième hypothèse de travail qui se base sur la comparaison des différents types d'exploitations agricoles sur la base de la contribution du bambou au revenu global, le test statistique qui a été retenu est celui développé par

28

B. L. Welch en 1947 (BAILLARGEON G. et RAINVILLE J., 1977). Ce test est ainsi présenté :

1. Hypothèses statistiques

H0 : u i = u j H1 : u i >-- u j ; i et j désignent les types à comparer¹⁸.

2. Hypothèses de base

Les hypothèses de base supposent un échantillonnage aléatoire de deux populations normales et indépendantes de variances inconnues et inégales et ni, n_j -.< 30.

3. Rapport critique et sa distribution

( X X

i - j

) - ( ì - ì )

t

=

Le rapport

i ^jdéveloppé par B. L. Welch en 1947 est distribué

s i

s_j

2 2

+

n_i

n_j

s j

( + )

s ²

i

2

2

n n

i j

approximativement suivant la loi de Student avec v = - 2

2

²

n i

s

( )

i

s

² ( )

j 2

+ n_j

degrés de

¹⁸Nous aurons à faire trois (3) comparaisons. En effet : le type 1 sera comparé avec les types 2 et 3, et ceux-ci seront comparés entre eux.

n i

+

1n + 1 j

liberté. V n'est pas nécessairement un nombre entier; nous prenons alors la valeur entière la plus rapprochée.

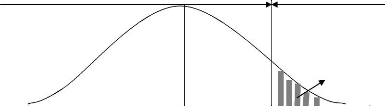
4. Région critique

Acceptation de H0 Rejet de H0

á = 0.05

t

0 tá; v

Figure 1: Région critique dans le test de Welch

29

5. Critère de décision

Rejeter H_o si _tcalcule >t a ; v ta;v est le t tabulaire.

4.8.3- Modèles économétriques

Pour effectuer les analyses de dépendance entre la variable endogène ou dépendante (quantité de bambous plantée) et les régresseurs ou variables exogènes ou indépendantes ou explicatives ou prédéterminées (taux d'autoconsommation des cultures autres que le bambou, revenu non agricole, revenu procuré par le bambou à la période précédente (année 2005)) citées dans l'hypothèse 1, le modèle économétrique qui a été construit est la régression linéaire multiple. Ce modèle s'écrit mathématiquement de la manière suivante : Q = a + a Z + a Z + a Z + p . Dans ce modèle, nous testons la

i 0 1 1 i 2 2 i 3 3 i i

part de la variabilité de Q expliquée par les Z_k et nous vérifions le respect des

conventions de la spécification en vérifiant les hypothèses d'adéquation d'usage suivantes :

H₁ : Les variables exogènes Z sont mesurées sans erreur et ont chacune une moyenne et une variance finie.

H₂ : Absence de biais systématique ; en d'autres termes, chaque perturbation p_j a une espérance mathématique nulle quelle que soit la valeur de Z_j.

H 3 : Homoscédasticité des erreurs, c'est-à-dire la variance de chaque p_j est la même "j E {1, 2, 3} et est indépendante de Z_j: var(Q_i) = var(p_i) = s .

2

H 4 : Les écarts résiduels suivent une distribution normale.

H 5 : Absence de colinéarité de l'ensemble des variables explicatives. 4.8.3.1- Spécification du modèle

Q = a + a Z + a Z + a Z + p ;

i 0 1 1 i 2 2 i 3 3 i i

Q : Quantité de bambous plantée (nombre de boutures mis en terre);

a₀: Niveau moyen de Q quand chaque variable explicative est nulle;

a_j : Accroissement de Q_j relatif aux variations de Z_j ; j = {1, 2, 3};

Z₁: Taux d'auto-consommation des cultures exprimé en valeur absolue (par rapport à 1);

30

Z₂ : Revenu non agricole exprimé en gourdes;

Z₃ : Revenu procuré par le bambou à la période précédente (année 2005) exprimé en

gourdes;

ì : Perturbations aléatoires.

4.8.3.2- Interprétation des á_j

Le grand mérite de l'analyse de la régression multiple, sa véritable raison d'être, est qu'elle permet d'isoler les effets respectifs des différents facteurs explicatifs, précisément lorsque les nombreuses variables qui interviennent n'ont pas été (et ne peuvent sans doute pas être) contrôlées expérimentalement. En tant qu'estimation des pentes ce sont les á _j (appelés coefficients de régression partielle) qui contiennent cette

information. Chacun représente l'estimation par les moindres carrés

de	? ? ??	? E ( Q Z 1 ,..., Z ) k	1 ? ??	, dérivée partielle de l'espérance conditionnelle^19de Q par rapport
		? Z j

aux variations du niveau de Z_j . Donc les á_j nous permettent de convertir les variations ceteris paribus de chacune des variables explicatives en une variation attendue de la variable dépendante. Chaque fois que la eme

j variable explicative subit une variation,
nous prévoyons que ÄQ = á _j ÄZ _j .

4.8.3.3- Estimation des paramètres

Pour estimer les paramètres du modèle, la méthode des moindres carrés ordinaires (MCO) a été mise en oeuvre. Cette méthode consiste à rechercher les valeurs qui minimisent la somme des carrés des écarts entre les valeurs observées de Q et celles prévues par le modèle. Il s'agit donc de minimiser par rapport à á₀, á₁ , á₂ , á₃

l'expression S(á₀,á₁,á₂,á₃) e_i avec

= ? 2 e = Q - ( á + á + á + á )

0 1 1

Z

i i i 2 2

Z . Les

i 3 3

Z i

conditions de premier ordre de ce problème de minimisation s'écrivent :

19 Chaque fois qu'on cherche à estimer une variable (Q) en tant que fonction d'une autre variable (Z), on calcule la quantité statistique E(Q Z) : c'est-à-dire l'espérance conditionnelle Q, étant donné la valeur

de Z déterminée antérieurement. ?+8

E ( Q Z ) = qf ( q z ₀ ) dq

-8

31

äS =2??ei^äei^?=0 ? j? {0, 1, 2, ^3}.äá ? äá ? ? ? j j ä ei Sachant que e = Q - (á +á Z +á Z +á Z ) et que donc = -1 i i 0 1 1i 2 2i 3 3i ä á0

et ?j ?{1, 2, 3}

. Chacune des conditions de premier ordre (nullité des dérivées partielles

ä ei =

-Zji

j

ä_á

premières) nous livre une équation, en effet : j = 0 na0 +â1?Z1i +á2?Z2i +á3?Z3i = ?Qi 2 j = 1 á0?Z1i +á1?Z1i +á2?Z1iZ2i +á3?Z1iZ3i = ?Z1iQi 2 j= 2 á^à0?Z2i +á1?Z1iZ2i +á2?Z2i +á3?Z2iZ3i = ?Z2iQi j = 3 á0?Z3i Z1iZ3i +á^à2?Z2iZ3i +á3?Z3i =?Z3iQi

Soit Zj , la moyenne de la eme

j- variable. En divisant par n la première équation, nous obtenons : Q = áà₀ +áà₁Z1 +áà₂Z2 +áà₃Z3 ce qui prouve que la droite de régression des moindres carrés passe par le point moyen.

Nous aboutissons donc à un système d'équations linéaires liant á₀, á₁, á₂, á₃, équations qui sont appelées « équations normales ». D'après l'algèbre élémentaire, on sait que, si ces équations (qui sont de forme linéaire et non homogène) sont également indépendantes et compatibles, leur solution fournira des estimations uniques pour les 4 paramètres²⁰.

Pour savoir si tel est le cas, il suffit d'étudier la matrice des coefficients : si le déterminant de cette matrice n'est pas nul, alors le système admet une solution. Les estimations des coefficients pourront être déterminées en résolvant le système. Cela fait,

20 Comme le lecteur peut avoir oublié certaines notions mathématiques élémentaires, nous rappelons ici quelques points essentiels. Compatible signifie que les inconnues doivent pouvoir vérifier simultanément toutes les équations. Par exemple, une variable z ne pourrait être en même temps égale à z+1 et à z-1. Indépendant signifie qu'il n'est pas possible de calculer une équation particulière comme la somme

pondérée des deux autres. Enfin, non homogène signifie que les termes de gauche (ici,?Q , ? Z ₁ Q , ? Z₂Q , ? Z₃ Q) ne sont pas tous nuls.

32

nous pouvons calculer la valeur du résidu empirique e_i pour toutes les observations par la formule e_i = Q_i - (d₀ + _â1Z1i + _â2Z2i + â3Z3i) ? i . La réécriture matricielle du système

à

Z 1

ì₁

e₁

á₀

j

Q₁

.

et aà =

.

.

.

=

=

e

.

Q

à

Znj

ì_n

e_n

á₃

Q_n

1 ? ? ? ? J

.

1

?

?

?

? J

.

1

?

?

?

?

J

.

1

?

?

?

? J?

.

1

?

.

ì = ? ?

? . ?

? ?

J

?j ? {1 , 3} Z_j =

Complétons la liste de nos vecteurs par un vecteur particulier Z₀ dont les n composantes sont toutes égales à 1 (soit ? i Z_i0 = 1). Rien ne nous interdit non plus, en juxtaposant les quatre vecteurs Z₀, Z₁, Z₂ , Z₃ , de composer une matrice à n lignes et 4 colonnes (c'est-à-dire une matrice de type n × 4) que nous appellerons Z :

1 1

Z Z 11 12 Z Z 21 22

Z13 Z23

.

.

Z = [ Z₀ , Z₁, Z₂ , Z₃ ] =

. . .

. . .

Z n Z n Z n

1 2 3

. L'intérêt essentiel de ce système de

1

1

?

?

?

?

?

J?

notations est de nous permettre de réécrire de manières très économes ces choses pour lesquelles nous dépensions beaucoup d'encre.

Tout d'abord, alors que le modèle théorique devait s'écrire :
Q_i = á₀ + _á1Z1i + _á2Z2i + _á3Z3i +ì_i ?i nous pouvons exprimer la même chose par

Q = Zá + ì . De la même manière, alors que la formule du résidu calculé s'exprimait : e_i = Q_i - (d₀ + â₁4 + _â2Z2i + â3Z3i) nous pouvons à présent écrire cette relation :

e = Q - Záà .

Mais il y a mieux. Le système d'équations fixant la valeur des coefficients estimés peut être maintenant sur une seule ligne. Il s'exprime, en effet, sous forme matricielle

ZT Záà = Z^T Q où T

Z est la transposée de la matrice Z. On montre, en effet, sans

difficulté :

Z^TZ = et que

J

?

?

? Z

T ? ? 1 i

=

Z₂

?

33

1

?

?

?

? J

Q_i

Z Q

?

Z₃

i i

Q_i
Q_i
Q_i

?1

1

?

?

n Z

i

Z2i

Z3i

1

2

Z

i Zli Z1iz2i Z1iz3i

1

2

Z2i Z

iZ2i Z2i Z2iZ3i

2

?

Z

?

?

Z3i

Z1i

3i

3i

Z2iZ3i

Z

Cela nous permet d'écrire áà sous la forme â = (Z^T Z)-1 Z^T Q où ( ) -

Z^TZ n'est autre

1

que l'inverse de la matrice Z^T Z .