|
So mmaire
Introduction générale 1
Chapitre 1 : Introduction aux antennes à
réseaux réflecteurs 4
1 Propriétés des antennes à réseaux
réflecteurs 4
1.1 Généralités 4
1.2 Avantages et inconvénients 5
1.3 Principe de fonctionnement 6
2 Solutions de cellules déphaseuses en technologie
imprimée 7
2.1 Principe d'utilisation des patchs 7
2.2 Ajout des stubs 8
2.3 Utilisation de la technologie multicouche 8
2.4 Les nouvelles technologies 9
3 Les outils de simulation 10
3.1 Le logiciel HFSS 10
3.1.1 Généralités 10
3.1.2 Méthode des éléments finis 11
3.2 La FDTD 11
4 Conclusion 12
Chapitre 2 :Les approches de simulation et de
mesure 14
1 Introduction 14
2 Les approches développées 14
2.1 La technique Floquet 14
2.1.1 Principe 14
2.1.2 Floquet / HFSS 15
2.1.3 Floquet / FDTD 17
2.2 L'approche cellule isolée 18
2.3 L'approche cellule environnée 19
2.4 La technique guide d'onde 20
3 Conclusion 21
Chapitre 3 :Calcul des angles et du champ
incident 23
1 Introduction 23
2 Position du problème 23
2.1 Calcul des angles 24
2.1.1 Calcul de (è i
,ö i ) 24
2.1.1.1 Méthode géométrique : 25
2.1.1.2 Méthode par changement de repères : 25
2.1.2 Calcul de (è' i
,ö' i ) 27
2.1.2.1 Méthode géométrique 27
2.1.2.2 Méthode par changement de repères 28
2.2 Définition du vecteur champ électrique
incident 30
2.2.1 Représentation du champ incident en projection
32
3 Conclusion 33
Chapitre 4 :Simulation de cellules
déphaseuses en incidence quelconque 35
1 Introduction 35
2 Procédure de caractérisation des cellules
déphaseuses en terme de matrice de réflexion 36
2.1 La polarisation 36
2.2 Radiations surfaces et PML 36
2.3 Conditions périodiques 36
2.4 Plans de mesure 37
2.5 Procédure de calcul (post-traitement) 38
3 Résultats et Validation de la procédure 40
3.1 Simulation sur un plan de masse 40
3.2 Simulation de cellules tirées du réseau
réel 42
3.2.1 Cellule simple patch chargée par une fente 42
3.2.1.1 Incidence normale : 43
3.2.1.2 Incidence oblique : 47
3.2.2 Cellule double patch chargée par deux demi fentes
50
4 Conclusion 52
Conclusion générale et perspectives 53
Bibliographie 54
Annexe 56

Chapitre 1
Introduction aux antennes à réseaux
réflecteurs
Introduction aux antennes à réseaux
réflecteu rs
1 Propriétés des antennes à
réseaux réflecteurs
1.1 Généralités
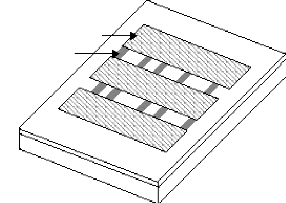
Une antenne réseau réflecteur est, comme son nom
l'indique, une combinaison entre le concept d'antennes réflecteurs et
celui d'antennes réseaux. Un réseau réflecteur est
constitué d'une source principale qui éclaire le réseau
imprimé. Ce dernier, dans sa forme la plus simple, n'est autre qu'un
réseau planaire de patch microstrip imprimé sur un substrat
plaqué sur un plan de masse (figure 1.1).

Figure. 1.1. Antenne réseau réflecteur
Le réseau est conçu pour que l'onde
réfléchie par chacun de ces éléments rayonnants
soit une onde plane, déphasée par rapport à la source
principale [Pozar97, Huang95]. De ce fait, ce réflecteur réseau
plan permet de contrôler et de rediriger en phase le re-rayonnement de la
source primaire dans la direction souhaitée (figure 1.2).
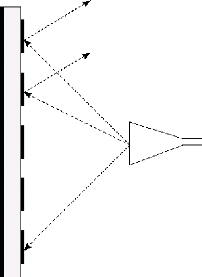
Figure. 1 .2.Principe de fonctionnement d'un réseau
réflecteur
Ainsi, l'utilisation des réseaux réflecteurs repose
sur la compacité (taille, poids), le coût de fabrication et la
possibilité d'avoir un faisceau orientable (reconfigurable).
1.2 Avantages et inconvénients
Les deux technologies utilisées dans la conception des
réseaux réflecteurs possèdent chacune leurs avantages et
inconvénients. Dans le cas des antennes réseaux, l'avantage
majeur est de pouvoir contrôler la pondération en amplitude et en
phase de chaque élément du réseau, et de permettre de
maîtriser la direction de l'onde émise et la forme du faisceau. En
plus, un contrôle électronique de chaque élément du
réseau autorise des vitesses de balayage très rapides.
L'inconvénient de cette technologie réside néanmoins dans
la complexité du circuit d'alimentation et dans les pertes induites.
Dans le cas des antennes à réflecteur, le problème du
réseau d'alimentation est résolu par l'utilisation d'une source
primaire unique illuminant le réflecteur. En contrepartie, il existe des
difficultés technologiques telles que le poids de l'antenne et le
dépointage mécanique de l'antenne [Girard03].
En outre, l'antenne réseau réflecteur combine les
avantages des deux technologies citées précédemment.
Ainsi, elle fonctionne avec une source primaire unique qui éclaire le
réflecteur plan (ce qui évite la mise en place d'un circuit
d'alimentation complexe et dissipatif). Etant donnés que, les
éléments rayonnants du réseau, appelés cellules
déphaseuses, re-rayonnent en phase l'énergie émise par la
source dans la direction souhaitée. Donc, les propriétés
de l'onde ré-émise seront commandées par la loi de phase
générée par le réseau. Cette loi de phase
correspond à la phase synthétisée par chaque cellule.
Ainsi, le re-rayonnement de l'onde émise peut subir des
dépointages importants sans jouer sur la position du réflecteur.
Cette loi peut également être utilisée pour
générer un diagramme de rayonnement de l'antenne
conformément à un gabarit donné. On peut noter que la
taille du réseau fixera la directivité maximale. Le pas du
réseau est choisi, quant à lui, en fonction des lobes de
réseau et du dépointage à affecter pour l'onde
ré-émise. Il reste après avoir pris en compte de ces
contraintes, imposées par les structures de l'antenne, à
définir la source primaire.
1.3 Principe de fonctionnement
Une antenne réseau réflecteur est donc
composée d'une source primaire qui illumine une surface
réflectrice contenant un réseau de cellules déphaseuses.
Ces cellules vont re-rayonner l'énergie provenant de la source. Cette
énergie totale ne sera pas re-rayonnée en phase si tous les
éléments constitutifs du réseau sont identiques. Ceci est
du au fait que pour une surface réflectrice plane, le champ qui se
propage de la source primaire vers les éléments rayonnants
effectue des trajets différents (figure 1.2). En effet, si chacune des
cellules constituant le réseau est capable de fournir une phase
ajustée pour compenser les différences du trajet, le champ total
re-rayonné aura une phase identique pour chaque cellule dans l'axe
(direction de l'axe perpendiculaire au réseau). Pour cela, pour couvrir
cette plage de compensation, la réponse en phase des cellules
déphaseuses doit dépendre d'un paramètre (la longueur de
patch, la longueur des stubs, l'épaisseur du substrat...). Ainsi, la loi
de phase est la capacité d'une cellule à pouvoir
générer une valeur de phase en fonction d'un paramètre
lié à la cellule.
Ce concept de compensation des phases a été
introduit depuis de nombreuses années avec l'utilisation
d'éléments rayonnants tels que des cornets, des dipôles, et
des guides d'onde [Huang91, Girard03, Huang96]. Mais, ces structures sont
encombrantes et lourdes. Cependant, l'utilisation des technologies
réseaux imprimés a permis la fabrication d'antenne réseau
réflecteur plus légère, moins encombrante et à
moindre coût. Depuis lors, de nombreuses études
portant sur le développement de cellules
déphaseuses imprimées ont été investiguées
[Girard03, Alex02]. Une méthode consiste à utiliser des patchs
microruban de la même dimension, chaque cellule pouvant être
chargée par un stub de longueur variable [Girard03]. D'autres solutions
ont été développées en jouant sur la dimension des
patchs [Chenakin97] ou en changeant l'épaisseur du substrat de
manière à contrôler le déphasage
[Encinar99,Encinar01]. Dans chacun de ces cas, le dimensionnement des cellules
est déterminant pour les performances.
2 Solutions de cellules déphaseuses en
technologie imprimée
Les solutions développées, dans notre laboratoire,
pour la réalisation des cellules déphaseuses sont principalement
basées sur l'utilisation de patchs résonnants.
2.1 Principe d'utilisation des patchs
En variant les dimensions de l'élément
rayonnant, nous pouvons contrôler le déphasage (figure 1.3).
Ainsi, pour une onde incidente sur le réseau de patch à taille
variable, la phase de l'onde réfléchie varie avec les dimensions
du patch. En effet, la variation des dimensions du patch suivant l'orientation
de la polarisation de l'onde incidente, oblige les courants induits sur ce
dernier à parcourir un chemin variable changeant ainsi la longueur
résonnante du patch.
patch
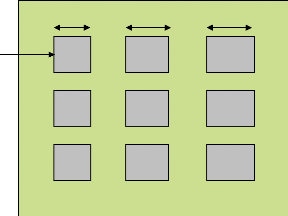
a1 a2>-a1
a3>-a2
Figure.1.3. Réseau de patchs à taille variable
Cette longueur de résonance est inversement liée
à la fréquence de résonance du patch. Donc, la variation
de cette fréquence de résonance conduit à la variation de
la phase re-rayonnée par le patch. Cette phase dépend alors du
chemin parcouru sur le patch.
2.2 Ajout des stubs
Parmi les solutions envisagées pour la
réalisation de cellules déphaseuses, nous pouvons décrire
celle qui consiste à ajouter un tronçon de ligne à
l'élément résonnant [Chenakin97]. Ainsi, le contrôle
du déphasage s'effectue par la variation de la longueur du stub (figure
1.4).
stubs
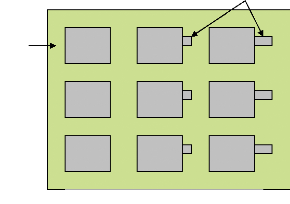
Figure. 1.4. Réseau de patchs et stubs
patch
Cette technique est limitée en bande de fréquence,
due à la faible bande du stub, et présente un encombrement sur la
maille des cellules.
2.3 Utilisation de la technologie multicouche
C'est une méthode qui consiste à avoir un
réseau multicouche de patchs de différentes tailles [Encinar01,
Agustin03]. Elle permet de couvrir une gamme importante (supérieure
à 360°). Sur chaque couche de substrat est gravé un
réseau de patchs et donc, dans chaque maille du réseau plusieurs
cellules déphaseuses positionnées les unes en dessous des autres
(figure 1.5). Le principe de cette méthode consiste à
séparer les fréquences de résonance de chaque cellule et
les faire résonner les unes après les autres ce qui permet
d'avoir des gammes de phases supérieures à 700°.
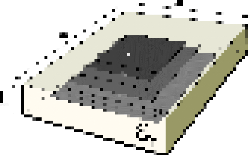
Figure. 1.5 Patch multicouche
Néanmoins, les technologies multicouches utilisées
restent difficiles à mettre en oeuvre et le coût de fabrication
est relativement élevé.
2.4 Les nouvelles technologies
Les solutions citées précédemment
fournissent des lois de phase fixes. Actuellement, on s'oriente vers des
solutions re-configurables. C'est en pilotant les phases de chacun des
éléments du réseau de manière indépendante
qu'on obtient des réseaux réflecteurs re-configurables. Ainsi le
faisceau de l'antenne n'est plus fixe mais orientable. Pour ce faire, les
techniques passives de déphasage citées
précédemment sont transposables moyennant l'introduction
d'éléments actifs (figure 1.6) tels que : diodes [Agustin03],
varactors [Agustin03], MEMS [Girard03]...).
MEM S micocommutateur
Figure. 1 .6.Cellule déphaseuse active avec MEMS
Des études précédentes menées par
divers projets en collaboration avec la société Alcatel Space,
l'Agence Spatiale Européenne et bien évidemment notre laboratoire
IETR, ont montré la nécessité d'outils de simulation pour
le dimensionnement des réseaux réflecteurs
(caractérisation des cellules déphaseuses). De ce fait, nous
distinguons pas mal d'outils de simulation, en particulier, le logiciel
commercial HFSS (High Frequency Structure Simulation) d'Ansoft et un code
basé sur la méthode des Différences
Finies dans le Domaine
Temporel (FDTD) développé au sein de notre
laboratoire IETR.
3 Les outils de simulation
3.1 Le logiciel HFSS
3.1.1 Généralités
H.F.S.S est un simulateur électromagnétique de
haute performance pour les modèles en 3D. Il intègre des
simulations, des visualisations et une interface automatisée facile
à utiliser pour résoudre rapidement et de façon efficace
les problèmes électromagnétiques en 3D. Son code de calcul
est basé sur la méthode des éléments finis
(méthode fréquentielle), des graphiques performants pour donner
à l'utilisateur des résultats et une perspicacité aux
problèmes électromagnétiques en 3D.
Une croissance H.F.S.S peut être utilisée pour
calculer des paramètres tels que les paramètres S, les
fréquences de résonance et les champs. C'est un outil permettant
le calcul du comportement électromagnétique d'une structure. Le
simulateur possède des outils de post traitement pour une analyse plus
détaillée. Il permet le calcul des :
· Quantités de base : champ proche, champ
lointain
· Impédances caractéristiques des ports et
leurs constantes de propagation
· Les paramètres S normalisés par rapport
à une impédance de port spécifique Afin de
générer une solution du champ électromagnétique,
H.F.S.S emploi la méthode des éléments finis. En
général, cette méthode divise l'espace de
résolution du problème en plusieurs milliers de régions
plus petites et représente le champ dans chaque sous région
(élément) avec une fonction locale.
3.1.2 Méthode des éléments
finis
La géométrie du modèle,
étudié sous H.F.S.S, est automatiquement divisée en un
grand nombre de tétraèdres. La valeur d'un vecteur champ (E ou H)
en un point à l'intérieur d'un tétraèdre est
calculée par interpolation des valeurs des champs dans les sommets du
tétraèdre. Ainsi, en représentant les valeurs des champs
de cette manière, H.F.S.S transforme les équations de Maxwell en
équations matricielles qui sont résolues par les méthodes
numériques classiques. En divisant la structure en plusieurs petites
régions, H.F. S. S calcule les champs séparément dans
chaque élément en fixant des critères de convergence. Plus
les éléments sont petits, plus la solution est précise
mais plus le temps de calcul est long.
3.2 La FDTD
C'est une méthode basée sur la résolution
des équations de Maxwell. Ces équations sont conçues pour
décrire la création et la propagation d'une onde
électromagnétique dans un milieu bien déterminé. La
méthode des différences finies temporelles est fondée sur
le schéma explicite de Yee []. Elle permet de calculer à chaque
instant discret de l'espace, les composantes du champ
électromagnétique dans chaque cellule
parallélépipédique du volume tridimensionnel (figure
1.7).
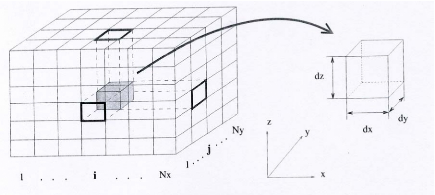
Figure. 1.7. cellule parallélépipédique
Les composantes des champs électromagnétiques sont
représentées à la figure 1.8.
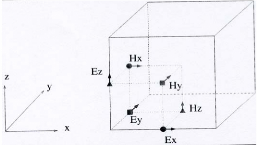
Figure. 1.8. Disposition des champs
électromagnétiques
Des conditions aux limites doivent être définies
autours du volume de simulation pour le calcul des champs
électromagnétiques. Cette méthode est une méthode
de calcul volumique et donc en particulier bien adaptée à
l'étude des cellules imprimées sur des substrats. Son avantage
est la résolution 3D même de structures complexes [Taflove00].
Mais, elle nécessite de mailler tout le volume défini, ce qui
peut devenir rapidement prohibitif en terme de temps de calcul et de
matériel informatique à mettre en oeuvre. Enfin, c'est une
méthode temporelle qui permet de caractériser des structures sur
une large bande de fréquence en une seule simulation (annexe A),
[Taflove98, Taflove95].
4 Conclusion
Au cours de ce chapitre, nous avons présenté une
synthèse sur les propriétés des antennes à
réseau réflecteur tout en donnant les avantages et les
inconvénients qui découlent de leurs utilisations ainsi que les
différentes techniques utilisées pour la réalisation des
cellules déphaseuses. Ensuite, une présentation des fondements
théoriques des outils de simulation utilisés a été
élaborée. Pour cela, une idée assez complète sur
les approches développées au sein de notre laboratoire pour les
études des cellules déphaseuses sera développée
dans le chapitre suivant.

Les approches de simulation et de mesure
Chapitre 2
Les approches de simulation et de
mesure
1 Introduction
Trois techniques ont été mises au point, dans notre
laboratoire, utilisant HFSS et/ou FDTD. On peut distinguer :
v' Utilisation de parois périodiques de Floquet (HFSS et
FDTD)
v' Utilisation de l'approche dite `cellule isolée'.
v' Utilisation de l'approche dite `cellule environnée'.
De plus, une quatrième technique utilisant un guide d'onde
a est développée pour les mesures.
2 Les approches développées
Dans cette partie, nous essayons de présenter les
différentes approches développées pour l'études des
cellules déphaseuses au cours des travaux de recherche effectués
dans notre équipe.
2.1 La technique Floquet
2.1.1 Principe
Cette méthode est développée par le
mathématicien G. Floquet [Floquet1 879] afin de définir des
solutions périodiques pour ces équations différentielles.
Dans le cas général d'un volume éclairé par une
onde incidente plane, les conditions de Floquet s'expriment ainsi : le champ
incident en B est identique au champ incident en A affecté d'un
décalage temporel correspondant à la différence de chemin
entre A et B (figure 2.1).
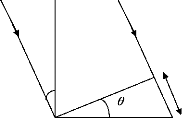
è
A
?
B
Figure.2. 1. Volume éclairé par une onde en
incidence quelconque
La différence de chemin est ainsi ? =
AB.sin(è) et donc le décalage temporel
associé est sin().AB
dt
Où v est la vitesse de l'onde.
è
v
øB(xB,yB,zB,t)=øA
( x A,yA, z
A, t - dt ) Eq.2.1
øA(xA,yA,zA,t)=øB
( x B,yB, z
B, t + dt ) Eq.2.2
La difficulté d'exploitation des conditions de Floquet
dans le cas général d'une onde en incidence quelconque ne
provient pas du fait qu'il faille, (Eq.2.1), exprimer le champ en B en fonction
du champ en A affecté d'un retard dt. Cela se traite en stockant les
valeurs calculées du champ en A. Le calcul du champ en A à
l'instant t en fonction du champ en B, (Eq.2.2), par contre fait intervenir le
champ en B mais à un instant précédent l'instant t,
instant que l'on ne peut connaître lors du calcul à t
[Girard03]
Nous remarquons, bien évidemment, qu'en incidence normale,
les conditions de Floquet se simplifient énormément.
Cette méthode vise à simuler un réseau
infini de cellules toutes identiques à partir de la simulation d'une
seule cellule (voir figure 2.2).
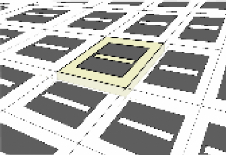
Figure.2.2. Simulation de réseau infini de cellules
2.1.2 Floquet / HFSS
Le logiciel HFSS, déjà présenté,
nous donne la possibilité d'étudier des cellules
déphaseuses. En effet, l'idée se base sur le fait de
définir des `parois de Floquet' autour de la cellule sous test pour
créer artificiellement le comportement d'un réseau infini dont
toutes les cellules sont identiques, ce qui permet d'étudier l'effet de
couplage entre les cellules voisines. Pour ce faire, nous avons crée une
boite à six faces où on met la cellule sous test (figure 2.3).
Les quatre faces entourant la cellule sont définies comme des parois
périodiques (de Floquet) et la face supérieure comme une surface
d'excitation pour appliquer le champ incident. La dernière
face est celle appliquée sous le substrat, correspond
au plan de masse. Pendant [CadoretF05, CadoretM05], le champ rayonné
évalué est celui en champ lointain. Il est calculé en
utilisant une sphère infinie définie à l'aide du logiciel
et donc on peut récupérer la phase du champ lointain de
façon spéculaire et donc de définir la réponse en
phase de la structure sous test.
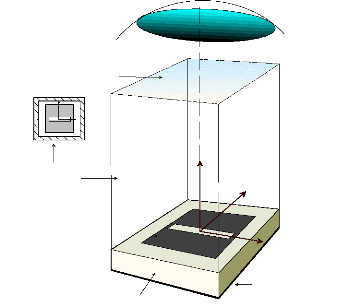
sphére infinie
surface d'excitation
y
x
conditions périodiques de floquet
cellule sous test
z
y
x
plan de masse
substrat
Figure.2.3. Utilisation de parois de Floquet sous HFSS
L'avantage majeur du logiciel HFSS est la rapidité des
calculs effectués et la facilité de son utilisation. De plus,
c'est une technique qui nous permet de faire des études
paramétriques. Ainsi, c'est une approche performante à exploiter
pour fournir des bases de données et elle peut être
généralisée dans le cas d'une incidence quelconque qui
sera le but de notre travail. Néanmoins, cette méthode
possède pas mal de limitations dues à l'utilisation des
conditions périodiques. En effet, le réseau simulé est un
réseau infini périodique de cellules toutes identiques. Or, en
réalité, chaque cellule est entourée de voisines aux
dimensions différentes et donc on ne prend pas en compte
réellement des effets de couplage. De plus, les résultats en
phase ne sont pas réellement exploitables en dehors de la direction
spéculaire de rayonnement.
2.1.3 Floquet / FDTD
Comme nous venons de le voir au premier chapitre, la
méthode F.D.T.D est basée sur la résolution des
équations de Maxwell. Un code FDTD doit être
développé pour la définition du volume de calcul et pour
prendre en compte des conditions absorbantes ou dans notre cas les conditions
périodiques de Floquet. Cette méthode reprend la même
façon de définir les parois entourant la cellule sous test
(parois de Floquet) et la paroi d'excitation au dessus de la cellule
(figure2.4) En plus, une surface placée au dessus de celle d'excitation
est dite surface de Huygens car nous appliquons sur cette surface le principe
d'équivalence de Huygens [Alex02]. En d'autres termes, le volume F.D.T.D
délimité la surface de Huygens, dans lequel nous retrouvons les
vecteurs de champs et de courants électriques et magnétiques dus
au rayonnement de la source, est équivalent à la surface de
Huygens, où sont définis des courants magnétiques et
électriques équivalents.
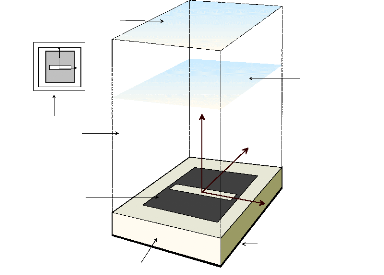
surface de Huygens
Surface d'excitation
z
conditions périodiques de floquet
cellule sous test
y
x
plan de masse
substrat
y
x
Figure.2.4 Utilisation de parois de Floquet (méthode
FDTD)
C'est à partir de ces courants que nous
déduisons les potentiels vecteurs pour le calcul des champs. Ainsi, la
méthode temporelle du calcul F.D.T.D permet des études en
fréquence et ce code développé dans notre laboratoire nous
permet de prendre en compte de parois de Floquet
mais ce code F.D.T.D reste ergonomique et la définition du
maillage de structures compliquées laborieuse.
2.2 L'approche cellule isolée
Pour observer le re-rayonnement d'une cellule sous une
incidence quelconque, nous avons choisi de la simuler à l'aide de la
méthode FDTD puisque, avec l'utilisation des parois de Floquet sous
HFSS, nous ne pouvons pas chercher les résultats de re-rayonnement en
dehors de la réflexion spéculaire. Néanmoins, ce choix
introduit une hypothèse simplificatrice qui consiste à ne pas
considérer les effets de couplage. La figure 2.5 montre que la paroi
d'excitation entoure toute la cellule sous test. Cette surface d'excitation
génère une onde plane en incidence quelconque.
surface d'excitation
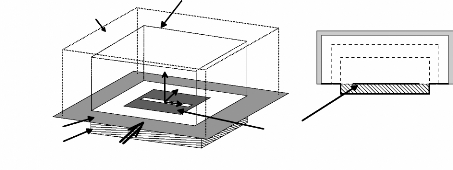
surface d'Huygens
surface d'Huygens surface d'excitation
z
y
z0x plane
x
plan de masse cellulaire unitaire
substrat
polarisation de l'onde incidente
PMLs
Figure.2.5 Méthode de simulation FDTD d'une cellule
unitaire
Le champ total re-rayonné est
récupéré en champ proche à l'aide de la surface de
Huygens définie et le champ lointain dans toutes les directions est
alors déduit de ces résultats en champ proche
[Cadoret04,CadoretM05,Milon06]. Ceci permet d'accéder au diagramme de
rayonnement de la cellule isolée sous incidence quelconque et donc
à caractériser son fonctionnement. Ainsi, cette méthode
permet de fournir une base de données, un temps de simulation
réduit ainsi qu'un calcul du rayonnement dans n'importe quelle direction
et sous n'importe quelle incidence. Toutefois, cette méthode
néglige l'effet de couplage puisque seule la cellule est
étudiée.
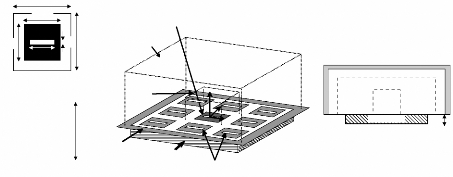
2.3 L'approche cellule environnée
Nous venons de voir que la méthode `cellule
isolée' a négligé l'effet de couplage. Pour cela, dans le
cadre de travail de thèse effectué par M-A Milon, une autre
méthode d'analyse est développée. Celle-ci consiste
à éclairer une seule cellule du réseau et à
considérer son rerayonnement en présence de ses voisines
immédiates (identiques ou non) [Milon06]. Cette méthode permet
donc de calculer le re-rayonnement d'une cellule environnée dans
n'importe quelle direction et sous n'importe quelle incidence et surtout dans
un environnement réaliste. Cette méthode, incluant plus
d'éléments, nécessite un volume d'étude plus
important et donc un temps de calcul plus important. En effet, seule la cellule
centrale est illuminée par une onde plane d'incidence . La phase de
l'onde re-rayonnée est alors calculée en prenant en compte la
(? i ,ij i )
contribution des huit cellules voisines les plus proches. Pour
cela, deux surfaces sont définies dans le volume de calcul FDTD (figure
2.6). La surface d'excitation entoure la cellule centrale et délimite le
volume dans lequel le champ incident est appliqué. La surface de
Huygens, quant à elle, qui est utilisée pour calculer le champ
re-rayonné, inclus les neuf cellules et vient se renfermer sur le plan
de masse.
a
b
cellule centarle éclairée par l'onde
incidente
a surface de Huygens
xpatch?
ypatch
b
PMLs
structure simple patch
surface d?excitation
z
surface de Huygens surface d?excitation
y
h
x
substrat
zox plan
plan de masse
polarisation de l?onde incidente
cellules voisines à la cellule centarle
Figure.2.6. Méthode de simulation FDTD d'une cellule
environnée
Ainsi, cette méthode permet d'évaluer le
couplage mutuel entre les cellules voisines, une prédiction des
diagrammes de rayonnement dans un environnement réel et une simulation
de réseau contenant des cellules différentes. C'est une technique
plus réaliste pour l'étude d'un réseau réflecteur
mais elle demande un temps de calcul plus important ainsi qu'un matériel
informatique assez puissant.
2.4 La technique guide d'onde
C'est une méthode basée sur le principe
d'utiliser un guide d'onde à la fréquence de fonctionnement
désirée et d'effectuer des mesures pour le coefficient de
réflexion de chaque cellule (amplitude et phase du champ
réfléchi). Pour cela, on réalise plusieurs cellules dont
les dimensions sont différentes, nous les positionnons ensuite au fond
du guide alternativement en mesurant à chaque fois la réponse en
phase et en amplitude de chaque coefficient de réflexion (figure
2.7).

Figure.2.7. Guide d'onde et cellules déphaseuses
positionnées
Nous traçons alors la loi de phase correspondante pour
la variation d'un paramètre de la cellule. Ainsi, c'est une mesure d'une
seule cellule dans un environnement sans interaction de cellules voisines (sans
effet de couplage). De ce fait, cette technique nous permet de valider les
principes de structures adoptées pour l'étude des cellules
déphaseuses et nous fourni une idée sur les pertes.
Néanmoins, chaque fois, nous étions amenés à
réaliser un nombre important de cellules.
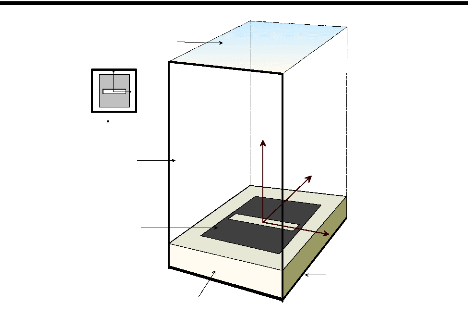
A titre indicatif, que nous pouvons comparer les mesures avec
des simulations effectuées sous HFSS en remplaçant les parois de
Floquet par des murs électriques (pour avoir un environnement de guide,
figure 2.8)
port d'excitation
y
x
z
conditions périodiques de floquet
cellule sous test
y
x
plan de massse
substrat
Figure.2.8. Utilisation de murs électriques
De cette manière, nous pouvons donc comparer entre
simulation et me sure pour valider le principe des cellules
déphaseuses.
3 Conclusion
Dans le cadre général de notre travail sur la
description des différentes procédures de caractérisations
des cellules déphaseuses, nous venons de présenter les
différentes méthodes développées dans notre
laboratoire. De plus, en réalité, la réponse en phase de
chaque cellule dépend des paramètres de dimensionnement de cette
dernière mais à ceux-ci s'ajoutent les paramètres
d'illumination. De ce fait, nous nous intéressons au cours du
troisième chapitre à définir les caractéristiques
d'éclairement d'une cellule du réseau en tenant compte le
rayonnement du cornet.

Calcul des angles et du champ incident
Chapitre 3
| 


