Etude de cellules rayonnantes pour réseau réflecteur

Calcul des angles et du champ incident

1 Introduction

Un réseau réflecteur est composé, comme nous avons vu précédemment, de cellules déphaseuses illuminées par une source primaire. Ces dernières sont positionnées sur une surface réflectrice. Les différences de trajet, de la source à la surface réflectrice, vont être compensées en phase par chaque cellule du réseau. Cette phase doit être dépendante de la position de chaque cellule dans le réseau. En réalité, la réponse en phase de chaque cellule dépend des paramètres de dimensionnement de cette dernière mais à ceux-ci s'ajoutent les paramètres d'illumination. En effet, la cellule déphaseuse est vue sous un angle d'incidence et une polarisation différents qui dépendent bien évidemment de la position de cette cellule dans le réseau (annexe B).

Ainsi, au cours de notre travail, nous avons pensé à améliorer nos simulations en tenant compte du rayonnement du cornet pour s'approcher d'un cas réel d'étude de réseau réflecteur. Pour cela, nous avons besoin de définir les caractéristiques d'éclairement d'une cellule du réseau. En effet, nous nous plaçons dans le cadre, par exemple, de notre travail effectué lors de ce stage (simulation à l'aide du logiciel HFSS). La cellule (notée cellule i) est supposée éclairée par une onde plane dont il faut préciser l'incidence et la polarisation. Ces grandeurs sont définies à partir de la configuration réelle du réseau. Pour l'incidence, nous définissons ainsi les angles (O _i , çt _i )

précisant la direction sous laquelle est vu le cornet dans le système de coordonnées sphériques associé à la cellule i. Pour la polarisation, nous supposons que le cornet rayonne en co-polarisation (au sens de Ludwig 3) [Ludwig73, Hansen87]. Par conséquent, la définition de la polarisation nécessite de travailler dans la base liée au cornet. Il faut donc définir d'abord la polarisation dans la base liée au cornet avant de la transposer dans la base du réseau (où la simulation de la cellule sera faite). Ce changement de base demande entre autres de définir la direction sous laquelle est vue la cellule i dans le système de coordonnées sphériques

(O'_i,çt'_i)

attaché au cornet.

2 Position du problème

En réalité, un réseau est composé d'un nombre important de cellules. Dans notre étude, nous nous intéressons à un cas de réseau de 437 cellules pour une maille de 0.7 ) 0 = 16.8 mm,

fonctionnant à une fréquence de 12.5 GHz. Chaque cellule possède des dimensions propres à son emplacement dans le réseau et contribue différemment en phase et en amplitude au diagramme de rayonnement du réseau complet. (annexe B)

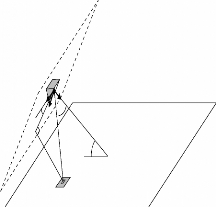
Nous commençons par définir la configuration générale, en perspective, d'un réseau réflecteur et les différents paramètres pris en compte pour pouvoir calculer ses angles.

Le point O est le centre du réseau. Le point O' est le centre de phase du cornet. Le point Oi représente le centre de la i^ème cellule du réseau. Le système de coordonnées ( est

O, x, y, z)

attaché au réseau et le système de coordonnées est attaché au cornet. On note á

(O',x',y',z')

l'angle d'élévation du cornet, H sa hauteur par rapport au plan du réseau et (x _c ,y _c ,z _c )les coordonnées du cornet. (figure 3.1)

O'

x'=x z'
y'

H z

Oi x_i y_i x O y

Figure.3. 1 Configuration générale d'un réseau réflecteur

2.1 Calcul des angles

Pour accomplir notre calcul des angles déjà mentionnés, nous avons développé deux méthodes afin de confirmer et de valider nos calculs ainsi fournis. En effet, nous avons élaboré deux méthodes intitulées : méthode géométrique (basée sur un raisonnement géométrique) et méthode par changement de repères (utilisation des relations entre les coordonnées sphériques et cartésiennes).

2.1.1 Calcul de (èi,ö _i )

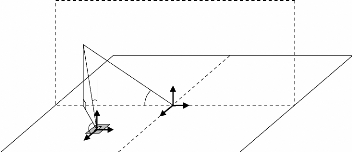
Les angles définis sent la direction sous laquelle est vu le cornet dans le système de

(? i , ç, _i )

coordonnées sphériques associé à la cellule i :

H

di

O'

ö_i

x

li

è_i

O_i

z

y

l0

á

x

O

z

y

Figure.3.2 Définition des angles (? i , ij _i )

Avec H : projeté orthogonal de O' sur le plan (x, y) l₀ : Distance cornet- cellule centrale

l_i : Distance cornet- cellule i

2.1.1.1 Méthode géométrique :

Dans le triangle rectangle O 'HO_i , on peut écrire :

tg() i

è= avec d_i = x i 2 + (y _i - y c 2

d ) d'où on en déduit :

i H

è_i

)

= arctg

H

yyc i
-

De même, on peut voir que :

ð x

ö = + â avec () i

tgâ=

i 2

ce qui nous permet d'écrire :

ð

ö = + arctg(

i 2

)

x_i

yy^- c i

Eq3.1

Eq3 .2

2.1.1.2 Méthode par changement de repères :

Les coordonnées du centre de la cellule i (point Oi) dans le repère lié au centre du réseau (point O) se déduisent de:

OO _i = x _i e^G_x + y _i e^G_y

Les coordonnées cartésiennes du cornet (point O') dans le repère lié au centre du réseau (point O) se déduisent de :

OO' = -H tanáeG _y + HeG _z

Dès lors, les coordonnées de O' dans le repère lié au centre de la cellule i vérifient :

'

- x_i

O_iO'= O _i O+OO C'est-à-dire :

' ' '	? ? ? ? ?		-
á		? ? ? ??			(1)

x i

-

y_i

H tan

H

O

y i

O

z i

O

Les angles(è _i ,ö _i ), définissant la direction sous laquelle est vu le cornet dans le système

de coordonnées sphériques associé à la cellule i, se déduisent des relations entre coordonnées cartésiennes et sphériques :

? ??

??

y = r sin

è

cos

xr
=

zr
=

sin

èö

cos

Eq3.3

è ö

sin

On obtient ainsi:

tanö	y i O = i i xO

z_O '

' '

ö i Eq3.4

xyⁱ i
'' cossin ö+
O i O

^??i

?

tanè _i i

Donc (Eq3.3 Eq3.4) et (1) donnent	tg	() öi	y+ i	H ( ) tg() á

D'où

x i

Ainsi :

H

( )

tg( )

á

ö = )

i

y+

i

arctg(

x i

Eq3.5

Eq3 .6

? ?

H

( ) ( )

H

^{ö ö}

+ ? + ? ⁱ()

De même,

tg() è=

i

? ?

H

xy.cos()().sin() öö i i i i
+ ? ? +??
tg() á

è = -

arctg( )

i H

et donc

Eq3.7

Les relations (Eq3.1), (Eq3.2), (Eq3.5) et (Eq3.6) définissent donc à partir des paramètres

(O _i ,ij _i )

géométriques du réseau. Ces angles sont utilisés dans la simulation d'une cellule élémentaire pour définir l'angle d'incidence.

2.1.2 Calcul de (è' _i ,ö' _i )

La même démarche s'applique pour angles précisant la direction sous laquelle est vue la
(Oç,ijç)

cellule i dans le repère lié au cornet.

2.1.2.1 Méthode géométrique

Les angles définissent la direction sous laquelle est vue la cellule i dans le système de

(O'i,ij' _i )

coordonnées sphériques attaché au cornet (figure.3.4).

ö'_i

x' z'

y'

H

O'

O_i

è'_i

á

Fig.3.3 Définition des angles (O' _i ,ij' _i )

Dans le triangle quelconque OO'Oi, on a la relation suivante :

D^² = l i ²+l0²-2.l0.l i .cos(è ' i )

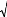
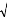
Avec 22

D=x _i +y _i et 2 2

li= ( x c - x i ) + ( y c - y i ) + z c 2

D'où 0

è + -

= ²

l l D

i ² ²

cos(')

i 2..

ll

0 i

llD
+ -

è)

_i^² ² ²

0

'os(

=arc

i 2..

l l

0 i

Nous notons la difficulté rencontrée pour la détermination de l'angle ö'_i par la méthode géométrique.

2.1.2.2 Méthode par changement de repères

Nous commençons par calculer les coordonnées cartésiennes de Oi dans le repère . Ensuite, nous utilisons les relations entre coordonnées cartésiennes et
(O', x ', y', z')

sphériques comme précédemment.

Les coordonnées de O dans le repère lié au cornet sont données par:

O O _G

H

' e_z

sin

=

'

á

Dès lors, les coordonnées de Oi dans le repère lié au cornet résultent de :

O'O_i =O'O+OO _i

H

Soit :OO= G + G +

' i e z x _i e _x y _i e y

'

sin á

H_{G G G}

O O

' = _á+ + -

' _'(cos_'sin '

i z i x i z y

e xeye e

áá)

sin

D'où :

x_i

H₊

y_i

sin

á

y_i cos

'

^xO_i

'

^yO_i

'

^zO_i

? ? ?

? ?

-

sin

á

? ? ? ? ?

á

(2)

? ?

Après avoir déterminé les coordonnées cartésiennes, les coordonnées sphériques se

déduisent d'une façon analogue que les angles , nous aurons alors d'après l'équation

H

+ y_i

sin()

á

(? i ,ij _i )

Eq3 .8

(Eq3.12): tg ö= (') i	-	á y.sin() i D 'où
			i
		xi

y.sin()

á

arctg_x)

i

ö=- '(ⁱ

Ce qui nous amène à écrire :

Eq3.9

.cos(') .sin().sin(')

öáö_i

i i

- y

.cos()

á

è ' (

= arctg

i

)

x_i

H

+

y_i

sin()

á

IETR 28

De même, on a : .cos(').sin().sin(')

xy

i i i

öáö_i

-

tg(') è=

i

.cos()

á

Les relations (Eq3 .7), (Eq3 .8) et (Eq3 .9) définis sent donc à partir des paramètres

(0' _i , q ' i )

géométriques du réseau. Ces angles déterminent l'orientation du champ électrique incident.

En second lieu, nous avons implanté un programme sous le logiciel Matlab (annexe C) pour nous fournir les angles voulus pour différentes positions du cornet (différentes configurations de réseau) tout en validant par quelques cas canoniques (incidence normale, cellules situées dans le

plan vertical passant par le cornet). De ce fait, la détermination de l'angle est directe pour le

q_i

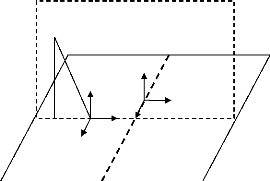
cas des cellules situés sur l'axe (O, Y) car le centre de la cellule sera sur la droite (Oy) se qui se ramène à un angle q i = 90° (figure3 .4, cellule i). De même, pour une cellule située sur l'axe (O,

ð

X), l'angle ö'_i sera de 90° (ou -90°). De plus, l'angle 0, pour la cellule centrale, est de - á.

2

Pour le cas d'une incidence normale, l'angle 0 sera égal à alpha=90°. Ainsi, les résultats obtenus par nos méthodes de calculs correspondent à ces valeurs théoriques.

II

O'

X Cellule i

Z

Oi Y Cellule j

X

Z

Oj Y

Fig.3.4 Cellules particulières dans le réseau

De plus, d'après la figure 3.5, pour la position choisie du cornet, on vérifiera la symétrie pour les différents angles.

100 50 0 -50 -100									40 20 0 -20 -40 30
				q$ i^Oi
										25 20 20 15 10 10 yi 5 00 xi
30 20 1 yi 00				25 20 15 1 5 xi
Représentation 3D de l'angle q$ i									Représentation 3D de l'angleOi
100 50 0 q$ i ' -50 -100 30	20 1 yi	00		5		1		25 20 15 xi	30 20 10 0 O'i -10 -20 -30 30	25 20 20 15 10 10 yi 5 00 xi
Représentation 3D de l'angle q$ 'i									Représentation 3D de l'angleO 'i

Figure.3.5 Représentation 3D des angles

En conclusion, nous venons de vérifier que les deux méthodes nous fournissent une correspondance des valeurs. De plus, nous devons noter que la méthode géométrique nous a permis de vérifier nos calculs car, comme on vient de le remarquer, elle ne peut pas nous fournir les valeurs de tous les angles (l'angle ij '_i ).

2.2 Définition du vecteur champ électrique incident

On utilise la définition au sens de Ludwig 3 [Ludwig73] pour définir le champ électrique incident défini dans le repère lié au cornet. On suppose que le cornet n'a pas de polar croisée. En exploitant la définition de Ludwig et après projection dans la base liée au réseau réflecteur (car

EE=

xréf( ' , ' )

è ö ..

E E

=

y réf( ' , ' )

è ö ..

E E

= ( ' , ' ).sin(').sin(').sin()cos(').si

öè áè

{ ]

[- n('.).cos()cos 2(').cos()}

öáö.á

-

z réf..

? ??

? ??

.sin('). cos('). cos(') cos('). sin(')

{ öè ööö

- }

.. . ..

. sin('). sin('). cos() cos('). sin(').sin()cos ²('). sin()

{ ]

- ?+ -

öè áè öáö}
..

?á

. . .

Eq3.11

c'est dans cette base que sont définies toutes les données de simulation), on obtient l'expression du champ électrique dans la base indiquée.

En fait, on a :

JJJJJJJ_G JJ_G J_G J

^Eè.ö.^{= E}réfè.ö.^?ö . eè+ ö . ö

( ' , ' ) (' , ').sin(').'cos('). '

e?? Eq3.10

?

où est le diagramme du rayonnement de la source primaire (dans notre cas, c'est le

Eréf(?' . ,ij' . )

diagramme de rayonnement d'un cornet qui doit être fourni par la société Alcatel Space).

JJ_G JJ_G JJ_G

Or, en général, un vecteur exprimé par (, dans le repère est

axayaz(o,u _x ,uy,u _z )

, ₎T

JJ_G JJ_G JJ_G

transformé dans les coordonnées (, du repère (

^ar^aè^a ö o, u_r, uè, u ö )

, ₎T au moyen de la matrice

suivante :

? ?

aa

? ? ?

r x

sin().cos() sin().sin() cos()

èöèöè ?

? ? ? ?

? ? =

acos().cos() cos().sin() sin() .

- ?

? ?

èöèöèa

è ? ?

? y

? ? ? ? ?

? ? ?
?

a ? - ? ?

sin() cos() 0

ööa

ö z

De ce fait, les vecteurs '

(e ' ,eö ) sont exprimés dans la base (O',x',y',z') par:

è

eè= cos(è ' . ).cos(ö' . ).e _x + cos(è ' . ).sin(ö' . ).e _y '- sin(è ' . )^.ez ' ' '

eö ' = - sin(ö' . ).e x '+ cos(ö' . ).y e

'

De plus, la projection des vecteurs ' dans la base (O, x, y, z) donne :

(', y , )

^ex^eez'

e z

JJ_G JJ_G

ee

= -
cos().sin(). áá z y
' sin().cos().

? ?

? ??

e= -

y '

e e

x x

'=

e z

áá

e -

y

Donc, en combinant les expressions précédentes on aura :

e_y

JJ_G JJ_G

e =

^è '

cos(' ). cos(' ).cos(' ). sin('). sin() sin('). cos().

è ö è ö áè á

- +

[ ]

. . x . .

e .

?+ ?

. e z

[sin('). sin() cos('). sin('). cos()

è áè öá

- ]
...

? ? JJ

sin(').cos('). sin().cos('). cos().

?

ööáöá

e e e e

ö

= - - -

' . x . y . z
Ainsi, l'expression du champ électrique dans la base liée au réseau réflecteur est la suivante :

2.2.1 Représentation du champ incident en projection

Après avoir pris des cas particuliers pour déterminer d'une façon évidente les différents angles d'incidence et valider nos calculs, nous essayons de représenter le champ incident en projection dans le plan du réseau. Nous considérons déjà que le cornet n'a pas de polar croisé. De la même façon que précédemment, nous avons essayé d'implanter les équations calculées dans notre programme (annexe C) pour encore une fois essayer d'exploiter la représentation du champ incident en projection. Nous devons noter que nous avons multiplié l'une des composantes du champ pour vraiment pouvoir voir clairement la projection de ce dernier pour le cas d'une incidence normale et d'un cornet très loin.

Cornet proche

Cornet très proche

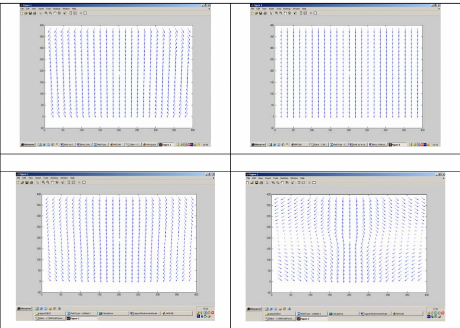
Cornet en incidence normale

Cornet très loin

Figure.3.6. Représentation du champ incident en projection

Nous remarquons que les lignes de champ sont parallèles dans le cas d'un cornet très loin du centre du réseau. Par contre, si le cornet est proche, les lignes de champ commencent à se bomber.