II.5 Diffraction des rayons X et détermination d'une
distance interatomique :
La longueur d'onde des rayons X est du même ordre de
grandeur que la distance interatomique dans les cristaux. La structure
régulière d'un cristal diffractera donc un faisceau de rayons X
de même que les fentes équidistantes d'un réseau
diffractent la lumière. La diffraction par rayons X est un
procédé très puissant pour déterminer la structure
d'un cristal et la distance interatomique (cristallographie).
Les atomes ou les molécules d'un cristal appartiennent
à des familles de plans parallèles (plans réticulaires).
Chaque ensemble de plans parallèles se caractérise par une
distance d entre les plans. Un faisceau parallèle de rayons X
monochromatiques tombant sur le cristal sera diffracté dans toutes les
directions par chaque atome. Les ondes diffractées vont
interférer constructivement dans certaines directions
si elles sont en phase, c'est-à-dire si les différences des
chemins parcourus sont toutes égales à un nombre entier de
longueur d'onde.
On peut montrer que tout se passe comme si le faisceau de
rayons X était réfléchi partiellement par chaque plan
d'une famille (comme pour la réflexion de la lumière, l'angle de
réflexion est égal à l'angle d'incidence), avec la
condition supplémentaire que les faisceaux réfléchis par
les plans parallèles doivent tous être en phase. Ceci n'est
réalisé que dans certaines directions privilégiées
dépendant de la distance d et de la longueur d'onde
ë des rayons X.
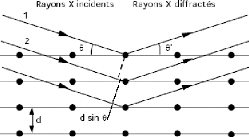
Figure II.4 diffraction des rayons X par une
structure cristalline.
Ainsi, on voit sur la figure (II.4) qu'il y aura
interférence constructive dans la direction
donnée par l'angle è si la différence
entre les parcours des rayons 1 et 2 est égale à
un nombre entier n de la longueur d'onde ë. Il ressort de la
figure (II.4) que ë = 2dsin è, d'où la loi de
Bragg:
2d (hkl) sin è = n ë n = 1, 2, 3...
(II.3)
Connaissant ë, il est possible de déterminer d par la
mesure de l'angle è.
La famille de plans atomiques séparés par la
distance d diffracte le faisceau dans la direction è si cet angle
satisfait la loi de Bragg. [8]
II.5.1 Condition de diffraction:
Les conditions de diffractions sont différentes suivant le
mode d'empilement. On peut montrer que pour une :
-Maille P : tous les plans diffractent.
-Maille I : seul les plans tels que (h+k+l) paire diffractent.
-Maille F : seul les plans tels que h, k, l soient de même
parité diffractent. [9]
II.5.2 Intensité diffracté :
a) Facteur de diffusion:
? sinkr
f = 4 j-j p r r dr
2
f ( ) 41'
Ou k = sin O (II.4)
kr ?
Le facteur de diffusion f d'un atome mesure sa capacité
à diffuser les rayons X.Si ce facteur est grand, cet atome contribue
beaucoup à la diffusion des rayonx X qui provoque la figure de
diffraction. Le facteur de diffusion est relié à la
densité électronique ñ et à l'angle de diffusion
è par:
0
Dans la direction du faisceau (è = 0),f est égal
au nombre d'électrons de l'atome.
b) Facteur de structure:
Le facteur de structure F hkl, est la somme des
facteurs de diffusion des atomes dans une maille cristallographique,
pondérée par un facteur de phase qui dépend de leur
position:
F hkl f i e [I
2 i ( hx i ky i lz
i )
? ?
=
(II.5)
i
L'intensité de la réflexion (hkl) est
proportionnelle à Fhkl 2. [10]
| 


