5.3.3.4. Estimation des paramètres des
modèles développés (calibration ou apprentissage)
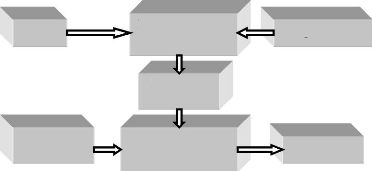
L'apprentissage (ou la calibration) représenté
sur la figure 48 consiste en un entraînement du
réseau. Des entrées (variables) sont présentées au
réseau pour modifier sa pondération de telle sorte que l'on
trouve la sortie correspondante. L'algorithme consiste dans un premier temps
à propager vers l'avant les entrées jusqu'à obtenir une
sortie par le réseau. La seconde étape compare la sortie
calculée à la sortie réelle connue. les poids (weight)
sont alors modifiés de telle sorte qu'à la prochaine
itération, l'erreur commise entre la sortie calculée et
mesurée soit minimisée. Malgré tout, il ne faut pas
oublier que l'on a des couches cachées. L'erreur commise est
rétropropagée vers l'arrière jusqu'à la couche
d'entrée tout en modifiant la pondération. Ce processus est
répété sur tous les exemples jusqu'à ce que l'on
obtienne une erreur de sortie considérée comme acceptable par le
modélisateur. Quand l'erreur devient suffisamment petite, le
réseau ainsi optimisé est utilisé pour calculer les
sorties en introduisant de nouvelles entrées inconnues par le
modèle : c'est la validation (test ou contrôle selon les
auteurs).
Entrées
Nouvelles
entrées
Réseaux de neurone formel (RNF)
Réseau de neurone
formel (RNF)
Déterminer
les poids
Indiquer la sortie
Sortie prévue
Figure 48 : Stratégie
d'apprentissage des modèles neuronaux
L'estimation des paramètres comporte plusieurs choix :
le critère d'erreur à atteindre ; l'algorithme d'optimisation de
ce critère et ; les paramètres de l'algorithme et l'ensemble des
valeurs initiales aléatoires des poids et des biais. Pour ce faire,
certains choix ont été opérés. Avant d'être
développés dans les sections suivantes, ils sont ici
présentés :
i. le critère d'erreur est l'erreur quadratique;
ii. la méthode du gradient de l'erreur (avec un gradient
partiel et le pas du gradient fixé à 0,1) est choisie pour
optimiser les différents modèles développés. ;
iii. la fonction d'activation est la sigmoïde logistique
bornée de 0 à 1 ;
iv. les poids initiaux des réseaux sont fixés
à 0,1
v. le biais est fixé à 0,1.
Toute la puissance des réseaux de neurones
réside dans leur capacité d'apprentissage. Cet apprentissage se
fait par une rétropropagation de l'erreur commise par le réseau
par rapport à la sortie désirée. Il se fait selon une
approche déterministe où les poids sont modifiés
après présentation de l'ensemble ou partie de la base
d'apprentissage. Le critère à minimiser est l'erreur quadratique
moyenne î :
|
MSE = î ( w) = E d -
? ( w , x )
( 2)
|
(20)
|
Où ö est une fonction dépendante
du réseau, w le vecteur contenant les différents poids
et les biais du réseau, x les exemples présentés
aux réseaux et d les sorties désirées. On modifie
le vecteur w de façon à minimiser cette erreur. Pour
l'optimisation des modèles en général et des
modèles hydrologiques en particulier, deux grandes familles de
méthodes existent dans la littérature : les méthodes
locales et les méthodes globales.
5.3.3.4.1. Méthodes locales
La méthode locale exige le choix d'un point de l'espace
des paramètres comme point de départ et le déplacement
dans une direction qui améliore continuellement le critère de
performance. Deux variantes de cette méthode existent. Ce sont les
méthodes directes et les méthodes du gradient. Les
méthodes directes se basent plus sur le choix de la direction et du pas
de recherche. Là encore de nombreuses variantes existent : la
méthode de Rosenbroch (1960), la méthode du Pattern Search (PS),
(Hooke et Jeeves, 1961), la méthode du Simplex (Nelder et Mead, 1965) et
la méthode "pas a pas" (Michel, 1989 ; Nascimento, 1995).
En ce qui concerne les méthodes du gradient, elles
utilisent en plus de la valeur de la fonction critère, la valeur de son
gradient pour décider de la stratégie d'évolution dans
l'espace des paramètres (Perrin, 2000). Dans cette catégorie, on
a les méthodes de 1er ordre (Retro propagation de l'erreur et
ses dérivées) et les méthodes de 2eme ordre
(Gradient conjugué + Fletcher-Reeves (CCGF) et Levenberg-Marquardt
(LM)).
5.3.3.4.2. Méthodes globales
Pour Perrin (2000), les méthodes globales permettent de
traiter efficacement des problèmes
où la fonction à
optimiser est multi modale. Ces méthodes sont différentes des
premières par
le fait qu'elles explorent une partie beaucoup plus grande de
l'espace des paramètres. Trois variantes existent : les méthodes
déterministes, les méthodes stochastiques et les méthodes
combinatoires. Pour plus de détail sur ces méthodes, consulter
les travaux de Perrin (2000). La méthode locale du gradient (la
rétro-propagation de l'erreur) est utilisée dans ce
mémoire. La qualité des paramètres d'un modèle
dépend de la puissance et de la robustesse de l'algorithme
utilisé (Duan et al., 1992). En modélisation,
l'optimisation n'est pas un problème hydrologique mais un corollaire
mathématique lié à la nature et à la
complexité intrinsèque du modèle. Comme mentionné
au chapitre II, les algorithmes d'apprentissage sont des règles à
partir desquelles les modèles neuronaux vont apprendre à se
comporter, à se construire. Ils fonctionnent par minimisation de
l'erreur d'un critère imposé. La méthode du gradient peut
être :
i. totale, dans le cas de l'utilisation d'un critère
total : celui-ci prend en compte tous les exemples en même temps ;
ii. partielle, dans le cas d'utilisation d'un critère
partiel : celui-ci considère chaque exemple pris
séparément.
Cette méthode nécessite l'emploi d'une fonction
sigmoïde dérivable. Elle utilise un développement de Taylor
à l'ordre 1 de l'erreur quadratique. Il a été
développé par Rumelhart et Parkenet le Cun en 1985 et repose sur
la minimisation de l'erreur quadratique entre les débits calculés
et les débits mesurés aux différentes stations. Le terme
rétropropagation du gradient provient du fait que l'erreur
calculée en sortie est retransmise en sens inverse vers l'entrée.
Dans cette méthode, la stratégie de mise à jour des poids
est différente selon qu'on se trouve à la sortie des
réseaux où à l'intérieur de ceux-ci. Pour plus de
compréhension, on considère un réseau comportant n
variables d'entrée, m variables de sortie et plusieurs
couches cachées. Supposons qu'on dispose d'un ensemble d'apprentissage
composé de k paires de vecteurs :
( x 1 , o 1), (
x2, o 2) , ,( xk
,o k) (21)
Avec :
= , 0 , 1 , , 0 , 2 , ..., , 0 , ? (Vecteur d'entrée) ;
n
( ) t
x x x x R
p p p p n
o p = o p , 1 ,
op,2 ,...,
op,m ? R (Vecteur de sortie)
;
m
( ) t
= , , , , 1 , 2 ,..., , , ? (Vecteur des sorties réelles
du réseau)
m
y y y
( ) t
y R
p p l l p p l m
On pose
Cj , k , i : La connexion
entre le neurone k de la couche j-1 et le neurone i de la couche j :
yp,j, k : L'entrée totale du
neurone k pour l'échantillon p de la couche j :
Cj , k,
0=èj,k : Le poids fictif du neurone k de la couche j
correspondant à un biais dont l'entrée
est fixée à 1.
L'entrée totale du k noeud pour la couche j est :
n
y p , j , k = E Wj,k
, i X p,j -1 , i (22)
i
=
0
La sortie de ce noeud sera :
n
|
Out
|
Wj , k ,i X
|
+ è
- j ,
p j i
, 1 ,
|
k
|
(23)
|
i
=
1
X p , j , k =
F(Yp,j , k ) , F
étant la fonction d'activation sigmoïde présentée
ci-dessus.
Pour la mise à jour des différents poids, on pose
que l'erreur commise sur le kième noeud de
sortie est définie par : äp ,k
= O p , k- X p,l , k
2
m m
(24)
Il vient que l'erreur totale est : (
1 1
J = ä p k
2 = O X
- )
, p k
, p l k
, ,
2 k=1 2 k=1
Pour minimiser J, on calcule son gradient par rapport
à chaque poids C, puis on modifie les poids dans le sens du gradient.
Selon qu'il s'agisse des couches de sortie ou des couches cachées,
l'équation de mise à jour des poids est différente. Elle
est facile à mettre en place pour la couche de sortie et plus difficile
dans l'autre cas. La modification des poids est fonction du calcul du gradient.
Ainsi, les poids sur la couche de sortie sont mis à jour de la
façon suivante :
C t
l k j+ 1 ) = C l,k , j
(t )+ ( )(25)- ( t)
=ìOp, k X p,l , k ) f'
frp,l , k * p,l -1 ,j
(26)
Avec ì le pas d'apprentissage compris entre 0 et
1. Finalement :
ep l , k =
(Op,k - Xp,l , k ' ,
, avec ep, l , k l'erreur de signal du
kieme noeud de la couche de
sortie, l'équation des modification des poids :
(27)
(28)
Cl ,k , j ( t + 1
) = C l,k , j ( t ) + ìe
p,l ,k X p,l -1 ,k
En ce qui concerne la mise à jour des couches
cachées
Cl - 1 , j , ( t +
1 ) = C l-1, j, i ( t ) + ì e
X
p,l -1 , j p,l -2
,i
L'un des inconvénients majeurs de cet algorithme est
qu'il risque de converger vers un minimum local de la surface d'erreur,
d'où un choix non neutre des conditions initiales, fixées
à 0,1 pour le poids et le biais.
| 


