Memoire Online - à‰conométrie financière. Une comparaison entre les données boursières et le chiffre d'affaires Paris.

Comme but du travail, la modélisation économétrique apparaît comme un moyen de résoudre le problème en question. La méthodologie ici présente donne les étapes nécessaires pour élaborer des modèles qui puissent expliquer la relation existante (ou non) entre le cours boursier et le chiffre d'affaires des entreprises concernées.

Pour des raisons de simplification, on accepte l'homoscedasticité et le non autocorrélation des résidus. Cette hypothèse nous permet d'estimer les paramètres par le modèle des moindres carrés ordinaires si les séries sont stationnaires.

Pour rendre plus facile les estimations et computations des données le software libre de statistique gretl a été utilisé. Il a été utilisé parce que son usage est libre et parce qu'il possède la plupart des computations des tests et modèles nécessaires pour la modélisation économétrique du présent travail.

Avant d'élaborer le modèle économétrique, deux tests de stationnarité ont été réalisés, un pour chaque variable, afin d'observer les comportements de ces séries temporelles en ce qui concerne la stationnarité. D'après LARDIC et MIGNON (2002), la définition de stationnarité est la suivante:

"Le processus Xt est stationnaire au sens strict si pour tout (t1, t2,...,tn) avec ti € T, i= 1,..., n, et si pour tout ô € T avec ti+ ô € T (Xt, ... Xn) a la même distribution de probabilité jointe que (Xt1+ ô, ..., Xtn+ ô) ".

Comme la définition de stationnarité au sens strict est trop restrictive, nous préférons utiliser celle de Brooks (2008), la définition de stationnarité faible: "(...) can be defined as one with a constant mean, constant variance, and constant autocovariance for each given lag ". Un exemple de série stationnaire et le processus de bruit blanc (BB), qui suit la loi normale avec moyenne et variances constantes. D'après la console du software libre gretl, il' est possible de générer un processus stationnaire, comme celui du tableau, de moyenne et variance égales à 0 et 1 respectivement :

Brooks (2008) nous présente deux types des séries non-stationnaires, les séries de marche aléatoire avec dérive ou sans dérive (elles sont aussi appelées des processus de différence stationnaire - DS), et les séries de tendance stationnaire (TS). Les séries les plus courants en finance sont les séries de marche aléatoire, par exemple une marche aléatoire avec dérive (processus AR(1)) :

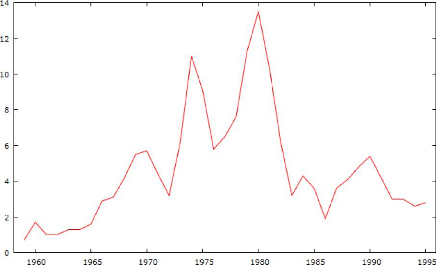
Elles sont décrites comme, d'après Lardic et Mignon (2002) : "Un processus DS est un processus que l'on peut rendre stationnaire par l'utilisation d'un filtre aux différences" i.e. qu'après une différentiation elles seront I(0). Dans son ouvrage de 2008, Wooldridge a un ensemble des données qui sont disponibles sur le site de gretl, comme exemple, d'après son étude sur la consommation américaine entre les années 1959 et 1995, on a l'inflation du période qui ressemble à un processus de marche aléatoire :

Graphique 2 : Inflation aux États-Unis entre 1959 et 1995 (processus de différence stationnaire)

D'autre part on a les processus de tendance stationnaire, un processus divisé en une partie déterministe et en une autre partie stochastique, donnée par :

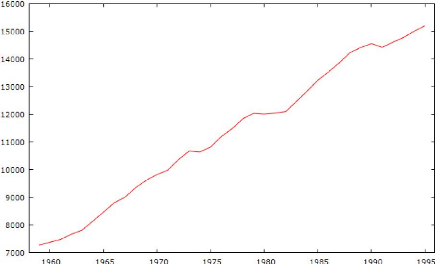
où 8t est une fonction déterministe du temps et où ut suit un BB de moyenne 0 et variance constante. Comme exemple, dans la même étude de Wooldridge, on constate la série de consommation per capita réel qui ressemble à un processus TS :

Graphique 3 : Consommation per capita réel aux États-Unis entre 1959 et 1995 (processus de tendance stationnaire)

Comme, d'après Brooks (2008), les séries financières ont un comportement des séries DS dans la majorité des cas, nous nous concentrons sur ce processus. Il est important, avant de tester la stationnarité des variables, présenter la notion de racine unitaire. Si on prend une série DS et on la généralise pour n'importe quel coefficient de retard (q,), on a :

Ayant cela, on pourrait déduire plusieurs variations sur ce système. Si q, >1, ce qu'on appelle de processus explosif, les chocs au système n'ont pas seulement des effets permanents sur la série, mais des effets croissants (comme les processus explosifs ne sont pas courants en finance, on ne va pas les utiliser description plausible des données). Par contre, si q, est inférieur à l'unité, les chocs vont avoir des effets temporaires, traduit par un cas de stationnarité. Mais si q, est égal à l'unité, les chocs ont des effets permanents, le cas de non stationnarité, c'est ce qu'on appelle aussi de cas de la racine unitaire. Cette notion est utilisée pour les tests de racine unitaire qui cherchent à expliquer si une série est stationnaire ou non.

Le test de racine unitaire utilisé a été le test développé par David Dickey et Wayne Fuller en 1976 (par Fuller) et 1979 (par les deux), le test de Dickey-Fuller dans sa version augmenté (ADF).

Selon Brooks (2008), on constate trois types des modèles de base : (1) le modèle sans tendance ni constante, (2) le modèle sans tendance avec constante et (3) le modèle avec tendance et constante. La tendance présente dans les modèles n'est pas une tendance stochastique, mais déterministe. Pour travailler avec ces modèles, on suppose que les résidus suivent un bruit blanc de moyenne égale à zéro et variance constante et égale à ó2å.

On a comme hypothèse nulle l'existence de racine unitaire dans la série (donc non stationnarité) et comme l'hypothèse alternative la stationnarité, où la racine est inférieure à l'unité. Par exemple, dans le modèle (3) :

On teste si ö est égale à l'unité ou non. Comme attesté par Brooks (2008), pour rendre plus facile la compréhension et l'interprétation, on soustrait yt-1 dans chaque côté de l'équation :

Le test n'utilise pas les valeurs critiques du test t-student, mais les valeurs critiques tabulées par Fuller (1976). Ces valeurs sont plus importantes que les valeurs du test t. D'après Lardic et Mignon (2002), on constate les valeurs critiques pour la racine unitaire :

Tableau 1 : Valeurs critiques de Dickey-Fuller pour l'hypothèse de racine unitaire






	^{Taille 1% 5% 10%}
^{Modèle (1)}
¹⁰⁰	^-2.60	^-1.95	^-1.61
²⁵⁰	^-2.58	^-1.95	^-1.62
⁵⁰⁰	^-2.58	^-1.95	^-1.62
	^-2.58	^-1.95
8
¹⁰⁰	^-3.51	^-2.89
²⁵⁰	^-3.46	^-2.88
⁵⁰⁰	^-3.44	^-2.87
8	^-3.43	^-2.86

Tableau 2 : Valeurs critiques de Dickey-Fuller pour la constante et la tendance temporelle

à‰conométrie financière. Une comparaison entre les données boursières et le chiffre d'affaires Paris.

2. MÉTHODOLOGIE