2.2.2 Analyse descriptive
Pour avoir une idée très fiable sur
l'évolution des données au cours du temps, on s'intéresse
aux statistiques descriptives des données (moyenne, écart type,
minimum, maximum, Skewness et Kurtosis). Le test de normalité des
séries temporelles étudiée dans ce sujet, est basé
primordialement aux coefficients « Skewness », « Kurtosis »
et la statistique du test de « Jarque-Bera ».
Le tableau 1 affiche l'histogramme et les statistiques
descriptives des rendements géométriques de l'indice « MASI
».
600 500 400 300 200 100
0
|
|
|
|
|
Series: MASI
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000206
Median 0.000272
Maximum 0.053054
Minimum -0.092317
Std. Dev. 0.007353
Skewness -1.853794
Kurtosis 30.75269
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 52100.56
Probability 0.000000
|
|
|
|
|
|
|
|
Tableau 1 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
« MASI ».
Dans le premier tableau sont représentés les
différents paramètres statistiques de la série des
rendements géométrique de l'indice « MASI », sur la
période étudiée. On constate que la représentation
graphique de la série des rendements géométriques prend
une forme leptokurtique :
? Le coefficient d'aplatissement (Kurtosis k=
30.75269 est plus grand que 3, celui de la distribution normale. ? Le
coefficient d'asymétrie (Skewness s = -1.853794 #
0) dans le cas d'une distribution normale. Le tableau montre un
coefficient de Skewness significativement négatif, ce qui nous permet de
déduire que la distribution est asymétrique et que la
probabilité d'obtenir des rendements inférieurs à la
moyenne étant supérieure à celle d'obtenir des rendements
plus élevés que la moyenne.
La valeur de la Kurtosis de 30.75269 est largement
supérieure à 3 qui correspond à celle de la loi gaussienne
suggère une queue épaisse de la distribution.
La lecture analytique des paramètres de «
Skewness » et de « Kurtosis »
conduit aux évidentes constations concluent dans les différentes
études des cours boursiers. Généralement, ces coefficients
sont différentes de 0 et 3, ce qui indique que la série des
rendements géométriques du « MASI » est n'est pas
normale mais plutôt asymétrique avec des queues épaisses
caractérisant une distribution leptokurtique. Ce qui nous conduit au
rejet de l'hypothèse de normalité.
De davantage, on représente un récapitulatif de
ces différentes propriétés dans l'histogramme de la
série des rendements, et cela en partageant les rendements journaliers
de l'indice principal du marché boursier. On remarque bien que la
distribution des rendements n'est pas normalement aplatie. Elle a en
particulier des queues de distribution trop épaisses (Kurtosis =
30.75269 > 3).
En outre, le test de Jarque Bera qui donne une p-value
égale à 0,000000 (sous l'hypothèse nulle H0, La
p-value est la probabilité d'obtenir une statistique aussi extrême
(pour ne pas dire aussi grande) que la valeur observée sur
l'échantillon. La p-value à un seuil de confiance
préalablement défini (traditionnellement 5 %). Dans notre cas
p-value < 5% et donc on rejette H0 : les données suivent une loi
normale) pratiquement nulle.
La valeur très élevée de la statistique
de Jarque-Bera (JB) de 52100.56 confirme le rejet de l'hypothèse nulle
de la normalité des rendements géométriques pour cet
indice. Ce qui nous conduit à confirmer la non-normalité de la
série des rendements géométriques de l'indice principal
« MASI ».
Les tableaux (2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9) affichent
respectivement les statistiques descriptives des rendements
géométriques du cours des huit indices sectoriels
étudiés dans ce mémoire (Assurances, Banques,
Télécommunications, Bâtiments & MC, Pétroles
& Gaz, P.P immobilières, Transport et Loisirs & Hôtels).
Ces tableaux incluent aussi les histogrammes des rendements
géométriques des cours de ces indices.
600 500 400 300 200 100
0
|
|
|
|
|
|
|
|
Series: ASSURANCES
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000262
Median 0.000193
Maximum 0.067062
Minimum -0.085039
Std. Dev. 0.013541
Skewness -0.602697
Kurtosis 9.394267
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 2813.821
Probability 0.000000
|
|
|
|
|
|
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 26 sur 113
-0.08 -0.06 -0.04 -0.02 0.00 0.02 0.04 0.06
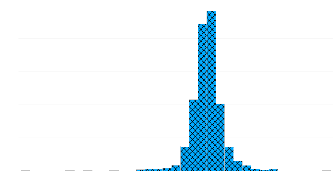
Tableau 2 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Assurances ».
500
400
300
200
100
Le tableau 2 des rendements géométriques de
l'indice sectoriel « Assurances », montre une Skewness
négative de -0.602697 ce qui nous permet de déduire que les
rendements géométriques pour cet indice ont une longue queue
à droite. La valeur de la Kurtosis de 9.394267, est largement
supérieure à 3, (celle de la loi normale), ce qui explique une
queue épaisse de la distribution. La valeur élevée de la
statistique de Jarque-Bera (JB) 8213.821 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MAST
».
Series: BANQUES
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 9.60e-05
Median 0.000204
Maximum 0.065637
Minimum -0.103011
Std. Dev. 0.009099
Skewness -1.379363
Kurtosis 22.21553
Jarque-Bera 25044.63
Probability 0.000000
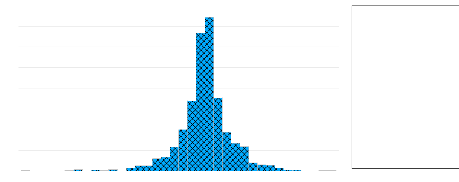
Tableau 3 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Banques ». Le tableau 3 des rendements
géométriques du cours de l'indice sectoriel « Banques
», montre une Skewness négative de -1.379363 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. La valeur de la Kurtosis de 22.21553, est
largement supérieure à 3, ce qui explique une queue
épaisse de la distribution. La valeur élevée de la
statistique de Jarque-Bera (JB) 25 044.63 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MAST
».
400
350
300
250
200
150
100
50
Series: BAT_MC
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000143
Median 0.000182
Maximum 0.070042
Minimum -0.101991
Std. Dev. 0.014411
Skewness -0.529689
Kurtosis 8.092728
Jarque-Bera 1798.240
Probability 0.000000
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 27 sur 113
Tableau 4 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Bâtiment et MC ».
Le tableau 4 des rendements géométriques du
cours de l'indice sectoriel « Bâtiments et MC », montre une
valeur de Skewness négative de -0.529689 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. Le coefficient de la Kurtosis affiche une
valeur de 22.21553, qui est supérieure à 3, celle correspondante
à la loi gaussienne, ce qui explique une queue épaisse de la
distribution. La valeur très élevée du paramètre de
Jarque-Bera (JB) qui est égal à 1798.240 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
600 500
400 300 200 100
|
|
|
|
|
|
|
|
Series: PETROLES &
GAZ
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 0.000551
Median 0.000000
Maximum 0.073292
Minimum -0.087289
Std. Dev. 0.015600
Skewness -0.248322
Kurtosis 7.022547
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 1091.747
Probability 0.000000
|
0
|
|
|
|
|
|
|
|
|
|
|
-0.075 -0.050 -0.025 0.000 0.025 0.050
0.075
Tableau 5 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Pétroles et Gaz ».
Le tableau 5 des rendements géométriques du
cours de l'indice sectoriel « Pétroles et Gaz », montre une
Skewness négative de -0.248322 ce qui nous permet de déduire que
les rendements géométriques pour cet indice ont une longue queue
à droite. La valeur de la Kurtosis de 7.022547, est largement
supérieure à 3, celle correspondante à la loi gaussienne,
ce qui explique une queue épaisse de la distribution. La valeur
élevée de la statistique de Jarque-Bera (JB) 1091.747 confirme le
rejet de l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
300 250
200 150 100
50
0
|
|
|
|
|
|
|
|
|
|
Series: PROMOTION IMMO
Sample 1/05/2016 5/31/2022
Observations 1595
Mean -0.000634
Median -0.000581
Maximum 0.090888
Minimum -0.104202
Std. Dev. 0.019702
Skewness -0.162483
Kurtosis 5.890305
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 562.2020
Probability 0.000000
|
|
|
|
|
|
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 28 sur 113
-0.100 -0.075 -0.050 -0.025 0.000 0.025 0.050
0.075
Tableau 6 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « P.P Immobilières.
Le tableau 6 des rendements géométriques du
cours de l'indice sectoriel « Bâtiments et MC », montre une
valeur de Skewness négative de -0.162483 ce qui nous permet de
déduire que les rendements géométriques pour cet indice
ont une longue queue à droite. Le coefficient de la Kurtosis affiche une
valeur de 5.890305, qui est supérieure à 3, celle correspondante
à la loi gaussienne, ce qui explique une queue épaisse de la
distribution. La haute valeur de Jarque-Bera (JB) = 562.2020 confirme le rejet
de l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que le « MASI
».
700
600
500
400
300
200
100
0

Series: TELECOM
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 6.70e-05
Median 0.000000
Maximum 0.056536
Minimum -0.100845
Std. Dev. 0.009296
Skewness -1.243981
Kurtosis 21.42858
Jarque-Bera 22981.45
Probability 0.000000
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 29 sur 113
-0.100 -0.075 -0.050 -0.025 0.000 0.025
0.050
Tableau 7 : Histogramme et
statistiques du rendement géométrique (log-return) de l'indice
sectoriel « Télécom ».
Le tableau 7 des rendements géométriques du
cours de l'indice sectoriel « Télécom », montre un
Skewness négative de -0.529689, ce qui nous permet de déduire que
les rendements géométriques pour cet indice ont une longue queue
à droite. Le coefficient de la Kurtosis affiche une valeur de 21.42858,
qui est supérieure à 3, celle correspondante à la loi
gaussienne, ce qui explique une queue épaisse de la distribution. La
valeur très élevée du paramètre de Jarque-Bera (JB)
qui est égal à 22981.45 confirme le rejet de l'hypothèse
nulle de la normalité des rendements géométriques pour cet
indice aussi bien que l'indice « MASI ».
900 800
700 600 500 400 300
200 100
0
|
|
|
|
|
|
Series: TRANSPORT
Sample 1/05/2016 5/31/2022
Observations 1595
|
|
|
|
|
|
|
|
|
|
Mean 0.000168
Median 0.000000
Maximum 0.087665
Minimum -0.100192
Std. Dev. 0.016234
Skewness -0.010929
Kurtosis 8.827230
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jarque-Bera 2256.732
Probability 0.000000
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 8 : Histogramme et
statistiques du rendement géométrique de l'indice sectoriel
« Transport ».
Le tableau 8 des rendements géométriques du
cours de l'indice sectoriel « Transport », montre un Skewness
négative de -0.010929, ce qui nous permet de déduire que les
rendements géométriques pour cet indice ont une longue queue
à droite. Le coefficient de la Kurtosis affiche une valeur de 8.8272.30,
qui est supérieure à 3, celle correspondante à la loi
gaussienne, ce qui explique une queue épaisse de la distribution. La
valeur très élevée du paramètre de Jarque-Bera (JB)
qui est égal à 2256.732 confirme le rejet de l'hypothèse
nulle de la normalité des rendements géométriques pour cet
indice aussi bien que l'indice « MASI ».
.
700 600 500 400
300 200 100
0
|
|
Series: LOISIRS &
HOTELERIE
Sample 1/05/2016 5/31/2022
Observations 1595
Mean 1.55e-05
Median 0.000000
Maximum 0.095277
Minimum -0.105171
Std. Dev. 0.024546
Skewness -0.048587
Kurtosis 5.674482
Jarque-Bera 475.9943
Probability 0.000000
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 30 sur 113
Tableau 9 : Histogramme et statistiques
du rendement géométrique de l'indice sectoriel « Loisirs et
Hôtellerie »
Le tableau 9 des rendements géométriques du
cours de l'indice sectoriel « Loisirs et Hôtellerie », montre
un Skewness négative de -0.048587, ce qui nous permet de déduire
que les rendements géométriques pour cet indice ont une longue
queue à droite. Le coefficient de la Kurtosis affiche une valeur de
5.674482, qui est supérieure à 3, celle correspondante à
la loi gaussienne, ce qui explique une queue épaisse de la distribution.
La valeur très élevée du paramètre de Jarque-Bera
(JB) qui est égal à 475.9943 confirme le rejet de
l'hypothèse nulle de la normalité des rendements
géométriques pour cet indice aussi bien que l'indice « MAST
».
Quantile-Quantile QQ-Plot :
Nous utilisons le graphique quantile-quantile QQ-plot pour
vérifier si la série des rendements géométriques du
cours des indices est normalement distribuée.
Le QQ-plot est situé sur une ligne droite à 45
degrés si la distribution empirique est identique à la
distribution théorique (normale).
La figure 10 affiche le QQ-plot de la distribution empirique
des rendements géométriques du principal indice de la B.V.C par
rapport à la distribution normale.
.03 .02 .01
.00
-.01
-.02
-.03
|
|
|
-.10 -.08 -.06 -.04 -.02 .00 .02 .04
.06
Figure 10 : QQ-plot du rendement
géométrique (log-return) du principal indice de la B.V.C.
Quantiles of MAST
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 31 sur 113
Les figures (11 ; 12 ; 13 ; 14 ; 15 ; 16 ; 17 et 18) affichent
respectivement les QQ-plot de la distribution empirique des rendements
géométriques des huit indices sectoriels étudiés,
par rapport à la distribution normale.
.06 .04 .02
.00 -.02 -.04 -.06
|
|
|
-.10 -.06 -.02 .00 .02 .04 .06
.08
Quartiles of ASSURANCES
Figure 11 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Assurances
»
.04 .03 .02 .01
.00
-.01
-.02
-.03
-.04
|
|
|
-.12 -.08 -.04 .00 .04 .08
Quantiles of BANQUES
Figure 12 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Banques
».
.04 .03 .02
.01 .00
-.01
-.02
-.03
-.04
|
|
|
-.12 -.08 -.04 .00 .04 .08
Quantiles of
Télécommunications
Figure 13 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Télécommunications »
.06 .05 .04
.03 .02 .01 .00
-.01
-.02
|
|
|
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 32 sur 113
-.12 -.08 -.04 .00 .04 .08
Cimantiles of BAT MC
Figure 14 : QQ-plot du rendement
géométrique de l'indice sectoriel « Bâtiments &
MC».
.06 .04 .02 .00
-.02
-.04
-.06
|
|
|
-.12 -.08 -.04 .00 .04 .08
Figure 15 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel «
Pétroles & Gaz ».
.08 .06 .04 .02
.00 -.02 -.04 -.06
-.08
|
|
|
Quantiles of PET_GAZ
-.12 -.08 -.04 .00 .04 .08 .12
Quantiles of P.P IMMO
Figure 16 : QQ-plot du rendement
géométrique de l'indice sectoriel « P.P immobilières
».
.06 .04 .02 .00
-.02
-.04
-.06
|
|
|
-.12 -.08 - .00 .04 .08 .12
Qu
anlitiles of TRANSPORT
Figure 17 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Transport
».
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 33 sur 113
.100 .075 .050 .025
.000
-.12 -.08 -.04 .00 .04 .08 .12
Figure 18 : QQ-plot du rendement
géométrique (log-return) de l'indice sectoriel « Loisirs
& Hôtels ».
Quantiles of HOTELLERIE
L'analyse des figures présentées ci-dessus
montre que les rendements géométriques des distributions
empiriques de l'indice principal et des indices sectoriels choisis dans notre
recherche indiquent des écarts des queues plus épaisses que
celles de la distribution normale par rapport à la normale.
Le tableau 10 englobe les statistiques descriptives (moyenne,
écart type, minimum, maximum, Skewness et Kurtosis) des rendements
géométriques du « MASI » et des indices sectoriels
choisis dans notre échantillon.
Indices
|
Moyenne
|
Ecart-Type
|
Minimum
|
Maximum
|
Skewness
|
Kurtosis
|
MASI
|
0,000206
|
0,007353
|
-0,092317
|
0,053054
|
-1,853794
|
30,75269
|
ASSURANCES
|
0,000262
|
0,013541
|
-0,085039
|
0,067062
|
-0,602697
|
9,394267
|
BANQUES
|
0,0000960
|
0,009099
|
-0,103011
|
0,065637
|
-1,379363
|
22,21553
|
BAT_MC
|
0,000143
|
0,014411
|
-0,101991
|
0,070042
|
-0,529689
|
8,092728
|
PET_GAZ
|
0,000551
|
0,015600
|
-0,087289
|
0,073292
|
-0,248322
|
7,022547
|
PROMOIMMO
|
-0,000634
|
0,019702
|
-0,104202
|
0,090888
|
-0,162483
|
5,890305
|
TELECOMU
|
0,0000670
|
0,009296
|
-0,100845
|
0,056536
|
-1,243981
|
21,42858
|
TRANSPORT
|
0,000168
|
0,016234
|
-0,100192
|
0,087665
|
-0,010929
|
8,827230
|
HOTELERIE
|
0,0000155
|
0,024546
|
-0,105171
|
0,095277
|
-0,048587
|
5,674482
|
|
Tableau 10 : Statistiques
descriptives de l'indice « MASI » et des indices de huit secteurs
d'activité étudiés.
On constate, d'après une étude analytique du
tableau des statistiques descriptives, que les huit secteurs d'activité
de notre étude ont enregistrés des baisses dans leurs rendements
géométriques très proches l'un de l'autre, environ 10%
à l'exception des indices sectoriels « Assurances » et «
Pétroles & Gaz » qui ont enregistré respectivement un
rendement minimal de 8.5% et 8.7%.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance
2021-2022 Page 34 sur 113
Pour la volatilité, les écart-types
montrent que :
v Les valeurs le plus volatiles : Le secteur
« Loisirs et Hôtellerie » avec un écart
type de 0.024546 suivi du secteur « Participation et promotion
immobilière » avec un écart type de 0,019702.
v Les valeurs moyennement volatiles sont : Le
secteur « Transport » avec un écart-type de 0.016234 suivi du
secteur « Pétroles & Gaz » avec un écart-type de
0.015600, puis le secteur des Bâtiments et MC.
v Les valeurs ayant une volatilité plus faible
: Le secteur des Assurances avec un écart type de 0.013541 puis
le secteur « Télécommunications » avec
écart-type de 0.009296 en dernier ressort, le secteur Bancaire avec un
écart type de 0.009099.
Les différentes variables de notre étude se
rassemblent dans un point commun est que leurs coefficients d'aplatissement
affichent des valeurs supérieurs à 3 (Kurtosis >
3), ils ont ainsi une distribution leptokurtique plus tranchante
qu'une distribution normale, avec des valeurs concentrées autour de la
moyenne et les queues sont épaisses. Cela signifie une forte
probabilité pour les valeurs extrêmes. Aussi ces variables ont
tous des coefficients d'asymétrie négatifs (Skewnes
< 0), c'est-à-dire une répartition
asymétrique à gauche, la majorité des cours sont
concentrés à la côté gauche de la moyenne.
Les courbes QQ-plots ne sont pas droites et ont des formes en
S. Ceci permet de confirmer les résultats
précédents des statistiques descriptives par
rapport au rejet de la normalité des rendements
géométriques. Les distributions des actifs sont significativement
différentes de la distribution normale au seuil de 5%. L'application du
test Jarque-Bera aux séries des rendements a confirmé la
non-normalité des séries
étudiées.
Les spécifications GARCH adoptées sont
susceptibles d'expliquer une part significative de la non-normalité de
ces séries.
Mohammed EL MASSAADI FSJES-Agdal MSDG/Finance 2021-2022
Page 35 sur 113
| 


