I-3-3 Les méthodes paramétriques :
La méthode de Variance Covariance :
Cette méthode connu aussi sous le nom de méthode
Riskmetrics. Les principales hypothèses simplificatrices consistent
à supposer, d'une part, que les lois de probabilité qui
régissent les distributions des variations des prix de marché
sont normales et, d'autre part, que les instruments présentent un profil
de risque linéaire. Sous ces hypothèses, la matrice de Variances
Covariances peut être appliquée assez directement aux positions
détenues pour calculer la VaR.
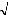
Ainsi, on aura: T
VaR = SCS
Avec:
S = le vecteur des VaR pour chaque position ou facteur de risque=
[... qi ó i ù i ...]
q i = le quantile de la loi normale
ói = la volatilité historique
des facteurs de risque
ù i = la part de la richesse investie dans le
facteur i
C = la matrice des corrélations entre les facteurs de
risque.
Les calculs utilisés dans la méthode RiskMetrics
sont rapides et simples, et requièrent uniquement la connaissance de la
matrice des Variances Covariances des rendements du portefeuille.
Néanmoins, cette méthode s'avère être
inadaptée aux portefeuilles non linéaires (instruments
optionnels), et théoriquement peu adaptée aux queues de
distribution épaisses et aux distributions non normales des
rendements.
La Simulation Monte Carlo :
La méthode de Monte Carlo consiste à simuler un
grand nombre de fois les comportements futurs possibles des facteurs de risque
selon un certain nombre d'hypothèses, et d'en déduire une
distribution des pertes et profits à partir de laquelle on estime
finalement un fractile. Plus précisément, on peut
considérer l'exemple de l'hypothèse de normalité. La
méthode Monte Carlo s'applique en trois étapes:
· La première étape consiste à simuler
N scénario de l'évolution des facteurs de risque. Un
scénario est obtenu à travers la formule suivante:
ÄS = tZ
Avec :
S = le vecteur des facteurs de risque
t = la matrice résultant de la décomposition de
Cholesky de la matrice des Variances Covariances des facteurs de risque ( ?
S = tt' )
Z = un vecteur de variables aléatoires
indépendantes de loi normale centrée et réduite. On
obtient suite à cette étape la série ( Ä S
,...., Ä S
1 N ).
· La deuxième étape consiste à
déterminer les N variations respectives du
N
portefeuille. On obtient donc la suite ( Ä L
,...., Ä L
1 ) des évolutions de la valeur
de la position initiale.
· La troisième étape consiste à
déterminer le quantile de la même façon que pour la
simulation historique à partir de la distribution simulée.
Si cette approche peut s'appliquer, en théorie, quelles
que soient les lois de probabilité suivies par les facteurs de risque,
elle est couramment utilisée en pratique, pour des raisons techniques,
en supposant que les variations relatives des paramètres de
marché suivent des lois normales. Cette méthode convient
également à tous les types d'instruments, y compris optionnels,
et permet de tester de nombreux scénarios et d'y inclure explicitement
des queues de distribution épaisses (événements
extrêmes pris en compte dans une certaine mesure) (voir Glasserman et al.
(2001))
Méthodes basées sur les modèles
GARCH
La méthodologie d'estimation de la VaR en se
basant sur la modélisation GARCH est largement étudiée en
littérature (voir par exemple Christoffersen et al. (2001), Engle
(2001)). En ce qui concerne la détection de l'effet ARCH dans la
série des observations, deux principaux tests complémentaires
peuvent être effectué. Le premier s'intéresse au
phénomène d'auto corrélation entre les termes d'erreur au
carré du modèle : Test Q (p) de Ljung-Box (1978). Si le processus
est ARCH, les résidus au carré doivent être
corrélés. L'hypothèse nulle est l'absence d'auto
corrélation d'ordre p. La statistique du test est supposée suivre
une loi ÷2 avec p degrés de liberté. Le deuxième test
d'intéresse plutôt au phénomène
d'homoscédasticité (constance de la volatilité des termes
d'erreur): Test ARCH (p) d'Engle (1982). Ce test vérifie l'absence
d'hétéroscédasticité autorégressive
conditionnelle d'ordre p. Si le processus est ARCH, les résidus au
carré doivent être hétéroscédastiques.
L'hypothèse nulle est celle de l'homoscédasticité. La
statistique du test est supposée aussi suivre une loi ÷2 avec p
degré de liberté. La règle de décision est la
même pour les deux tests: accepter H0 si la statistique du test est
inférieure à la valeur critique de la loi ÷2 avec
p degrés de liberté à un niveau de confiance donné.
Notons que pour tester l'effet GARCH (p, q), il suffit de procéder
à un test d'effet ARCH (p+q).
La prévision de la Value-at-Risk à partir d'un
modèle GARCH est effectué selon une démarche indirecte:
dans un premier temps, on fait une hypothèse sur la distribution
conditionnelle des rendements de l'actif, puis l'on estime les
paramètres du modèle GARCH sur les observations de la
période 1 à T, généralement par une
procédure de type maximum de vraisemblance. Dans une seconde
étape, on déduit du modèle GARCH estimé une
prévision de la variance conditionnelle, qui couplée à
l'hypothèse retenue sur la distribution des rendements, permet de
construire une prévision sur le fractile de la distribution de pertes et
profits valable pour T+1.
Considérons l'exemple d'un modèle GARCH sous
hypothèse d'une distribution quelconque (normale, student...) de
paramètre v.
On suppose ainsi que les rendements d'un actif, notés
rt , satisfont le modèle suivant :
rt = c+
åt
åt = ztó t
2 2 2
1
-
ót = á0 +
á1 å t- 1 +â1ó t
Les sont indépendantes identiquement distribués
selon la loi mise en hypothèse. Les
zt
paramètres á0 ,
á1 , â1 ,c sont des
réels à estimer vérifiant les contraintes suivantes:
á0 >- 0 , á1 = 0 , â1 = 0
(v peut aussi faire partir des paramètres à estimer
comme dans le cas de la distribution de student).
Le terme ( \ t -1 ) désigne la variance conditionnelle du
résidu
ó t 2 = E å t å
åt et donc des
rendements . Une fois les variables sont estimées (par la
méthode de maximum de
rt
vraissemblance par exemple), on obtient l'expression suivante:
|
? 2 ?
|
? ?
|
|
ó
|
2 2
t +1 = á0 +
á1 åt +
â1ó t
|
Avec 2
ó1 donné et donc :
ó t 1 á á ( r t c
) â ó t 2
= + - +
2
+ 0 1 1
Soit ( , ) la fonction de répartition de la loi de . La
Value-at-Risk pour t+1 et pour un
G 1 á v
- zt
niveau de confiance 1-a obtenue par la formule suivante:
? ? ? ?
VaR t + 1 = ó t+1 G-1
(á , v) + c
| 


