Linéarisation entree sortie et réglage flou d'une machine asynchrone avec pilotage vectoriel et observateur à mode glissant

CHAPITRE III

COMMANDE NON LINEAIRE DE LA

MACHINE ASYNCHRONE

CHAPITRE III: COMMANDE NON LINEAIRE DE LA

MACHINE ASYNCHRONE

III-1. Introduction

Dans ce chapitre nous présentons quelques rappels sur la linéarisation pour des systèmes non linéaires. Ce principe permet le développement d'une commande non linéaire pour le contrôle du couple et du flux en tenant compte d'une limitation de courant. Il permet entre autre de découpler parfaitement le flux et le couple de la machine.

Cette méthode à été développée par Fliess (1982) [18] et elle est présentée dans sa forme actuelle en temps continu dans Isodori (1989) [19].

Nous rappellerons les techniques de commande non linéaire qui font recours à la géométrie différentielle pour linéariser le comportement entrée/sortie d'un système non linéaire.

Nous présentons les lois de commande non linéaire relative aux systèmes mono variables SISO (Single Input Single Output) et multi-variables MIMO (Multi Input Multi Output).

Enfin, nous appliquerons ces techniques à la commande de la machine asynchrone alimentée en tension, et on termine notre chapitre par des simulations qui illustrent le comportement de la commande non linéaire.

III-2. Système mono entrée mono sortie (S.I.S.O) Considérons le modèle non linéaire de la forme suivante :

& = +

( ? ) = x f (x) g(x) .u

(III-1)

y h(x)

=

Ou n

x ? Ret f(x), g(x), h(x) sont des fonctions dérivables.

Le but de l'application de la méthode de linéarisation est de trouver une commande de type retour d'état non linéaire.

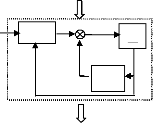
u = á(x) + â (x).v (III-2)

Qui en boucle fermée ramène le système (Ó) non linéaire à un système linéaire (Fig III-1) par rapport à une linéarisation autour d'un point de fonctionnement, ceci permet d'obtenir un comportement linéaire du système sur toute « la plage de fonctionnement » [20, 21,22].

Deux cas peuvent se présenter :

É Le degré relatif (i.e. le nombre de fois qu'il faut dériver la sortie y pour faire apparaître l'entrée u) est égal à l'ordre n du système.Le système peut donc être linéarisé exactement.

É Le degré relatif est strictement inférieur à l'ordre du système, le système est partiellement découplé.

Pour définir les conditions de linéarisation on doit d'abord définir les notions de dérivée de Lie et de crochet de Lie.

- Dérivée de Lie

La dérivée de Lie d'une fonction h(x) le long d'un champ de vecteurs

f(x) = (f₁(x),f₂(x),f₃(x), ,f _n (x) ^t est donnée par :

n ? h L h(x) i f ?= ? = f i 1 i x	(	x)	(III-3)
- Crochet de Lie Le crochet de Lie de f(x) et de g(x) est le champ de vecteur défini par : n n ? g(x) ? f (x) [ ] f, g = ? = ? = f (x) - g (x) L g (x) L f(x) i f g = - 1 x i 1 i ? x i 1 i ?				(III-4)

Afin de définir la loi de commande non linéaire nous calculons le degré relatif de la sortie :

? h ? h

y= x = ?x? x

[f(x) g(x)u]

+

& & (III-5)

L'équation devient :

& y = L _f h(x) + L _g h (x)u (III-6)

Si L _g h(x) ? 0 n

? x ? R , on montre aisément que la commande :

1 u = L h g

(

x)

( L h(x) v) - + f

(III-7)

Conduit au système linéaire représentant un simple intégrateur

& y=v (III-8)

Si L_gh(x) = 0, on continue la dérivation pour obtenir

y L h(x) L L i 1 h(x) .u

i = + i=1,2,... (III-9)

i -

f g f

Avec L L i 1 h(x) 0

g f ?

- . La méthode consiste donc à déterminer le degré de dérivation ä

à partir duquel le coefficient multiplicateur de la commande `u' (L L i 1 h(x))

- n'est pas nul.

g f

ä : est le degré relatif de h(x).On montre que pour y L h(x) L L ¹ h(x) .u

ä = ä + ä - (III-10)

f g f

La commande

1 u 1 = L L h( ä? g f

x)

( L h(x) v) - ä + f

(III-11)

Conduit au système linéaire équivalent à une chaîne de ä intégrateurs :

y = v

^ä (III-12)

Le schéma synoptique pour les différentes étapes de calcul est le suivant :

u	?		y

?.... ?

v

y

x)

u

â(

?

+

á(x)

v

y

Fig III-1. Linéarisation entrée-sortie