III-4-2. Choix des sorties
Le choix des sorties est lié aux objectifs de la
commande. On désire commander le couple et assurer le contrôle du
flux rotorique afin d'éviter la saturation magnétique et de
pouvoir travailler en régime de survitesse ou la limitation de la norme
de la tension impose de baisser la norme du flux.Les sorties sont le couple et
le flux rotorique :
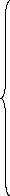
? M
? h (x) ? p
1 ?
Y(x) = r
?? h (x) ?? = L
?
2 ? ?
) ?
?
?
??
2
2
+ x
4
x 3
( x x x x
2 3 1 4
-
(III-20)
III-4-3. Linéarisation entrée-sortie
La condition permettant de vérifier si le système
non linéaire admet une linéarisation E/S est la
détermination du degré relatif.
a) Degré relatif à la sortie Y1 (x)
Y (x) h (x) L .h (x) L h (x) .u
& 1 = & 1 = f 1 + g 1 (III-21)
Le degré relatif associé à Y1
(x) est r1=1
b) Degré relatif à la sortie Y2 (x)
& &

(
x)
(
Y 2
x) h (
= 2
x) L
= f
.h 2
& & &&
(
(III-22)
+
(
) .u
x)
(x
x)
h 2
x) h
= 2
Y (
2
.L f
.h 2
L 2
f
L g
Le degré relatif associé à Y2 (x)
est r2=2
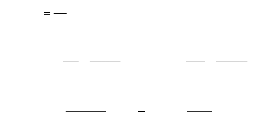
Avec :
|
L h
f 1
|
(
|
x) p
= -
|
M
Lr
|
?
??
|
(
|
1
+
Tr
|
ë
|
)(
|
x2
|
x3
|
-
|
x1
|
x ) p
4 r
+ Ù
|
(x1
|
x x x ) pk
3 2 4
+ + Ù
|
r 3
(x 2
|
+ x 2
4
|
?
) ??
|
x
1
)(
(
2
Tr
L h
f 2
x)
2
x
3
)(
2
T
2k M
+
2
T
+
2
2
T
T
r
r
r
r
+
x )
4
2
2M
2
T
)
2
+x
2
2
T
[ M(x x x x ) (x x )]
2
1 3 2 4 3
+ - +
2
4
L2
f
h(
2
2
+x
4
6M
x
3
4
2MP
Ù
r
(x
2
x
3
x
1
(x
1
2
x) (
=
2k M
) (
-
+ +
x x )
24
|
r
Lgh1(x) =[-pkx4
pkx3]
L L h (x) = 2R kx 2R kx
g f 2 [ r 3 r 4 ]
|
r
|
Le choix de ces sorties aboutit à une linéarisation
partielle d'ordre 3 (r1+r2 p n=5) et une dynamique interne d'ordre
2. (n : ordre du système)
III-4-4. Transformation difféomorphisme
Avec un changement de coordonnées d'ordre rj - 1 et une
transformation z = T(x) [24,26,27], on aura :

h2
(
x)
z
2
z L h
3 f 2
=
x)
(
z arctg (x / x )
4 3 4
=
z x
5 5
=
(III-23)
z4 et z5 peuvent êtres choisis
arbitrairement [24, 26]
Dans le nouveau système de coordonnées, le
modèle (III-23) s'exprime de la façon suivante :
& z 1 =Lfh1(x)+Lgh1(
& z 1 =Lfh1(x)+Lgh1( x)
x)
z & 2 = z 3 (a)
(x ) .u
z L h 2 (x) L g L f h 2
& 3 = f +
2

z
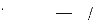
R r
+
z p.z
4 5
=
p
( )
z z
1 2
(b) (III-24)
1 f
( ) 5
=
r
5 2 r
z C z
- -
J J
III-4-5. Loi de commande non linéaire
Pour avoir une linéarisation partielle E/S d'ordre trois
en boucle fermée, il faut appliquer le retour d'état non
linéaire.
x) [ ( v v ) t A(x)]
- (III-25)
1 2

L L h
g f 2
1
x3
? ? ?
x)
-
1
1
-
(
x)
?
?
= ? ? ? ?
r (III-26)
x4
? ? ? ? ? ?
? ? ?
1
2Rk
1
2
r
Ö
(
L h
g 1
pk
1
pk
2R k
r
x4
x3
u D (
= - 1
D (x)
- 1 =
(III-28)
La matrice D-1(x) existe si Ö r ? 0
?
??
A(
x)
|
L h (
2
f 2
f 1 (III-27)
|
x)
|
x)
?
??
L h (
Les composantes du vecteur d'état non linéaire sont
définies comme suit :

h
(
2
?
?
??
2
-
x
4
?
?
? ?
x
3
x
4
?
?
?
?
?
? ?
x)
1
=
?
?
? ?
U
k
Ö
x
3
1
-
2
L
f
p
L 2
f
h (
1
x)
r
v
v
2R
r
s â
?
?
??
U
s á
V1
Lfh1 (x)
u
sá
u
sâ
Is, Ör, X5
D(x)-1
V2
Lfh2(x)
En supposant la matrice de découplage D(x) inversible
:
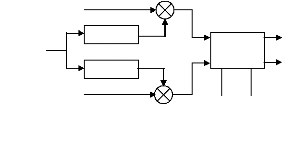
L'application de la loi (III-28) au système
d'équation (III-24) aboutit au modèle linéarisé
(III-29) schématisé par la figure III-5.
|
&
z v
1 1
=
&
z z
2 3
=
&
z v
3 2
=
|
(III-29)
|
|
&
v1 = z
|
|
|
|
|
z1 = Ce
|
|
|
1
|
|
1
s
|
|
|
|
|
|
|
&

3
v2 = z
2
r
z2 = Ö
&
z3 = z2
1
s
1
s
Fig III-5. Système découplé et
linéarisé
Le système (III-24b) est inobservable, donc il faut
montrer que la dynamique des zéros est stable. Pour éviter la
singularité, on choisit z2 ? 0.
La dynamique des zéros devient
&
1
f r
&
= -
z5
J
? + ?
? C z ?
r 5
? J ?
(III-30)
( )
z z
1 ref 1
-
( 2ref 2 ) 22 ( 2ref 2 ) 2ref
z z k z z z
- + - +
& & & &
v 1 k11
v 2
k21
+ z & 1ref
(III-31)
z4 : représente l'angle du flux rotorique
compris entre zéros et 2 ð
d
s =
dt
z5 : est une dynamique du premier ordre
1
z 5 C
f J
+ s
=
Avec une entrée C r physiquement bornée,
z5 reste bornée.
La dynamique est stable (pôle = - f )
J
| 


