IV-3 Modèle de la machine
Le comportement dynamique de la machine asynchrone
alimenté en tension est décrit par un système
d'équations non linéaires, multivariables et fortement
couplées.
.
x 3
Rr
Lr
Le modèle de la machine dans le référentiel
d-q choisi de tel manière que le flux rotorique possède une
composante nulle selon l'axe q est donné par les équations
d'états suivantes :
X & = F(X) + G.U (IV-7)
sl T x
T Ö
R r r4
Avec : [ ]T
g 1 (x) = 1 ó .L s 0 0 0 , [ ]T
g 2 (x) = 0 1 ó.Ls 0 0
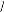
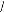
F(x) f (x) f (x) f (x) f (x) x x x x
= =
[ ] [ ]T
T
1 2 3 4 1 2 3 4
U=(U s á U s â ) T
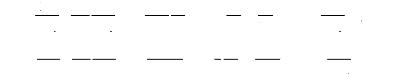
+
+
Rs
Ls
ó .
Rr
.L s
ó
x 3
M x
R .
r x + +
3 r 2
R x
L r
x 1
x 2
x 3
.
R r
x 4
x 3
x 4
.u ds
+
ó
x (
& = -
1
ó
x -
2
ó .L ó .
s
.L s
L 2
r
M
Rs
x (
& = -
2
.L S
1
).
M
L r
2
M
L 2
r
2
M
L 2
r
).
x1
+
ó
L s
+ x 1
x 4
.u qs
+
ó .
(IV-8)
1
.L s
1
M
LL
S r
R r
Cr

J
x1
M.
Rr
Lr
.
x2
x3
J
Lr
1
M

&
x3
&
x4
-
-
Le couple électromagnétique développé
par la machine est donné par : M
C = Ö (IV-9)
elm I
dr qs
r
L
· Choix des sorties : on choisis
comme sortie x3(composante du flux rotorique selon l'axe d) et x4 (la
vitesse).En pose :

1
2
h
h
(
(
Rr
r (IV-10)
r
-
J
= ? 1
?
? ? J
? R r
? L r
Lr
M
Mx
x2
1
x3
? ? ? ?
? ?
L
x3
C
Y(
x)
?
??
?
??
x)
x)
·

.
x)
(
(
x) h
=
1
L
f
Y
1
(IV-11)
& & & &
x)
x ).u
h
1
+
(
Y
1
x) h
=
1
2
L h (
f 1
Lh(
f1
L
g
(
(
x)
x)
Linéarisation entrée-sortie :
la condition permettant de vérifier si le système non
linéaire admet une E/S est la détermination du degré
relatif.
a) Degré relatif à la sortie Y1 (x)
& &
Le degré relatif associé à Y1 (x)
est r1=2 b) Degré relatif à la sortie Y2 (x)
& &

(
x)
x)
(
Y (
2
x) h
= 2
& & & &
(
(IV-12)
Lf
.h 2
+
).u
(
x)
(x
x)
h2
x) h
= 2
Y (
2
.h 2
L 2
f
.Lf
Lg
Le degré relatif associé à Y2 (x)
est r2=2
Delà, on a vérifié que le vecteur
degré relatif est (2,2), ce qui permet d'affirmer que le système
décrit par diffeomorphisme et bouclage est complètement
linéarisable.
IV-4. Application de la commande linéarisante au
moteur
Le changement de coordonnées non linéaire
nécessaire est donné par le système d'équations
suivant [26,27]:
|
z
1
|
h (
1
|
x)
|
=
|
x
3
|
|
z
2
|
L
f
|
h (
1
|
x)
|
f (
3
|
x)
|
(IV-13)
|
z
3
|
h(
2
|
x)
|
=
|
x
4
|
|
z
4
|
L
f
|
h(
2
|
x)
|
f (
4
|
x)
|
Et la matrice de découplage par :
? MR ?
r
? 0 ?
óLL
? ?
s r
D(x) = (IV-14)
? Mx?
? 3
0 ?
? J L L
ó ?
? s r?
L'application du changement de variables (IV-9) au système
d'équations (IV-7) aboutit à l'écriture suivante :
&
z z
1 2
=
|
z L h
2
& 2 f
= 1
&
|
(
|
x)
|
+= L L h (x)u v g f 1 1 1
|
(IV-15)
|
z z
3 4
=
+= L L h (x)u g f 2 2
v2
&
x)
(
z
4
h2
L 2
f
La commande linéarisante est finalement donnée par
:
u D (x) [ ( v v ) t A(x)]
= - 1 - (IV-16)
1 2
? L h (x)?
1 1
u D (x)
- + -
? f
= - 1 ? D (x) .v (IV-17)
2
?? L h (x) ?
f 2 ?
?
?
??
A(
x)
(
x)
?
?
??
L2h
L2
x)
h(
2
f 1 (IV-18)
f
(IV-19)
Avec :

(
Rr
x)
Lh
2
f 1
Lr
( )
Mf ( x ) f ( x )
1 2
-
(
x)
Lh
2
f 2
M

( x f ( x ) x f ( x ) )
JL
3 2 2 3
+
r
- Calcul des trajectoires de
référence :
Les entrées v1, v2 peuvent être calculées de
la façon suivante [24,26,27].
|
v
|
1
|
k
11
|
( ) ( )
z z k z z
- + -
& &
1ref 1 12 1 ref
|
+ z & &
1ref
|
|
v k z z k z z z
2 21 ( 3 ref 2 ) 22 ( 3 ref
3 ) 3 ref
= - + - +
& & &&
Les équations d'erreur de poursuite deviennent :
|
(IV-20)
|
e k e k
& & &
+ +
1 11 1 12
e 0
=
1
, e k e k
& & &
+ +
2 22 2 21
e 0
=
2
| 


