Optimisation des conditions de culture des lipases chez une souche bactérienne de type Actinomadura Keranitilytica par RSM

CHAPITRE 3 : RESULTATS ET DISCUSSION

3.1.2. Résultats du plan de criblage et interprétation ? Traitement et analyse statistique des données

Le traitement des données a été effectué par régression linéaire multiple à l'aide du

logiciel Minitab. Les valeurs des effets et les coefficients de régression du modèle sont donnés dans le (tableau 8).

Tableau 8: Effets et coefficients estimés pour la réponse

Terme	Effet	Coefficient	Probabilité (P S á = 0.05)
Constante	-	51	0,003
X1	32,00	16	0,029
X2	34,33	17	0,025
X3	08,67	4	0.260
X4	27,67	13	0,038
X5	08,67	4	0,260
X6	- 06,67	-3	0,354
X7	- 04,00	-2	0,547
X8	00,00	0	1,000
X9	- 08,00	- 4	0,287
X10	- 05,00	- 2	0,464
X11	- 09,67	- 4	0,225

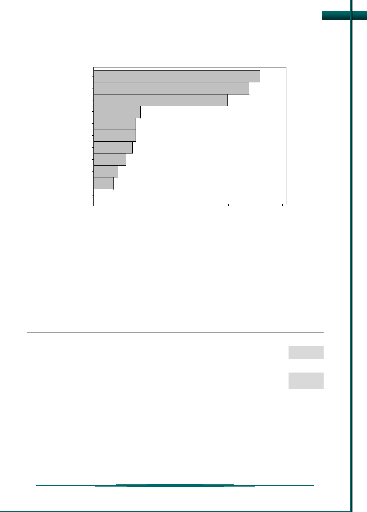
Les résultats du traitement du plan de Plackett-Burman obtenus montrent que parmi tous les facteurs étudiés, seule la température, le temps et le Tween 80 qui ont une influence

36

^t

^T°

^{TWEEN 80}

^(NH2)4SO4

^pH

^FeSO4

^K2HPO4

^CaCL2

^KH2PO4

^NaCl

^MgSO4

⁰

¹

²

³

⁴

⁵

⁶

⁷

CHAPITRE 3 : RESULTATS ET DISCUSSION

significative sur la réponse au niveau de confiance choisi (á = 0,05). L'effet de cette influence schématisée par le diagramme de Pareto (figure 10).

Figure 10 : Diagramme de Pareto des effets des variables explicatives.

L'examen du tableau d'ANOVA (tableau 9) montre que les effets principaux ne sont pas significatifs. Le modèle de premier degré ne peut être donc utilisé comme un modèle d'optimisation car les facteurs ne peuvent pas expliquer la réponse de façon linéaire. Le test du défaut d'ajustement qui est significatif au niveau á = 0,05 confirme cette non linéarité (Courbure avec P = 0,01 < á = 0,05 et valeurs résiduelles importantes).

Tableau 9 : Analyse de variance pour l'activité lipasique

Source	DL	SC	CM	F P
Effets principaux	11	10084	918	10	0,096
Erreur résiduelle	2	3072	3072
Courbure	1	9526	9526	102,43	0,010
Erreur pure	2	0,1	0,04
Total	14	21532,9

En conclusion, nous avons trouvé un modèle significatif qui permet d'avoir une idée préliminaire sur l'influence des différents facteurs. Cependant, les valeurs résiduelles importantes et le manque d'ajustement observé, montrent que le modèle linéaire ne peut pas décrire correctement le phénomène étudié et que d'autres termes importants, comme des

37

CHAPITRE 3 : RESULTATS ET DISCUSSION

interactions ou des termes quadratiques ne doivent pas être exclus. Par conséquent, nous avons décidé de passer à un modèle du second degré du type :

y=b0+?bixik+??bijxikxjk+?bikxik²+ îk... (2)

La question qui se pose alors, concerne le plan de second degré à utiliser et le choix des facteurs qu'il faut maintenir dans l'étude. Parmi les nombreux plans d'expériences du second degré, nous avons choisi le plan de Box-Behnken qui ne nécessite pas un grand nombre d'essais. Nous avons choisi aussi ce plan pour la facilité de sa mise en oeuvre. Concernant le choix des facteurs, nous nous sommes basés sur les résultats du plan de criblage mais également sur des critères expérimentaux. Il ne faut pas perdre de vue que le critère expérimental, basé sur des considérations techniques et scientifiques, est toujours privilégié par rapport aux critères purement statistiques (J.Goupy, 2005).

Ainsi, parmi les onze facteurs introduits au départ dans le plan de criblage, les valeurs de

huit d'entre eux ont été fixées et les trois autres significatifs sont conservés dans le plan de Box-Behnken.

En conclusion, les trois facteurs retenus pour le plan de Box-Behnken sont la température,

le temps (t) et la source de carbone (Tween 80). Ces facteurs ainsi que le domaine de variation, sont précisés dans le (tableau 10) :

Tableau 10 : Facteurs et domaine d'élude du plan de Box-Behnken.

Facteurs	Niveau bas (-1)	Niveau haut (+1)
Température (X1)	40	50
Temps (X2)	2	5
Tween 80 (X3)	2	4

3.1.3. Plan d'optimisation

Le plan de Box-Behnken pour trois facteurs, composés de quinze essais dont trois au

centre du domaine, ainsi que la réponse expérimentale «Activité U/ml », sont donnés dans le (tableau 11) :

38

CHAPITRE 3 : RESULTATS ET DISCUSSION Tableau 11 : Plan de Box-Behnken et les résultats expérimentaux obtenus.

Essai	X1	X2	X3	Activité U/ml
1	50	5,0	3	112
2	45	5,0	4	138
3	40	3,5	2	73
4	45	5,0	2	107
5	45	2,0	4	62
6	45	3,5	3	149
7	50	3,5	2	84
8	45	3,5	3	144
9	45	2,0	2	53
10	40	2,0	3	25
11	50	2,0	3	45
12	40	3,5	4	75
13	45	3,5	3	159
14	50	3,5	4	87
15	40	5,0	3	95

Le plan de Box-Behnken pour trois facteurs, composés de quinze essais dont trois au centre du domaine, ainsi que la réponse expérimentale «Activité U/ml », sont donnés dans le (tableau 11).

Le traitement statistique des données du (tableau 11) à l'aide du logiciel Minitab, permet d'estimer les coefficients du modèle (cf. eq.1) (tableau 12).

39

CHAPITRE 3 : RESULTATS ET Tableau 12 : Coefficients estimés pour l'activité U/ml
			DISCUSSION
Terme	Symbole	Coefficient	Probabilité
Température	X1	39,96	0,000***
Temps	X2	126,77	0,004***
Tween 80	X3	282,54	0,008***
Température*Température	X1^2	- 0,070	0,000***
Temps*Temps	X2^2	- 7,03	0,000***
Tween 80 * Tween 80	X3^2	0,0027	0,002***
Température*Temps	X1?X2	-0,01	0,854 ^NS
Temperature*Tween 80	X1? X3	0,01	0,951 ^NS
Temps* Tween 80	X2? X3	2,44	0,251 ^NS

*** : corrélation très hautement significative au niveau de confiance de 99% (P<0.001). NS : non significative. R² = 98,7%, R²aj. = 96,3 %.

Nous remarquons à travers l'analyse du (tableau 12) et celle de l'ANOVA (tableau 13), que les facteurs principaux et quadratiques ont des effets hautement significatifs, contrairement aux effets d'interactions entre facteurs. La non signification des interactions entre facteurs montre que l'effet d'un facteur ne dépend pas du niveau de l'autre.

Tableau 13 : Analyse de variance pour l'activité U/ml

Source	DL	SC	MS	F P
Régression	9	22700	22700	42 0,000***
Linéaire	3	9614	7978	44 0,001***
Carré	3	12960	12960	72 0,000***
Interaction	3	124	124	0,7	0,599 ^NS
Erreur résiduelle	5	300	300
Inadéquation de l'ajustement	3	184	184	1,05	0,522 ^NS
Erreur pure	2	117	117
Total	14	23000

*** : corrélation très hautement significative au niveau de confiance de 99% (P<0.001). NS : non significative.

40

²⁰

⁴⁰

⁶⁰

⁸⁰

¹⁰⁰

¹²⁰

¹⁴⁰

¹⁶⁰

CHAPITRE 3 : RESULTATS ET DISCUSSION

A partir des résultats obtenus ci-dessus (tableau13), nous avons obtenu un modèle très hautement significatif qui met en évidence la relation entre les facteurs expérimentaux et la réponse. Le modèle obtenu après extraction des variables non significatives et négligeable, se présente comme suit :

Activité = 6770 + 39,96 X1 + 126,77 X2 + 282,54 X3

La probabilité d'inadéquation de l'ajustement augmente de 0,522 montre que le modèle obtenu explique bien le phénomène étudié. A partir de ces résultats on procède à la validation du modèle et l'optimisation des variables explicatives.

? Validation primaire du modèle

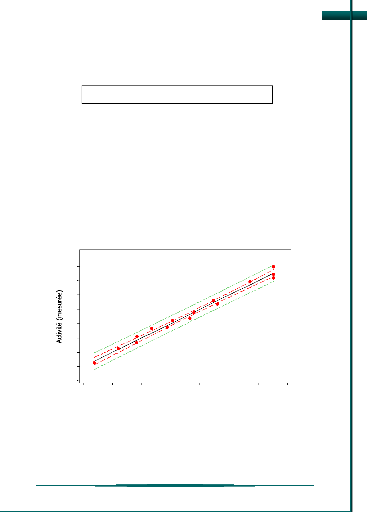
La validation primaire du modèle consiste à s'assurer que les réponses calculées et mesurées se corrèlent significativement. Le diagramme des réponses mesurées, en fonction des réponses estimées, montre une forte corrélation entre celles-ci (figure 11). Le modèle rend, donc, bien compte du phénomène étudié.

R2 = 99%

^{Activité (estimée)}

Figure 11 : Diagramme des réponses mesurées en fonction de celles estimées.

41

¹⁸⁰

¹⁶⁰

¹⁴⁰

¹²⁰

¹⁰⁰

⁸⁰

⁶⁰

⁴⁰

²⁰

⁰

CHAPITRE 3 : RESULTATS ET DISCUSSION

? Optimisation de l'activité

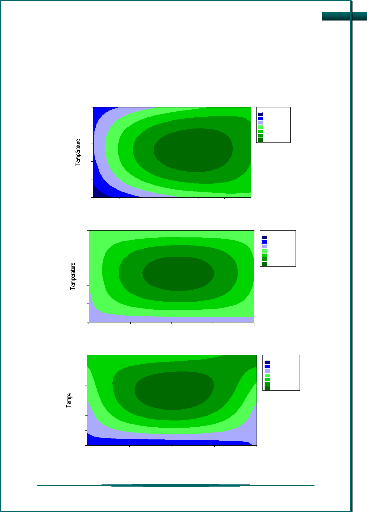
La recherche des conditions optimales, qui permettant d'aboutir à une meilleure activité enzymatique, a été réalisée par l'analyse des diagrammes de contour (figure 12) qui sont les projections des courbes tridimensionnelles des surfaces de réponse. Ces dernières sont générées par le logiciel Minitab par la combinaison des trois facteurs.

⁵⁰

^y

⁴⁸

< ^{40 40} - ^{60 60} - ^{80 80} - ^{100 100} - ^{120 120} - ¹⁴⁰

⁴⁶

⁴⁴

⁴²

⁴⁰

^2,0

^{4,5 5,0}

^{3,5 4,0}

^{2,5 3,0}

^Temps

⁵⁰

^y

¹⁴⁰

⁴⁸

>

< ^{40 40} - ^{60 60} - ^{80 80} - ^{100 100} - ^{120 120} - ¹⁴⁰

>

⁴⁶

⁴⁴

⁴²

⁴⁰

^4,0

^3,5

^3,0

^2,5

^{Tween 80}

^5,0

^2,0

^y

¹⁴⁰

^4,5

< ⁴⁰

⁴⁰ - ^{60 60} - ^{80 80} - ^{100 100} - ^{120 120} - ¹⁴⁰

^4,0

>

¹⁴⁰

^3,5

^3,0

^2,5

^2,0

^2,0

^4,0

^3,5

^3,0

^2,5

^{Tween 80}

Figure 12: Diagrammes de contours présentant les effets des différents facteurs sur l'activité

42