Introduction à la géométrie non-euclidienne

1.3. Les conséquences du cinquième postulat

Les conséquences du postulat des parallèles sont les suivantes dans la géométrie euclidienne :

a) Si deux droites (AB) et (CD) sont parallèles, toute droite (E'F') qui coupe l'une coupe l'autre.

Demonstration

Soit F le point commun à la droite (CD) et à la droite (E'F'): si la droite (E'F') ne coupait pas la droite (AB), elle lui serait parallèle, et par le point F passeraient deux droites (CD) et (E'F') parallèles à une même troisième (AB), ce qui n'est pas le cas. Donc, la droite (E'F'), coupe la droite (AB).

b) Deux droites (AB) et (CD) parallèles à une même troisième (E'F') sont parallèles entre elles.

Demonstration

Si la droite (CD) n'était pas parallèle à la droite (AB), elle la couperait : elle couperait aussi la droite (E'F') parallèle à la droite (AB), elle ne serait donc pas parallèle à (E'F').

Théorème 1.2.

Si deux droites parallèles sont coupées par une sécante :

a) Les angles alternes-internes sont égaux.

b) Les angles alternes-externes sont égaux.

c) Les angles correspondants sont égaux. Demonstration

Soient deux parallèles AB et CD et la sécante EF :

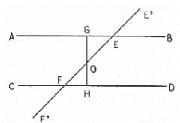
1°) Par le milieu O de EF menons la perpendiculaire GH à AB, qui est aussi perpendiculaire à
CD. Les triangles rectangles EOG et FOH ont un angle aigu égal à, et

l'hypoténuse égale, OF=OE. Ils sont égaux, et les angles et sont égaux.

2) Les angles alternes externes et sont égaux, car est opposée par le

sommet à l'angle , qui est alterne interne avec l'angle .

Réciproquement :

Si deux droites sont coupées par une sécante qui forme avec ces droites : - Soit deux angles alternes internes égaux,

- Soit deux angles alternes externes égaux,

- Soit deux angles correspondants égaux,

Alors ces deux droites sont parallèles.

Remarque 1.2.

Pour démontrer le parallélisme de deux droites, il faut et il suffit que les angles alternes internes, alternes externes ou correspondants, formés par ces deux droites avec une sécante, soient égaux.

1.4. Espaces vectoriels

Définition 1.2.

Etant donné un groupe commutatif E et K un corps commutatif, nous dirons que E est un espace vectoriel sur K s'il existe une multiplication externe associant à tout a?K et à tout

x?E, un élément de E noté a x, avec les propriétés suivantes :
- 1 x = x	(1.1.)
- a (? x) = (a /3) x	(1.2.)
- a (x+y) = a x + a y	(1.3.)
- (a + /3) x = a x + /i x	(1.4.)

Remarque 1.3

Les éléments de E sont appelés des vecteurs, et les éléments de K des scalaires.

Exemple 1.1

- Il est démontré que R est un espace vectoriel sur lui-même.

- Il est aussi démontré que Rⁿ est un espace vectoriel sur R.

Définition 1.3.

Une partie non vide F de l'espace vectoriel E sur K est un sous-espace vectoriel de E si elle vérifie les deux propriétés suivantes :

- (F, +) est un sous-groupe de (E, +) (1.5.)

- ? á ? K , ?x? F :áx? F (1.6.)

Remarques 1.4.

- Les opérations définies dans E sont donc également définies dans F et lui donnent une structure d'espace vectoriel sur K.

- Les conditions (1.5.) et (1.6.) peuvent s'écrire :

? ? ? ? ? ?

x F y F

, , á , á â

K x y F

+ ? (1.7.)

Définition 1.4.

Soit une suite (x1,..., x_n) de n éléments de E ; une combinaison linéaire de cette suite est un élément de la forme y = a1x1 + ... + anxn où a1,..., a_n sont des éléments quelconques de K. L'ensemble des combinaisons linéaires de la suite (x1,..., x_n) est appelé sous-espace vectoriel de E.

Définitions 1.5.

Une famille d'éléments de E est dite génératrice (de E) lorsque tout élément de E peut s'écrire comme une combinaison linéaire des éléments de cette famille.

Définitions 1.6.

On dit que la famille de vecteurs (x1,...,x_n ) de E est liée si l'on peut trouver des scalaires ct1,...,ct_n ? K, non tous nuls, tels que :

a1x1 + a2x2 +...+ Ánxn = 0 (1.8.)

Remarque 1.5.

On dit aussi dans ce cas que les vecteurs de la famille sont linéairement dépendants. Définitions 1.7.

La famille de vecteurs (x1,...,x_n )de E est dite libre lorsqu'elle n'est pas liée ; c'est-àdire que x1,...,x_n sont libres ou linéairement indépendants ; ceci signifie que l'égalité (9) entraîne :

cL1 = cL2 = ... = cL_n=0. (1.9.)

Remarque 1.6.

On peut montrer qu'une famille (x1, x2) de deux vecteurs de E est liée si et seulement s'il existe un scalaire cL tel que x2 = a x1 ou un scalaire f3 tel que x1 = fix2. On dit dans ce cas que les deux vecteurs sont colinéaires. En revanche, rien n'assure qu'une famille liée comportant plus de trois vecteurs contienne forcément deux vecteurs colinéaires.

Définitions 1.8.

On appelle base de l'espace vectoriel E toute famille d'éléments de E libre et génératrice. On peut montrer qu'une famille d'éléments de E est une base si et seulement si tout élément x de E s'exprime de manière unique comme combinaison linéaire des éléments de .

Remarque 1.7.

Si un espace vectoriel E admet une base ayant un nombre fini de n éléments, alors toute base de E est composée de n éléments.

Définition 1.9.

On appelle dimension d'un espace vectoriel E, notée dim E, le nombre d'élément n de sa base.

Remarques 1.8.

(1) Un espace vectoriel réduit à {0} n'a pas de base. Il est de dimension finie et on pose dim E = 0.

(2) Un espace vectoriel E est de dimension finie si et seulement s'il admet une famille génératrice ayant un nombre fini d'éléments.

(3) Les espaces vectoriels qui ne sont pas de dimension finie sont dits de dimension infinie. Pour qu'un espace vectoriel E soit de dimension infinie, il faut et il suffit qu'il existe une famille libre infinie d'éléments de E.

Définition 1.10.

On appelle droite vectorielle tout espace vectoriel de dimension finie égale à 1 et plan vectoriel tout espace vectoriel de dimension finie égale à 2.

Remarques 1.9.

(1) Soit E un espace vectoriel de dimension finie. Alors :

tout sous-espace vectoriel F de E est de dimension finie, et dim F < dim E

si F est un sous-espace vectoriel de E tel que dim F = dim E, alors F = E.

(2) Soient E un espace vectoriel de dimension finie, et F1, F2 deux sous-espaces vectoriels de E. Alors :

dim (F1 + F2) + dim (F1 fl F2) = dim F1 +dim F2