Modélisation en risques de crédit : dérivés de crédit et calibration de modèles structurels

Chapitre 4 Les modèles structurels

Par suite, si l'on connait ót et Et, on connaît, en principe, la valeur des variables At et óA. Il suffit pour cela de résoudre en At et ó le système suivant :

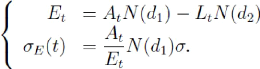
Et = AtN(d1) LtN(d2) óE(t) =(At / Et )* N(d1)ó

La relation (4.3) n'ayant lieu qu'instantanément les résultats obtenus par cette méthode risque d'être instables .

4.2.7 Spread implicite et smile de volatilité

Nous preesentons maintenant une nouvelle meethode pour implémenter le modele de Merton, d'apres Hull, Nelken et White .Il s'agit d'utiliser l'information contenue dans le smile de volatilité implicite pour calibrer le modèle de Merton et en particulier estimer le spread implicite.

Cette implémentation permet de classer les emetteurs de dette risquete selon la qualité de leur signature. L'intérêt d'un tel classement est important : d'une part, il permet de comparer le risque de crédit entre plusieurs firmes et d'autre part, il peut servir de base à une estimation des probabilités de defaut à horizon donné. Enfin, ce modèle permet de relier risque equity et risque de crédit.

Dans le modèle de Merton, un put de maturité ô < T et de strike K apparaît comme une option composee sur la valeur de l'entreprise. Ainsi, la valeur du put sur l'action est donnée par la formule suivante :

Avec :	,

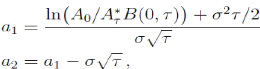
Où M désigne la fonction de répartition d'une gaussienne bivariée :

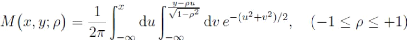
et A*ô représente la valeur de la firme telle qu' à l'instant ô, l'on ait