Chapitre 4 Les modèles structurels
Autrement dit, A*ô est la valeur en dessous de laquelle le
put sur l'action sera exercé. Notons í la volatilité
implicite du put et posons
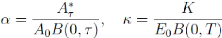
Le paramètre ? est souvent
appelé moneyness de l'option (lorsque ? = 1, l'option
est à la monnaie du forward). Le paramètre á est
la moneyness du point de vue de la valeur de la firme. Par définition,
la volatilité implicite y du put est solution de
l'équation
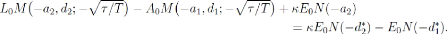
Où
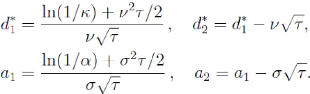
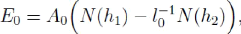
En utilisant alors l'équation
(4.4)
il vient
(5.5)
|
En
|
|
utilisant une nouvelle fois l'équation (4.4), nous
pouvons aussi écrire que
|
Chapitre 4 Les modèles structurels
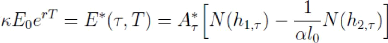
Où
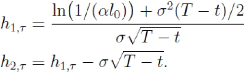
de sorte que (4.6)
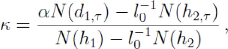
Pour un jeu de paramètres (l0; ó;
T) du modèle de Merton et une maturité d'option ô
(< T), les équations (4.5) et (4.6) définissent
une relation implicite de la forme y = Fonction(?);qui conduit à un
smile de volatilité. Les propriétés de cette relation
peuvent se résumer en quelques faits stylisés :
(1) le spread de crédit est une fonction croissante de la
volatilité implicite ;
(2) la relation entre la pente (skew) du smile de
volatilité et le spread de crédit est plus complexe : pour des
spreads faibles, la pente est une fonction croissante du spread ; pour des
niveaux de spread plus élevés, la variation de la pente devient
négligeable ;
(3) enfin, la pente est une fonction croissante de la
volatilité implicite à la monnaie.
Ces résultats suggèrent une nouvelle
méthode pour implémenter le modèle de Merton :
étant données deux volatilités implicites et une valeur
pour T, on peut résoudre les équations (4.5) et (4.6)
pour obtenir l0 et ó. Cette implémentation
permet donc d'estimer directement le spread de crédit et la
probabilité risque-neutre de défaut à partir du smile de
volatilité tout en évitant le recours à la relation
instantanée (4.3).
Ces résultats peuvent ensuite être
utilisés comme un indicateur du risque de crédit. Les auteurs ont
testé cette approche en comparant le classement des spreads obtenus par
cette méthode avec les spreads du marche des CDS et ont montré
que ces classements sont proches. Cette méthode permet donc, par
exemple, d'étudier la qualité de la signature d'entreprises dont
le marché de CDS n'existe pas ou n'est pas très liquide.
Chapitre 4 Les modèles structurels
4.2.8Limites du modèle et extensions
La principale limitation du modèle de Merton est que
les spreads implicites court terme sont nécessairement proches de
zéro contrairement aux spreads réellement observés sur les
marchés de capitaux. Cette propriété du modèle est
liée à la continuité de la filtration brownienne (ou, de
manière équivalente, à la prévisibilité de
l'instant de défaut). Duffie et Lando expliquent cette apparente
contradiction par le fait que l'asymétrie d'information qui existe
entre les actionnaires et les détenteurs de la dette n'est pas prise en
compte par ce modèle. Ils ont montré [10] que si ces derniers
ne disposent que d'une information comptable partielle (ou
«bruitée») l'instant de défaut leur apparait comme
totalement inaccessible. Ces résultats permettent de justifier
l'utilisation des modèles à forme réduite dont nous
aborderons l'étude dans le prochain chapitre.
Le modèle de Merton peut être étendu dans
différentes directions : Nous verrons dans la section 4.3
consacrée aux modèles de premier instant de passage comment l'on
peut incorporer des défauts se produisant à un instant quelconque
de l'intervalle [0; T] ; Vasicek [11] propose un modèle de
Merton prenant en compte l''echelonnement de la dette ; Longstaff &
Schwartz [12] introduisent un modèle de Merton intégrant des taux
stochastiques.
Notons enfin que si l'on souhaite tenir compte des
imperfections de marché (telle l'incomplétude ou le
contrôle que peuvent exercer actionnaires et détenteurs de la
dette sur la conduite de l'entreprise), la théorie s'éloigne
sensiblement de la théorie des options. Sur ce sujet, l'on pourra se
référer à Leland [13].
4.3 Modèles de premier instant de passage
L'une des limites du modèle de Merton réside
dans le fait que le défaut de l'émetteur ne peut intervenir qu'
à la maturité de la dette. Dans les modèles de premier
instant de passage, au contraire, l'instant de défaut est (un temps
d'arrêt) de la forme ô = inf{t > 0 ; At
< Bar(t)} où Bar est une barrière qui
peut être aléatoire et A est une variable de type
«valeur de la firme». Dans les modèles de ce type, il est
possible de spécifier une grande variété
d'hypothèses de recouvrement en cas de défaut .
Apres quelques préliminaires mathématiques, nous
présenterons un exemple de modèle de premier instant de passage :
le modèle Credit Grade développé par JP
Morgan.
Chapitre 4 Les modèles structurels
| 


