4.3.1 Préliminaires mathématiques
Nous commençons ce paragraphe par un lemme bien connu de
la théorie des diffusions Dans la suite, Y désigne un
mouvement brownien avec dérive de sorte que
Yt = y0 + pt + óBt ;
(y0 > 0; p ? IR; ó > 0)
où B est un mouvement brownien unidimensionnel.
4.3.2 Lemme
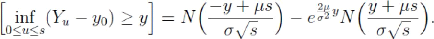
Une preuve de ce lemme est donnée en Annexe
Considérons le temps d'arrêt v = inf{t
> 0 ; Yt < 0 }.Appliquer le lemme précédent
à Yy0 suffit à prouver :
4.3.3 Proposition La variable aléatoire ô est
distribué selon la loi gaussienne inverse. Plus
précisément,
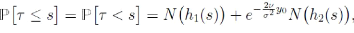
où
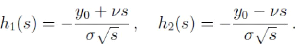
Exemple. Nous considérons une entreprise dont la valeur
A est décrite comme dans le modèle de Merton et nous
supposons que l'instant de défaut de la firme se présente sous la
forme v = inf{t > 0 ; At < v } où v
est un réel inferieur `a A.
Dans ce cas, nous avons :
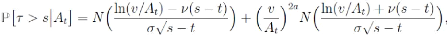
Ou
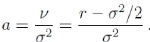
Chapitre 4 Les modèles structurels
4.4 Modèle Credit Grade
Dans ce paragraphe, nous présentons un modèle de
premier instant de passage développé par JP Morgan (Credit
Grade, voir [14]).
Nous avons choisi de présenter ce modèle car il
nous semble qu'il contient des intuitions puissantes sur ce que sont les
déterminants du risque de défaut et les liens qui existent entre
le risque de crédit et le risque equity.
4.4.1 Description du modèle
Nous supposons que la «valeur» V d'une
entreprise est décrite par un processus satisfaisant à l'EDS
dVt / Vt = ó dWt ;
(ó > 0);où W est un mouvement
brownien unidimensionnel et ó > 0 est la
volatilité de V.
Ici, V n'est pas réellement la valeur de la
firme mais plutôt un indice mesurant l'évolution temporelle de la
qualité du crédit de l'entreprise. Dans ce modèle, le
défaut est défini comme le premier instant ou V atteint
une barrière LD où
(1) D est le ratio debt-per-share,
(2) L est une grandeur aléatoire
représentant le taux de recouvrement moyen global en cas de
défaut.
La variable L est supposée log normale de moyenne
L et d'écart-type de sorte que LD =
LDexp (AZA
2/2 ) où
Z suit une loi normale centrée réduite.
La moyenne L et l'écart-type ë sont
estimés historiquement en utilisant des données de taux de
recouvrement telles celles fournies par Standard & Poor's. Dans [14], les
auteurs mentionnent les valeurs L = 0,5 et ë =
0,3 obtenues à partir des données de défaut de
300 entreprises américaines (hors institutions financières) entre
1987 et 1997.
Le ratio debt-per-share D est obtenu en divisant le
nominal de la dette globale par le nombre d'actions émises par
l'entreprise. Pour une valeur V0 donnée, l'instant ô
de défaut est donc
r = inf{t > 0 ; Vt <
LD}
et si l'on pose Xt = óWt -ëZ-
1/2ó 2 t-1/2ë2
Xt ~ N(-Y2 At 2, At ),o`u
At 2= ó 2 t +
ë2, cette formule peut se réécrire r
= inf{t > 0 ; Xt < ln (LD/V0) -
ë2}
Pour appliquer les formules présentées dans le
paragraphe précédent (afin d'obtenir une formule fermée
pour la structure par terme de probabilité de défaut), les
auteurs proposent de remplacer Xt avec un mouvement brownien Yt
de loi N(ìt; è2t),
où è2t = At2 =
ó 2t + ë2 et
ìt =-Y2 At 2, D'après
le lemme 4.3.2, l'on a
Chapitre 4 Les modèles structurels
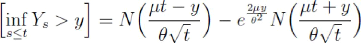
et en posant y = ln(LD/V0)- ë2,
l'on obtient la formule :
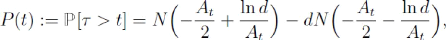
Où
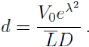
Remarque. L'introduction dans un
modèle structurel d'une barrière aléatoire implique que la
probabilité de défaut instantanée n'est plus nulle. Ceci
conduit à un spread court-terme non nul et permet de résoudre
l'un des problèmes inhérents aux modèles à la
Merton.
| 


