4.4.2 Probabilité de défaut et spread de
crédit
Dans ce paragraphe, nous désignons par spread de
crédit la valeur de la marge d'un Credit Default Swap qui annule sa
valeur au moment de l'entrée dans le swap. Autrement dit, le spread est
donné par la formule
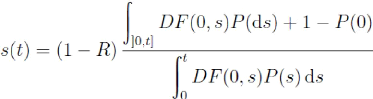
Il faut bien prendre garde au fait que R est le taux
de recouvrement spécifique au titre couvert par le CDS et n'est donc pas
nécessairement égal à L qui est un taux de
recouvrement moyen global. Typiquement, le taux de recouvrement pour une
dette unsecured sera plus faible que L, alors que celui
lié à une dette secured sera plus grand que
L.
Remarque.
Si l'on note
p(t) = -1/t . ln
P(t);
le taux de défaut moyen et si l'on suppose que
(1) p(t) p constant,
(2) P(0) 1,
alors l'approximation suivante est justifiée
s(t) (1-R)p.
Chapitre 4 Les modèles structurels
4.4.3 Calibration du modèle sur les données
de marche
Nous cherchons maintenant à calibrer ce modèle
sur des données de marché observables(données equity).
Soient S et óS respectivement la valeur de l'action et
la volatilité de l'action de l'entreprise considérée. La
méthode proposée par JP Morgan consiste à examiner les
conditions aux bords à long terme sur une expression de type
distance-au-défaut pour les deux régimes extrêmes
§ prés du défaut c'est- à-dire
S--0,
§ loin de la barrière c'est-à-dire S
LD.
Soit donc ç la distance-au-défaut mesuré en
écart-type de V et définie par
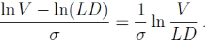
Reprendre le raisonnement qui nous a conduit à la formule
4.3 permet d'exprimer la distance-au-défaut sous la forme :
(4.7)
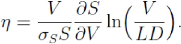
Nous allons établir les conditions aux bords pour.
Prés du défaut (S--0), nous
Avons
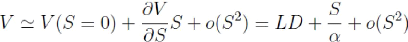
En utilisant l''equation précédente et (4.7), on
montre que lorsque S--0
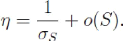
Lorsque S »LD, on suppose que S/V--1 (ce
qui est cohérent avec le comportement d'un modèle de Merton
standard). Par suite,
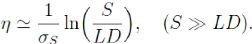
L'expression la plus simple pour qui satisfasse
simultanément à ces deux conditions aux bords est
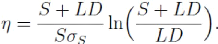
En comparant l'équation précédente avec
(4.7) nous sommes conduits à
Chapitre 4 Les modèles structurels
V = S + LD ; et donc V0 =
S0 + LD:
Finalement, l'on obtient
ó= ó*S . {S*/(S* +
LD)}
pour une valeur de l'action égale à S et
sa volatilité (historique ou implicite) correspondante.
La formule suivante pour la probabilité (risque neutre) de
défaut ne fait plus intervenir que des variables observables
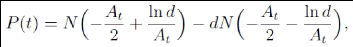
Où
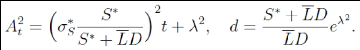
| 


