Modélisation en risques de crédit : dérivés de crédit et calibration de modèles structurels

Chapitre 5 Les modèles structurels en pratique

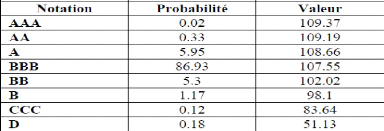
Valeur d'un titre BBB

Ces résultats sont traités sur une feuille Excel comme suivant :

^categorie

^AAA

^AA

^A

^BBB

^BB

^B

^CCC

^AAA

^90,81%

^8,33%

^0,68%

^0,06%

^0,12%

^0,00%

^0,00%

^0,00%

??

^AA

^0,70%

^90,65%

^7,79%

^0,64%

^0,06%

^0,14%

^0,02%

^0,00%

^A ^BBB

^0,09% ^2,27% ^0,02% ^0,33%

^91,05% ^5,95%

^5,52% ^0,74% ^86,93% ^5,30%

^0,26% ^1,17%

^0,01% ^0,06% ^0,12% ^0,18%

^BB

^0,02% ^0,14%

^0,67%

^7,73% ^80,53%

^8,84%

^1,00% ^1,06%

^B

^0,00% ^0,11%

^0,24%

^0,43% ^6,48%

^83,46%

^4,08% ^5,20%

^CCC

^0,22% ^0,00%

^0,22%

^1,30% ^2,38%

^11,24%

^64,85% ^19,79%

^DEFAULT categorie

^0,00% ^0,00% ^Année 1

^0,00%Année 2

^0,00% ^0,00% Année 3 ^5,25

^0,00% Année 4 ^5,63

^0,00% ^100,00%

^AAA

^3,6

^4,17

^4,73

^5,12

^AA

^3,65

^4,22

^4,78

^A

^3,72

^4,32

^4,93

^BBB

^4,1

^4,67

^BB

^5,55

^6,02 ^6,78

^DEFAULT

^5,17

^5,32

^7,27

^B

^6,05

^7,02

^8,03

^8,52

^CCC

^15,5

^15,02

^14,03

^13,52

^{Tableau des taux forward (taux sans risque} + ^{prime de risque)}

A partir du tableau des différentes valeurs de BBB selon sa migration, on peut déduire la distribution des variations de prix de l'obligation, comme le montre l'exemple suivant :

En s'aidant d'une feuille Excel, on obtient les résultats suivants ;

Chapitre 5 Les modèles structurels en pratique

^SOURCE :

^{DISTRIBUTION OF THE BOND VALUES AND CHANGES IN VALUE OF BBB BOND,IN 1 YEAR}

^{year-end rating}

^{pobability of state:p%}

^{forward price:V($)}

^AAA

^0.02

^AA

^0.33

^A

^5.95

^BBB

^86.93

^BB

^5.3

^B

^1.17

^CCC

^0.12

^D

^0.18

^{CreditMetrics de JPMorgan}

Year-endthe end of a financial year or calendar year

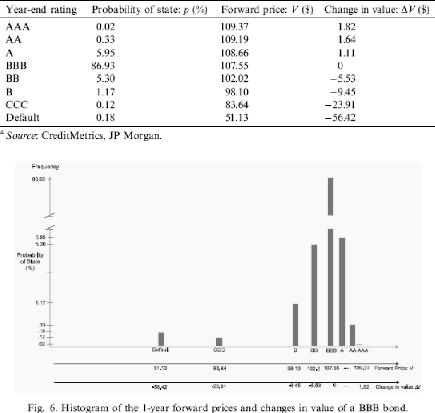
^{change in value:Äv($)}

^1,8190561

^1,641426998

^1,112048194

⁰

^-5,524558376

^-9,445030719

^-23,92547137

^-56,4009439

On voit que la distribution n'est pas normale car non symétrique. La distribution ci-dessus est

Chapitre 5 Les modèles structurels en pratique

obtenue en mettant en abscisse les différentes valeurs de variation du prix du titre (seul titre présent dans le portefeuille) et en ordonnée, les probabilités de migration.

La CreditVaR à 1% (c'est-à-dire perte maximale attendue pour une probabilité de 1%) ou en d'autres termes pour un niveau de confiance de 99% est obtenue en prenant le premier percentile de la distribution des variations de prix de l'obligation, soit CreditVaR = -23,91.

On prend 1% de l'aire de la distribution ci-dessus en partant de la gauche car les valeurs de variation du prix du titre sont rangées dans un ordre ascendant (des nombres négatifs = pertes vers les nombres positifs = gains).

5.1 .2.2 Principe du modèle : portefeuille à deux obligations

Dans le cas de plusieurs actifs dans le portefeuille, la migration des différents crédits est corrélée (les valeurs des titres d'un même secteur d'activité ou d'une même région géographique sont en principe fortement corrélées). Il est alors nécessaire d'estimer ces corrélations. Le problème est qu'il n'y a pas de bonnes données observables. Par conséquent,

pour le calcul des corrélations entre migrations des crédits, CreditMetrics utilise les corrélations entre les valeurs des actifs des émetteurs des crédits qui sont approchées par les

corrélations entre les prix des actions de ces émetteurs (il est possible d'utiliser aussi les

obligations mais leur historique est moins important que celui des actions).

Cependant, pour pouvoir dériver les corrélations des migrations des crédits des corrélations des valeurs des actifs, il faut disposer d'un modèle liant la qualité d'un crédit à la valeur des actifs. Le modèle utilisé est une extension du modèle de Merton (1974) qui incorpore les migrations des crédits.

Dans le cadre de ce modèle, en considérant les probabilités de migration d'une entité initialement notée BB qui sont données par le tableau de Standard & Poor's suivant :

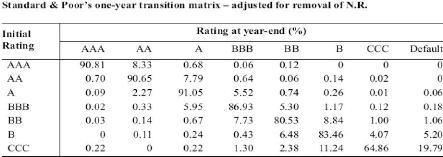
On suppose que le comportement du rendement d'un titre est modélisé par : r = u+o€où €~>N(0,1). La probabilité de défaut d'un émetteur du titre est donnée par : Pr{défaut} = Pr{ r < ZDef } = Pr{ u+o€< ZDef } = Pr{ o€< ZDef } si on suppose u= 0. D'où Pr{défaut} = Pr{ € < ZDef /o} = cJ(ZDef /o) où cJ est la fonction cumulative de la loi normale.

où 1-4(ZAA/o) désigne la probabilité pour l'entité BB de passer à la notation AAA, ZAA représentant le seuil à partir duquel l'entité BB passe à AAA.

Chapitre 5 Les modèles structurels en pratique

Graphiquement, les données du tableau apparaissent de la façon suivante (si on suppose que les rendements des actifs de l'entité BB suivent une loi normale)

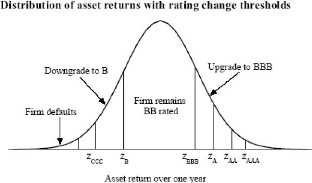
Sachant que Zdef = cb-1(1.06%).a = -2.30 a, nous obtenons la valeur de chacun des seuils ZAAA, ZAA, ZA, ... en fonction de a qui correspond à l'écart-type de la distribution normale des rendements des actifs de l'entité BB :

Z BBB ZAA

On a P(Z B B G r = Z BBB, ZAA = r' = ZAAA) = f f f(r,r',a,a') drdr'

Z B B ZA

Comme on a cb(Zdef /a)=1.06% alors on a Zdef /a = cb-1(1.06%)4 Zdef = a cb-1(1.06%)

On utilisant la fonction NORMSINV function (normal standard inverse) d'un tableau Excell,on obtient Zdef = a cb-1(1.06%)=-2,3044 a ; avec cb-1 : NORMSINV

De même, et toujours d'après le tableau précédent on a aussi:

cb(ZCCC /a)- cb(Zdef /a)= 1% 4 cb(ZCCC /a)= cb(Zdef /a)+ 1%

4 ZCCC /a = cb-1 (cb(Zdef /a)+ 1%)

4 ZCCC = a cb-1 (cb(Zdef /a)+ 1%)

=a cb-1 (1.06% + 1%)

= a cb-1 (2.06%)

= -2,0415 a

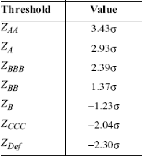
On refait le même raisonnement de calcul pour déterminer les autres seuils ZB, ZBB, ZBBB, ZA, ZAA et

on obtient le tableau suivant :

Chapitre 5 Les modèles structurels en pratique

^ZAA
^SEUIL
^ZA
^ZBBB

^ZCCC	^2,04a
^Zdef
	^VOCAB
^EN		^FR
^thresholds		^seuil
^value
^asset
^according to
^over
^remains

Chapitre 5 Les modèles structurels en pratique

Supposons que nous ayons un second émetteur noté A et dont les rendements des actifs

suivent une loi normale avec un paramètre a', nous obtenons alors le tableau suivant (construit de la même façon que pour BB) :

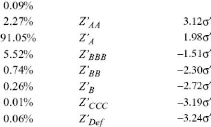
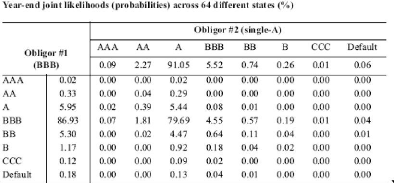
Disposant de ces deux tableaux d'informations pour les 2 entités notées BB et A, nous pouvons calculer les probabilités de migration jointes de la façon suivante :

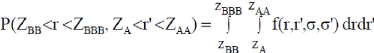
où r et r' représentent respectivement les rendements des actifs de BB et de A et f(r,r',a,a') désigne la fonction de densité jointe de la loi gaussienne qui dépend du coefficient de corrélation p. La fonction de densité jointe de la loi gaussienne des variables X et Y se

présente comme suit (la moyenne de X et Y est supposée nulle) :
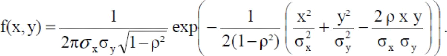