ANNEXE 1
Le lemme d'Itô, ou encore
formule d'Itô est l'un des principaux résultats
de la théorie du calcul stochastique. Ce lemme offre un moyen de
manipuler le mouvement brownien ou les solutions d'équations
différentielles stochastiques (EDS).
Énoncé
Soit un processus d'Itô processus stochastique de
la forme
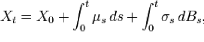
Autrement formulé, on a
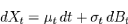
avec et deux fonctions aléatoires satisfaisant quelques
hypothèses techniques d'adaptation au
processus (mouvement brownien).
Si est une fonction de classe alors la formule
d'Itô s'écrit
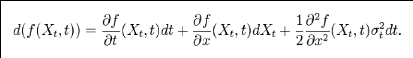
Un exemple : le modèle Black-Scholes
Le mouvement brownien géométrique est
souvent utilisé en finance comme le plus simple modèle
d'évolution de cours de bourse. Il s'agit de la solution de
l'équation différentielle stochastique :
où
? est le prix de l'action sous-jacente,
? (constant) est le taux de dérive jen)
du prix de l'action,
ANNEXE 1
? (constante) est la volatilité du prix de
l'action,
? est un mouvement brownien.
Si alors nous sommes face à une équation
différentielle ordinaire dont la solution est
En posant on obtient grâce à la formule
d'Itô :
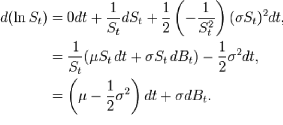
On peut alors intégrer et il en découle que :
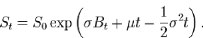
Applications
? La formule d'Itô est l'une des pierres angulaires du
calcul stochastique, et est utilisée dans de
très nombreux domaines: mathématiques
appliquées, physique, finance, biologie, Mécanique
quantique, traitement du signal, etc..
En calcul stochastique,
? Elle permet de faire le lien entre les solutions d'EDS et des
opérateurs différentiels du
second ordre, et donc entre la théorie des
probabilités et celle des équations aux
dérivées partielles.
? Elle permet d'affirmer l'existence de solutions d'EDS sous des
conditions (très) faibles de
régularité sur les coefficients.
ANNEXE 2
Equation de Black & Scholes (modèle
standard)
Nous allons étudier ici le modèle BS dans sa forme
simple avant l'apport de Robert Merton sur la volatilité
déterministe et les taux aléatoires.
Considérons un marché sans coût de
transaction où sont échangés 2 types d'actifs avec absence
de possibilité d'arbitrage: risqué et non risqué. La
cotation est réalisée en continue à un taux constant
r. Le spot du sous-jacent à l'émission est noté
S0 et son évolution est déterminée par un mouvement
brownien. On notera p la tendance ou dérive (i.e.
l'espérance de rentabilité du support sur son historique de
cours), ó la volatilité du sous-jacent (le paramètre de
diffusion) et Wt un mouvement brownien.
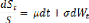
Cette équation est donc une équation
différentielle stochastique (EDS) qui régit un mouvement brownien
géométrique (MBG) St avec p et ó connues
et constants. On peut déduire la dérive du mouvement :
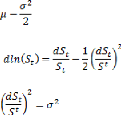
Car d'après le lemme d'Itô on obtient pour
ln(St) :
Ce qui nous permet d'écrire :
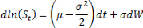
On retrouve donc bien le terme de dérive du mouvement. On
peut également montrer que ce MBG est log-normalement distribué
en rappelant que S0 ne peut être négatif car le cours d'une action
n'est jamais négatif en vertu de la responsabilité limité
de l'actionnaire:
St est donc log-normal et la solution de St s'écrit :
| 


