ANNEXE2
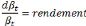
|
|
|
Définissons à présent la valeur ât de
l'actif sans risque en t.
|
On peut définir le rendement de l'actif
|
sans risque au taux constant r comme la
différentielle de ât : La solution de cette
équation est :
Introduisons à présent une option européenne
avec pour sous-jacent St. Notons qu'aucun dividende n'est versé.
L'intuition de F. Black et M. Scholes s'exprime par la recherche
dans les stratégies autofinançantes de celle(s) qui duplique(nt)
le call et dont la ou les valeur(s) s'exprime(nt) comme une fonction
déterministe de St et de t que l'on notera it(t, St). L'idée est
donc qu'il existe un portefeuille autofinancé composé du
sous-jacent et de l'actif sans risque dont la valeur en T est égale au
payoff ØT de l'option. On tente donc de trouver le processus itt qui
représente la valeur d'un portefeuille autofinançant et dont la
valeur en T est celle du payoff à dupliquer. L'expression it doit donc
être suffisamment régulière au sens d'Itô ;
i.e. la fonction it doit être 1 fois continûment
différentiable sur t et 2 fois continûment différentiable
sur St. Sous ces conditions, nous pouvons appliquer la formule d'Itô :
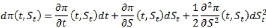
De notre 1ère équation
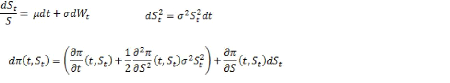
on déduit et on remplace :
On cherche à présent à respecter
l'égalité suivante ()
Afin que it(t, St) représente à tout instant t la
valeur d'un tel portefeuille. Remanions cette égalité :
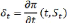
ANNEXE2
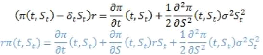
On a ainsi obtenu l'équation aux
dérivées partielles de Black &
Scholes (EDP d'évaluation). A ce stade il reste à
vérifier que le portefeuille autofinançant synthétise
l'option :
Rappelons que nous sommes en absence de possibilité
d'arbitrage, ce qui implique que la valeur du portefeuille dupliquant est,
à chaque instant, égale à celle du titre dupliqué
:
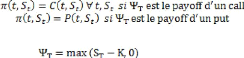
Dans le cas où le payoff est égal à celui
- d'un call ( )
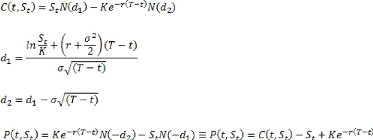
- ou d'un put ( ) ,la solution est donnée par la formule
de Black & Scholes :
,
Notons que N(u) fait référence à la
fonction de répartition de la loi normale centrée
réduite :
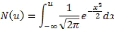
ANNEXE 3
|
Démonstration du Lemme 4.3.2
|
Dans cette partie, nous allons démontrer le
résultat suivant :
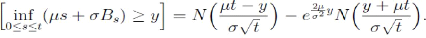
Posons
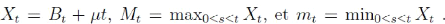
La démonstration revient à prouver le lemme suivant
: Lemme E.1
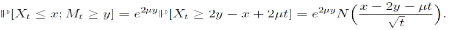
En
effet :
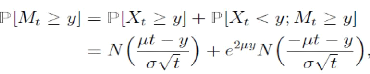
et donc
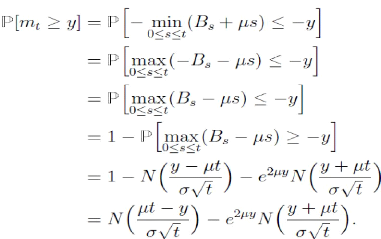
ANNEXE3
L'extension au cas général est alors
immédiate en écrivant :
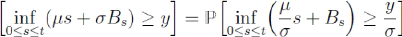
La démonstration du lemme 4.3.2 repose sur le Principe
de réflexion dont nous rappelons l'énoncée :
Proposition E.2 (principe de réflexion) Parmi les
trajectoires browniennes qui atteignent le niveau y avant l'instant t, il y en
a autant en dessous de x qu'au dessus de 2y-x en t. Autrement dit
:
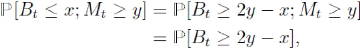
ce qui se réécrit de la façon suivante
:
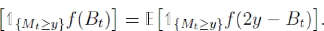
Nous allons à présent prouver le lemme.
D'âpres le théorème de Girsanov il existe une
probabilité'e P 'équivalente à P définie par sa
densité de Radon-Nikodym
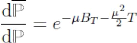
Telle que
Soit un -mouvement brownien, et une probabilité
équivalente à
définie par la densité
|
Telle que Wt = Xt + ìt soit un
e -mouvement brownien.
|
|
Soit x=y, on a
|
| 


