2.2 Enjeux
Le risque de crédit peut être défini, en
première approximation, comme le risque de perte lié au
changement de la qualité de la signature d'une contrepartie. Toutes les
institutions
Chapitre 2 Outils et concepts de base pour modéliser le
risque de crédit
financières (ainsi que tout les acteurs du marché)
accumulent une grande quantité de risque de crédit: soit
directement par l'intermédiaire de leurs portefeuilles de
créances, soit indirectement sous la forme de risques de contrepartie
dans leurs portefeuilles d'actifs et de produits dérivés OTC.
L'enjeu que représente la modélisation de ce risque est donc
très important : il s'agit de pouvoir : -- mesurer le risque de
crédit contenu dans les portefeuilles,
-- évaluer les instruments financiers sensibles au
risque de crédit et, plus généralement, tout instrument
exposé à ce risque (risque de contrepartie), et ce à un
niveau agrégé. Il est, en effet, important de pouvoir
contrôler l'exposition au risque de crédit contrepartie par
contrepartie ainsi que l''evolution de cette exposition par secteurs
géographiques et industriels. De telles pratiques permettent, par
exemple, de réduire le risque de concentration.
La production de résultats quantitatifs robustes permet
alors à l'institution concernée
-- d'allouer à chaque centre de profit un capital
économique adéquat,
-- d''evaluer la performance des centres de profit au regard des
risques pris,
-- de fournir des informations fiables sur son
intégrité financière aux régulateurs, aux
investisseurs et aux agences de notation,
-- de diversifier et réduire le risque en imposant, par
exemple, des limites à l'exposition au risque de crédit par
contrepartie.
La mise en place de tels processus de gestion du risque
correspond à l'évolution de la réglementation prudentielle
et aux trois piliers du nouvel accord de Bale .
2.3 Modèles du risque de crédit
Dans cette section, nous exposons les approches classiques de la
modélisation du risque de défaut à partir de
l'étude du concept central d'obligation zéro-coupon
risquée (C'est-à-dire soumise au risque de défaut). Il
existe deux grandes familles de modèles d'évaluation de la dette
risquée : -- les modèles structurels,
-- les modèles à forme réduite.
Nous mentionnons aussi les modèles de
corrélation d'instants de défaut qui sont nécessaires
à l''evaluation des produits dérivés exotiques de
crédit ainsi que les modèles dit hybrides dont le but est de
permettre l''evaluation précise du risque de contrepartie des
portefeuilles de produits dérivés OTC.
Dans la suite, nous nous plaçons dans le cadre de
l''evaluation risque-neutre des actifs financiers :
nous supposons donnés un espace probabilisé
filtré sur lequel est défini le
processus des taux d'intérêt instantanés
(rt)t=0 et une probabilité risque-neutre P*.
Rappelons qu'alors la valeur des actifs contingent
(c'est-à-dire dont la valeur est contingente à l'évolution
des conditions de marché) est calculée comme l'espérance
sous cette probabilité de ses flux futurs actualisés au taux sans
risque. Une obligation zéro coupon (sans risque) est un actif qui paye 1
à sa maturité T.
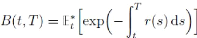
La valeur B(t; T) de cet actif est :
Chapitre 2 Outils et concepts de base pour modéliser le
risque de crédit
Si le risque de contrepartie de l'émetteur du
zéro-coupon n'est pas nul, l'évaluation du zéro-coupon
doit tenir compte de la possibilité du défaut de celui-ci : deux
nouveaux risques entrent en jeu -- l'instant du défaut,
-- la perte en cas de défaut (Loss Given
Default).
La perte en cas de défaut s'exprime en termes d'un taux de
recouvrement #177; éventuellement
aléatoire et d'une hypothèse de recouvrement.
Noter que ces hypothèses de recouvrement, que nous présentons
maintenant, s'étendent immédiatement à d'autres actifs que
les zéro -coupons risqués. Nous notons D(t; T)
la valeur en t du zéro -coupon risqué de maturité
T et ô l'instant du défaut de l'émetteur de ce
titre.
L'hypothèse de recouvrement la plus courante
s'appelle fractional recovery of par value et consiste en le
recouvrement à l'instant du défaut d'une fraction #177;
du nominal du titre. Dans ce cas, on a
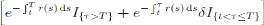
Si, en cas de défaut, la fraction recouvrée l'est
à maturité, on parle de fractional recovery of Treasury
value. Dans ce cas, on a
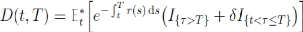
Une autre hypothèse classique dite fractional
recovery of market value suppose qu'à l'instant de défaut le
propriétaire du titre perçoit une portion #177; de la
valeur précédent immédiatement le défaut. Dans ce
cas
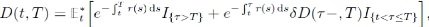
où D(ô-,T) (Si f est une fonction
à valeurs réelles, nous notons f (t-) la limite
lims?t;s<t f(s).) est la valeur avant défaut de
l'instrument considéré.
| 


