Marche aléatoire,mouvement brownien et applications

1.1.4 Martingales en temps continu

Les martingales continues sont l'analogue des martingales discrètes mais à temps continu, il s'agit d'un processus stochastique dont l'espérance à l'instant t dépend de l'information disponible à un certain temps s = t .

Définition 1.1.9. Un processus stochastique (M(t))t~0 à valeurs réelles, Ft-adapté et intégrable est une martingale continue si

E(M(t)/F_s) = M(s),s = t

Sous-martingale si

E(M(t)/F_s) = M(s)

Sur-martingale si

E(M(t)/F_s) = M(s)

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

1.2 Marche aléatoire

1.2.1 Marche aléatoire sur Z

Définition 1.2.1. Soit (Mn)n>0 une suite de variables aléatoires indépendantes et identiquement distribuées toutes à valeurs dans {-1,1} avec :

P{M_n = 1} = p et P{M_n = -1} = 1-p = q

On pose :

S0 = 0

{

_Sn =

_Xn i=1

Mi

La suite (Sn)n>0 est appelée marche aléatoire sur Z.

La marche aléatoire simple est dite symétrique lorsque p = q = 21

Pour la suite on concentre sur la marche aléatoire symétrique.

Proposition 2.
· E(S_n) = 0

· V (S_n) = n

On a

Puisque

E(Sn) =

n i=1

E(Mi) = 0

E(M1) = E(M2) = ... = E(M_n) = 0

Par calcul on trouve :

E(S^2n) =

Xn i=1

Xn j=1

E(MiMj) = 0

Puisque

E(MiMj) =

{

1 sii=j E(Mi)E(Mj) = 0 si i j

11

Définition 1.2.2. (Chemin) Soit n > 0 ,m > 0 et a,b E Z on appellera chemin du point (m,a) au point (n,b) une ligne brisée, c'est-à-dire une suite de segments joignant des points successifs du plan (m0,a0),(m1,a1),
·
·
· ,(m_r,a_r), qui commence au point (m0,a0) = (m,a) et se termine au point (m_r,a_r) = (n,b).

Notation : On note un chemin pour une marche aléatoire de n pas par (S0,S1,
·
·
· ,S_n) E Zⁿ+¹. Pour la suite nous nous concentrons surtout sur les chemins qui joignent ((m,a) = (0,0) au point (n,b) = (n,S_n).

Notons nd : le nombre de fois où Mi = +1 et n_g : le nombre de fois où Mi = -1

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

12

alors

{ n = nd +ng sn = nd - ng

donc

{ nd = 2 n+sn n--sn ng = 2

La position S_n = s_n est donnée par

s_n = nd - (n - nd) = 2nd - n

nd admet les valeurs 0,1,2,··· ,n ainsi

s_n ? {-n,-(n-2),···,n-2,n}

Proposition 3. La probabilité d'un chemin (S0,S1,··· ,S_n) pour une marche aléatoire à n pas est égale à _2n1 .

Remarque 3. Tous les chemins sont équiprobables.

Démonstration. Considérons un chemin (S0 = s0,S1 = s1,··· ,S_n = s_n).On a s0 = 0 et si - si_1 ? {-1,+1} pour i = 1,2,··· ,n. On a

P{S0 = s0,S1 = s1,··· ,S_n = s_n}

Alors

P{S0 = s0,S1 = s1,···,S_n = s_n} = P{M1 = s1 - s0,M2 = s2 - s1,···,M_n = s_n -sn_1}

= _Yn

i=1

1

P{Mi = si - si_1}

=

2n

PuisqueP{Mi =si-si_1}= ¹₂,?i ? {1,··· ,n}

n+s_n

2

Proposition 4. Considérons un point A = (n,sn). Le nombre de chemins possibles entre l'origine et le point A est

Nn,s_n = Cnd

n = C_n

Le nombre de chemins di~érents avec n pas est égale à 2ⁿ.

Proposition 5. Notons la probabilité que la particule arrive au point S_n = s_n à l'instant n, par pn,sn.Ainsi :

1 1 n+sn

P{S_n = s_n} = pn,sn = 2n Nn, = 2n Cn ²

Démonstration. Si S_n = s_n,et s'il y a eu nd pas vers la droite et n_g pas vers la gauche, on a nd -n_g = s_n et nd +n_g = n. On trouve nd = n+sn

2 et n_g = n_sn

2 . Le nombre de chemins

distincts est le nombre de manières de placer les nd pas vers la droite parmi les n pas,

n+s_n

soit Cnd

n = C_n . Tous les chemins ont la même probabilité 1

2 2n , d'où le résultat.

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

13

Principe de réfléxion

Théorème 1.2. Soient n,b > 0 et s_n > 0, alors le nombre de chemins joignant (0,b) à (n,s_n) et touchant l'axe des abscisses est exactement le nombre de chemins joignant (0,-b) à (n,s_n)

Théorème 1.3. Soit n,s_n ? Z +, le nombre de chemins (s0,s1,··· ,s_n) de l'origine s0 = 0 au point (n,s_n) tel que

s1 > 0,s2 > 0,···,s_n-1 > 0,s_n > 0

est donné par

sn Nn-1,sn-1 - Nn-1,sn+1 = n

Nn,sn

Retour à l'origine

Remarque 4. Pour un retour à l'origine à un instant n, l'instant n considéré doit être nécessairement pair. Nous allons donc considérer des instants de la forme 2n. On note u2n la probabilité qu'il y ait un retour à l'origine à un instant 2n.

Lemme 1. la probabilité qu'il y ait un retour à l'origine à un instant 2n est égale à

= P{_S2n = 0ll 1

u C

_2n T _I = P2n n

_,0 = 2n 2n

u2n = 1 pour n = 0.

Démonstration. On applique la proposition 5 au points (0,0) et (2n,0)

1 1 2n+0

2

P{î2n = 0} = p2n,0 = 22n N2n,0 = 22n C2n

d'où le résultat.

Approximation de u2n par la formule de Stirling

Approximation de la probabilité d'un retour à l'origine à l'instant 2n par la formule de Stirling pour un n grand

1

u2n '

Démonstration. Formule de Stirling n! ' v2ðn (ne ) n

On a donc (2n)! ' v4ðn (2é) n et (n!)² ' 2ðn^l(é)²ⁿ

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

alors

(2n)!

u2n = (n!)2 2-2n

(2n 1)2n

v4ðn e-2n

' 27rn (7,,,) 2n 2

_eJl

1

'

Premier retour à l'origine

Définissons l'instant du Premier retour à l'origine par

T0 = inf{n = 0, n = 0} avec convention inf(Ø) = +8

La probabilité que le premier retour à l'origine soit à l'instant 2n. Noté par f2n tel que

f2n = P{T0 = 2n}

Relation entre u2n ^et f2n

Pour n = 1

u2n =

Xn k=1

u2n-2kf2k

Théorème du retour à l'origine

Théorème 1.4. La probabilité qu'il y ait un retour à l'origine jusqu'à l'instant 2n compris est égale à la probabilité qu'il y ait un retour à l'instant 2n :

P{ 1 # 0, 2 # 0,··· , 2n # 0} = P{ 2n = 0} = u2n (1.1)

Les _i étant tous positifs ou tous négatifs (avec la même probabilité), on a :

1 1

P{ 1 > 0, 2 > 0,··· , 2n > 0} = ₂P{ 2n = 0} = ₂u2n (1.2)

Démonstration. Nous démontrons l'équation (1.2) On ana

P{ 1 > 0, 2 > 0,···, 2n > 0} =

14

00

P{ 1 > 0, 2 > 0,···, 2n = 2s_n} sn=1

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

(Les termes de la somme avec s_n > n sont nuls). d'après le théorème(1.2)

l 1

P{ 1 > 0, 2 > 0,··· , 2n = 2s_n} = 2n N2n-1,2s_n-1 - N2n-1,2s_n+1

Alors

P{ 1 > 0, 2 > 0,···, 2n > 0} =

00 sn=1

2n 1 {N2n-1,2sn-1 - N2n-1,2sn+1}

Elle reste

1 2n

1 n 1 N2n-1,1 = 2nC2n-1 = 2u2n

D'après le théorème du retour à l'origine, la particule n'est pas retournée à l'ori-gine jusqu'à l'instant 2n - 2 compris avec la probabilité u2n-2. Au temps 2n, soit elle revient à l'origine (c'est donc pour la première fois) avec la probabilité f2n, soit elle n'y revient pas avec la probabilité u2n. Autrement dit, Pour n = 1,2,··· ,N

f2n = u2n-2 - u2n

On particule

¹n-1

f2n = 22n-1C2n-2 -u2n

Alors

1 (2n - 2)!

(( n - 1)!)2 - u2n

f2n =

22n-1

Donc

1 (2n)! 4n²

f2n =

22n ((n)!)² (2n - 1)2n - u2n

15

D'où

1

f2n = (2n - 1)^u2n

Dernier retour à l'origine

Rappel La fonction de répartition de la loi arc sinus standard est donnée par :

2 arcsin(vx) F (x) = ð

Pour 0 < x < 1, et dont la densité de probabilité est donnée par :

f(x) =

1

\I ð x(x -1)

sur ]0,1[ . La loi arc sinus est un cas particulier de la loi bêta avec les paramètres á = â = ¹₂. Ainsi si X est de loi arc sinus standard alors X ti Beta(¹₂, ¹₂)

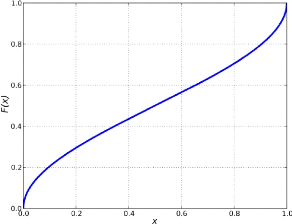
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

FIGURE 1.1 - Représentation graphique de F(x)

Théorème 1.5. La probabilité que la dernière visite à 0 avant le temps 2n se produise au temps 2k est donné par

á2k,2n = P{î2k = 0,î2k+1 # 0,··· ,î2n # 0} = u2ku2n-2k Théorème 1.6. Si î0 = 0, pour n = 0

P{î1 ×î2 ×···×în # 0,în = sn} = |sn| n

P{în = sn} (1.3)

Par conséquent

P{î1 × î2 ×···× î2n # 0} =

n

E{|î_n|}

1

X snEZ

X P{î1 ×î2 ×···×în # 0,în = sn} = snEZ

|sn| n

P{în = sn}

16

Démonstration. Prenons d'abord s_n > 0. Le nombre de chemins dans l'événement considéré par le théorème (1.2) snn Nn,s_n, et chaque chemin a n+sn 2 pas vers la droite et n-sn

2 vers

la gauche. Donc

P{tt tt tt S1 × S2 × ··· × în # 0,Sn = sn} = sn

( Nn sn G)2 n+sn) (2) 1 12 (n )--sn

. Même our s_n < 0 (on applique le principe de réflexion) d'où le résultat. On a

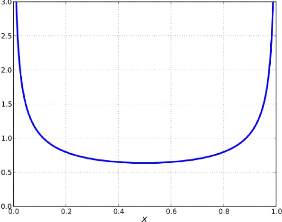
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

FIGURE 1.2 - Représentation graphique de f(x)

Donc

1 P{?sn?Z (S1 × S2 × ··· × Sn # 0) n Sn = sn} = n

E{|Sn|}

P{S1 ×S2 × ··· ×S_n # 0n(?s_nEgn = s_n)} =

n

1

E{|S_n|}

s_n=2m

= E P{S1 ×S2 × ··· × S2m # 0,S2m = s_n} s_n=-2m

=

sn=2m E sn=-2m

|sn| 2m

P{S2m = sn}

17

1

P{S1 × S2 × ··· × Sn # 0 n Ù} = n		E{|Sn|}	1 P{S1 ×S2 ×···×Sn # 0} = n
E{|Sn|}

Démonstration. (théorème 1.3) tt

á2k,2n = P{S2k = 0,S2k+1 # 0,··· ,S2n # 0}

= P{S2k = 0}P{S2k = 0,S2k+1 # 0,···/S2_n # 0}

= P{S2k = 0}P{S2k = 0,S2k+1 # 0,··· ,S2n-2k # 0}

On pose m = n- k montrons que P{S2k = 0,S2k+1 # 0,··· ,S2m # 0} = P{S2m = 0}

P{S2k = 0,S2k+1 # 0,··· ,S2m # 0} = P{S1 ×S2 × ··· × S2m # 0}

T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

P{î1 X î2 X ··· X î2m # 0} = 2

Xm k=1

2k 2m

P{î2m = 2k}

_Xm k=1

= 2

2k 1

_Cm+k

2m

2m2²m

Montrons que

2k Cm+k

2m = Cm+k-1

2m-1 - Cm+k

2m-1

2m

On a

(2m - 1)! (2m - 1)!

_Cm+k-1

2m-1 - Cm+k

(m+k -1)!((2m-1-(m+k -1))! (m+k)!((2m-1-(m+k))!

2m-1 =

"= (2m -1)!

# 1 1 (m+k -1)!(m-k)! ^-(m+k)!(m-k -1)!

= (2m -1)! Lm+k)!(m-k)!]

(m+k)-(m-k

(2m -1)! =2k
(m+k)!(m - k)!

2k 2m

(2m)!

=

(m+k)!(m - k)!

= 2k Cm+k

2m 2m

Donc

P{î1 X î2 X ··· X î2m # 0} = 2

Xm k=1

2 1 rCm+k-1 - Cm+k 1 L 2m-1 2m-1]

1 m

= 2 X 22m C2m-1

1 =C^m = P{î2m = 0} 22m 2m

Alors

18

á2k,2n = P{î2k = 0}P{î2_m = 0} = P{î2k = 0}P{î2n-2k} = u2ku2n-2k

La représentation graphique de la distribution discrète de l'arc-sinus à n = 50

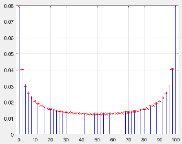
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

Remarque 5. La distribution á2k,2n est symétrique par rapport à n, on a donc :

á2k,2n = á2n-2k,2n

On donne maintenant l'approximation de la probabilité á2k,2n à l'aide de la formule de Stirling.

Rappelons que :

1 1

P{î2k = 0} ' v et P{î2n-2k = 0} ' _q

ðkð(n - k)

Alors

1 1

Ck 2kCn-k

2n-2k ' _q

22n ð

á2k,2n =

(n - k)

' 1

n

1

q k

ð _n(1 - ^k_n)

Si on pose

1

f(x) =

qð x(1 - x)

On voit que

á2k,2n '

1 f(tk) avec tk = k

n n

si n -? 8 alors tk devient une variable continue et t ? [0,1] On intégrant f

X F(t) = n<t k

X á2k,2n ' n<t k

1 n

k !f n

19

ft f(x)dx = 2 arcsinvt

F(t) donnera la probabilité que le dernier retour à l'origine arrive avant le temps relatif

k n

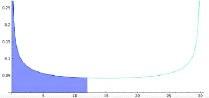
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX

20

Interprétation de f(t) et F(t) à l'aide d'un exemple Prenons une marche aléatoire de 30 pas, c'est-à-dire n = 30. Choisissons l'intervalle I = [0,12] et regardons la probabilité que le dernier retour à l'origine soit dans l'intervalle considéré. L'aire bleu foncée visualisé sur la figure ci-dessus sous la courbe de f(t) et dans l'intervalle I donne la probabilité approximée que le dernier retour à l'origine soit avant le temps k = 12. La valeur approximative de l'aire est donné par:

2 F(t) ' ð

/ arcsin t

où t = k n

comme n = 30 et k = 12 on a t = 12

30 = 0.4. Ainsi

2 F (0.4) ' ð

J arcsin 0.4 0.4359

La probabilité que le dernier retour à l'origine soit avant le temps 12, dans une marche

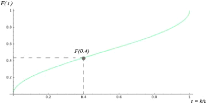
aléatoire de 30 pas, est d'environ 0,4359.