Pour calculer des intervalles de confiance
prévisionnels et aussi pour effectuer les tests de Student sur les
paramètres, il convient de vérifier la normalité des
erreurs. Le test de Jarque et Bera (1984), fondé sur la notion de
Skewness (asymétrie, caractérise le fait que la loi normale est
une loi symétrique) et de Kurtosis (aplatissement, nous indique le
degré d'aplatissement des queues de distribution), permet de
vérifier la normalité d'une distribution statistique.Tapez une
équation ici.
Le test de normalité :
- Les test du Skewness et du
Kurtosis
Soit k = 
? (
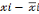)k le moment
centré d'ordre k.
3
Le coefficient de Skewness (11/2)
est : 11/2 = -----------
23/2
4
Le coefficient de Kurtosis (2)
est : 2 = --------
22
Si la distribution est normale et le nombre d'observations
grand ( plus grand que 30) alors :
3
11/2 = ----------- ~
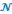(0 ;
)
23/2
4
2 = ------------- ~
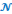(3 ;
)
22
On construit alors les statistiques :
11/2 - 0
2 - 3
1 = ----------------- et
2 = ----------------- que l'on compare à
1,96 (valeur de
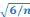
la loi normale au seuil = 5%). Si les hypothèses (H0)
1 = 0 (symétrie) et 2 = 0 (aplatissement normal)
sont vérifiés, alors 1 
1,96 et 2 =
1,96 ; dans le cas contraire l'hypothèse de normalité est
rejetée.
- Le test de Jarque et Bera :
Il s'agit d'un test qui synthétise les résultats
précédents ; si 11/2 et 2
obéissent à des
lois normales alors la quantité s = 
11/2 +
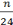(2 -
3)2 suit un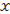 
2 à deux degrés de liberté. Donc si s
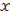2(2), nous
rejetons l'hypothèse (H0) de normalité des résidus au
seuil .
Observons les résultats obtenus dans RATS :
Skewness -0.126742 Signif Level (Sk=0)
0.441764
Kurtosis (excess) 0.616728 Signif Level (Ku=0)
0.063624
Jarque-Bera 4.149665 Signif Level (JB=0)
0.125577
La Skewness et la Kurtosis suivent bien une loi normale car
1 et 2 sont inférieurs à 1,96.
La valeur tabulée dans la table de CHI2
à deux degrés de liberté et au seuil = 5% est de 5,991
> 4.149665, nous acceptons donc l'hypothèse (H0) de normalité
des résidus.
Le test d'auto-corrélation :
Il s'agit des tests de Durbin-Watson, du h de Durbin et de Ljung-Box qui ont
été expliqués auparavant.
Nous allons étudier directement les résultats.
Durbin-Watson Statistic 1.665146
Nous observons un Durbin-Watson éloigné de 2, nous
pouvons supposer la présence d'auto-corrélation dans le
modèle.
Q(4-0) = 10.0546. Significance Level 0.03951826
La valeur tabulée dans la table de CHI2
pour 4 degrés de liberté et au seuil = 5% est de 9,488. Nous
avons donc un Q calculé > Q tabulé nous rejetons
l'hypothèse (H0) absence d'auto-corrélation, il y a de
l'auto-corrélation d'un ordre supérieur à 1.
Q(28-0)= 44.4877. Significance Level 0.02484545
La valeur tabulée dans la table de CHI2
pour 28 degrés de liberté et au seuil = 5% est de 41,337. Nous
avons donc un Q calculé > Q tabulé nous rejetons
l'hypothèse (H0) absence d'auto-corrélation, il y a de
l'auto-corrélation d'un ordre supérieur à 1.
Nous avons demandé au logiciel RATS de calculer les Q de
Ljung-Box avec un découpage des degrés de liberté allant
de quatre par quatre. Sur les sept sous périodes observées seules
ces deux là présentent de l'auto-corrélation.
Il existe plusieurs méthodes pour retirer
l'auto-corrélation (Cochrane-Orcutt et Hidreth Lu). Nous n'utiliserons
que la méthode de Cochrane-Orcutt. Avant de l'utiliser, nous allons
faire sa description théorique.
On part d'un modèle initial :
Yt = a + b.Xt + t
On transforme le modèle initial :
Yt - 
.Yt-1 = a.(1 - 
)
+ b.(Xt - 
.Xt-1) + ut
avec ut = t - t-1
On reprend cette équation. On sait que ñ
appartient à l'intervalle [0 ; 1]. On va définir un pas pour
ñ (0,1 ; 0,2 ; ... ; 1) et on estime le modèle
pour chaque pas. On retiendra le modèle pour lequel la valeur de
ñ minimise le « s » c'est-à-dire qui minimise
la somme des carrés des résidus.
Observons le résultat obtenu,
6. RHO 0.280994577 0.066862456
4.20258 0.00003850
Donc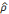 
= 0.280994577 est la valeur qui permet de retirer
l'autocorrélation.
Le test
d'hétéroscédasticité :
Le test de White (1980)
C'est le test le plus général car nous y
introduisons toutes les formes d'hétéroscédasticité
possibles. Il est fondé sur une relation significative entre le
carré du résidu et une ou plusieurs variables explicatives en
niveau et au carré au sein d'une même équation de
régression :
et2 = a1 x1t +
b1 x1t2 + a2 x2t +
b2 x2t2 +...+ ak xkt +
bk xkt2 + a0 + 
t
Soit n le nombre d'observations disponibles pour
estimer les paramètres du modèle et R2 le coefficient
de détermination. Si l'un de ces coefficients de régression est
significativement différent de 0, alors nous acceptons
l'hypothèse d'hétéroscédasticité. Nous
pouvons procéder à ce test par un test de Fisher classique de
nullité de coefficients ou recourir à la statistique LM qui est
distribuée comme un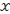 
2 à p = 2k degrés de liberté.
(H0) a1 = b1 = a2 =
b2 =....= ak = bk = 0
homoscédasticité
(Ha) au moins une contrainte non vérifiée
hétéroscédasticité
Règle de décision :
Pour le test de Fisher
Si le F calculé > F tabulé, on rejette (H0)
pour dire qu'il y a hétéroscédasticité
Pour le test LM
Si LM calculé > LM tabulé, on rejette (H0)
pour dire qu'il y a hétéroscédasticité
Observons les résultats obtenus,
Regression F(14,208) 1.4708
Le F tabulé dans la table de Fisher pour 1 =
12 et 2 = 8 et au seuil = 5% est de 1,75. Nous avons donc un F
calculé < au F tabulé, nous acceptons l'hypothèse nulle
d'homoscédasticité
Chi-Squared(14)= 20.087209 with Significance Level
0.12741580
Le LM tabulé dans la table de CHI2 pour
quatorze degrés de liberté et au seuil = 5% est de 23,685. Nous
avons donc un LM calculé < au LM tabulé, nous acceptons donc
l'hypothèse nulle d'homoscédasticité.
Nous pouvons conclure que notre modèle possède
des erreurs homoscédastiques.
