Contribution à la caractérisation mécanique des critères de qualités du départ de la course vitesse sur 100 m

Effet d'une procedure de solidification par recurrence

sur la cinematique et dynamique articulaires

1-Proposition d'une nouvelle procedure de solidification

Afin de minimiser les artéfacts dus aux mouvements de la peau (ADMP) tout en conservant les contraintes de liaison propres à chaque articulation et sans modifier l'orientation mesurée des segments (§-VII.5), il est possible de procéder comme suit.

Etape 1 : Determination des positions et orientations relatives des segments

Suite à l'approximation des centres articulaires (§-VII.2.2), l'attribution d'un repère

dynamique/technique ~ iDyn/Tech à chaque segment et la définition de l'opérateur homogène

i Dyn / Anat

T (§-VII.2.1), la matrice ⁱ⁺¹

T i Dyn / Anat décrivant la position et l'orientation relative d'un

0

segment Si+1 par rapport à un segment Si est définie par :

Ti ⁱD⁺yn¹ / Anat = Ti0 Dyn/ Anat · T ⁱ⁺¹Dyn/ Anat Éq.VIII. 16 0

tel que ( ) - 1

T i Dyn / Anat T 0 Dyn / Anat

0 i

? Etape 2 : Définition des longueurs segmentaires

La position de l'origine d'un repère Ri Dyn/ Anat d'un segment Si est coïncidente avec le

centre articulaire de ce segment (§-VII.2.2). La distance entre un repère proximal

ai+1 Dyn/ Anat et un repère distal a.i Dyn/ Anat correspond donc à la longueur			~~ Li	de Si. Cette
relation se formule de la manière suivante :

~ ~ ~

= ( O - O ) i + ( O - O ) j + ( O - O ) k

2 2 2

i+1 i i+1 i i+1 i

Éq.VIII. 2

~~

L i

~ - -

dont O_i et ( i, j, k) correspondent respectivement à l'origine et à la base orthonormée

directe de ai Dyn/ Anat . O_i+1 est l'origine de a_i+1 Dyn/ _Anat .

§ Etape 3 : Expression de la longueur dans le repere segmentaire correspondant L'axe Y est l'axe proximodistal de a_{i Dyn}/ _Anat passant par O_i et _Oi+1 (§-VII.2). Ce

~~

dernier point permet de définir directement les composantes de Li dans ~i Dyn/ Anat .

~~ ~ ~ ~

L = 0 i + l j + 0 k i Éq.VIII. 3

tel que l est la longueur du segment définit suite aux relevés des mesures anthropométriques.

§ Etape 4 : Solidifier les segments de la cha'ine cinématique

La matrice de transformation homogène i+1

T i Dyn / Anat dont les colonnes sont les

composantes des vecteurs de ai+1 Dyn/ Anat dans ai Dyn/ Anat se définit comme suit :

T

i +1

i Dyn/ Anat

Éq.VIII. 4

( O _i O i+1) iR ( O _i O i+1)( O _i O i+1)k0 0 0 1i+1

Tenant compte des trois premières étapes, il est possible de définir les termes du vecteur translation de cette matrice.

En effet, étant à l'origine de la construction de l'axe proximodistal Y de chaque segment, les coordonnées des centres articulaires doivent être nuls suivants les axes segmentaires antéropostérieur X et médiolatéral Z. De plus, la distance entre les deux centres fonctionnels doit être constante en fonction du temps. Ainsi, à tout instant, la matrice de

passage homogène de ai Dyn/ Anat à ai+1 Dyn/ Anat s'écrit :

0

T i +1

i Dyn/ Anat

Ri+1 l

i i

0

0 0 0 1

La mise en place d'une contrainte de position au niveau du vecteur translation de

l'opérateur homogène i+1

T i Dyn / Anat permet de fixer la position d'un repère ai+1 Dyn/ Anat par

rapport à son homologue ai Dyn/ Anat .

Li

De ce fait la distance

entre deux centres articulaires proximal et distal d'un

même segment reste constante tout en conservant l'orientation originelle du repère segmentaire. Un raisonnement par récurrence permet alors de solidifier les autres segments de la chaîne cinématique.

Dans le cas de cette étude, vue l'orientation des repères segmentaires déjà définie (§- VII.2), le raisonnement par récurrence suit l'arborescence suivante (figure 85) :

Bras

Segments droits ?

T Pied T Jambe T Cuisse

Jambe Cuisse Pelvis

? T Bras T Av.bras

Tête ^??

Tronc T Pelvis

Abdomen ? T Abdomen T Thorax

Thorax Tête

^?Bras

Segments gauches ?

T Pied T Jambe T Cuisse

Jambe Cuisse Pelvis

? T Bras T Av.bras

Tête ??

Figure 85 Arborescence de la chaîne cinématique

La figure 86 illustre l'exemple de la variation instantanée de l'intensité du vecteur

LCuisse

dans aCuisse Dyn/ Anat avant et après l'application des contraintes sur les positions des

centres articulaires.

Avant Après

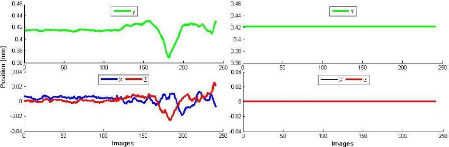
Figure 86 Position du repère pelvis droit par rapport au repère cuisse droite avant et après
l'application des contraintes de position suivant les trois dimensions de l'espace

Etape 5 : Definition des positions et orientations absolues des segrnents rigidifies Suite à la redéfinition de toutes les matrices ⁱ⁺¹

T i Dyn

/ Anat , une dernière transformation est

effectuée afin d'exprimer la position et l'orientation des repères segmentaires a_i+1 Dyn/ Anat

dans g0. L'équation de cette transformation s'écrit :

T i +1 Dyn/ Anat T i Dyn/ Anat _Ti+1

·i Dyn/ Anat Éq.VIII. 5 0 0

1.1-Effet de la PSR sur la configuration du systerne poly-articule

Suite à l'application de la procédure de solidification par récurrence (PSR) et l'expression de la chaîne cinématique des segments rigides poly-articulés dans R0, il importe de déterminer son effet sur la définition de la position des repères segmentaires.

Rappelons que l'orientation mesurée (originale, brute) des repères segmentaires est conservée suite à l'application de la PSR.

Dans les figures qui suivent (figures 87, 88 et 89) est exposée la différence entre les positions des centres articulaires⁴⁸ mesurées et recalculées suite à l'application de la PSR.

⁴⁸ La position d'un centre articulaire d'une articulation coïncide, par définition, avec l'origine du repère segmentaire amont. Exemple : le centre articulaire du genou coïncide avec l'origine du repère cuisse (fémur).

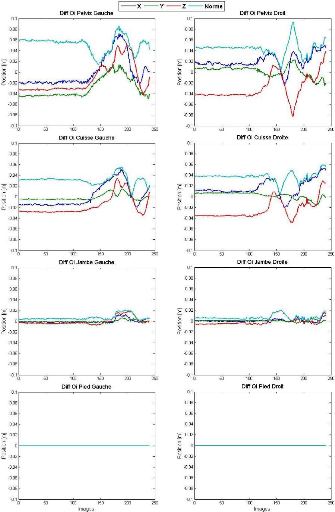
Figure 87 Différences entre les positions mesurées (brutes) et recalculées
des centres articulaires Oi des membres inférieurs

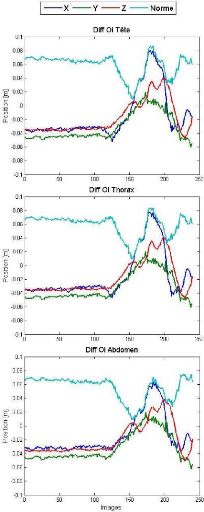
Figure 88 Différences entre les positions mesurées (brutes) et recalculées
des centres articulaires Oi de la tête, du thorax et de l'abdomen

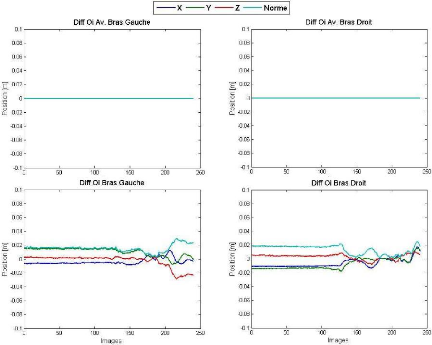
Figure 89 Différences entre les positions mesurées (brutes) et recalculées
des centres articulaires Oi des membres supérieurs

L'écart moyen le plus important entre les positions mesurées (brutes) et recalculées des centres articulaires (Oi) est de 5 #177;1 cm atteint au niveau de Oi tête (figure 88). Suite à l'adoption des recommandations de l'ISB [Wu 02, Wu 05] (§-VII.2), les origines des repères segmentaires des bras et des pieds représentent les points de départ du raisonnement par récurrence (figure 85). Les écarts entre les positions de Oi mesurées et recalculées de ces segments sont donc quasi nuls (figures 87 et 89).

Il importe de rappeler ici que l'objectif attendu, suite à l'adoption d'une procédure de minimisation des artéfacts, est de pouvoir appliquer les principes de la mécanique des solides rigides [Capp 05]. La méthode adoptée doit donc fixer les longueurs segmentaires tout au long du geste enregistré.

Contrairement aux procédures d'optimisation par moindres carrés, la PSR :

§ n'entraîne pas de dislocations articulaires (§-VII.5), puisqu'elle met des contraintes de

positions au niveau des centre articulaires (§-VIII.1. Étape 2 et 3) ;

§ ne modifie pas l'orientation des segments et de ce fait n'entraîne pas l'accumulation

d'incertitude de mesure (§-VII.5), puisqu'elle ne modifie que la position du segment en conservant ses orientations (§-VIII.1. Étape 4 et 5) ;

§ nécessite un temps de calcul vingt cinq fois plus court (6 s contre environ 150 s).

Dans ce qui suit, l'estimation des grandeurs cinématiques segmentaires et dynamiques articulaires est réalisée suite à l'adoption de la PSR et la procédure de solidification globale (PSG) proposée par Lu et O'Connor (1999). Les grandeurs calculées en appliquant ces deux procédures (PSR et PSG) sont confrontées afin d'estimer les éventuelles différences.