|
UNIVERSITE DE TUNIS EL MANAR FACULTE DES
SCIENCES DE TUNIS
|
|
|
|
ECOLE DOCTORALE EN INFORMATIQUE
F
MEMOIRE DE MASTERE
présenté en vue de l'obtention
du
Diplome de Mastere en In formatique
par
Tarek HAMROUNI
Maitrise en Informatique, FS de Tunis)
Extraction des bases
génériques
informatives de règles sans calcul
de fermetures
soutenu le 14 juillet 2005, devant le jury d'examen
MM. Habib OUNELLI Président
Mohamed Mohsen GAMMOUDI Membre
Yahya SLIMANI Directeur du memoire
Sadok BEN YAHIA Invite
Dedicaces
Ce travail est dedie a mes Maitres, rues
parents et ma famille.
Qu'ils trouvent ici le Mmoignage de ma gratitude et de
mon
respect.
REMERCIEMENTS
C'est avec un grand plaisir, que j'exprime ici ma
reconnaissance a tous ceux qui m'ont apporté leur aide scientifique,
matérielle ou morale pour mener a terme ce travail.
A Mr. Habib Ounelli, Maitre de Conférences a la
Faculté des Sciences de Tunis, pour avoir accepté de
présider le jury de ce Mastère. Je le remercie pour l'attention
avec laquelle il a lu et évalué ce mémoire.
A Mr. Mohamed Mohsen Gammoudi, Maitre Assistant a la
Faculté des Sciences de Tunis, pour avoir accepté de participer
au jury de ce Mastère. Je le remercie pour l'attention avec laquelle il
a lu et évalué ce mémoire.
A Mr. Yahya Slimani, Maitre de Conférences a la
Faculté des Sciences de Tunis, pour ses orientations, ses conseils et
ses suggestions. J'ai spécialement apprécié son esprit
critique et sa rigueur scientifique. Qu'il trouve ici l'expression de mon
respect.
A Mr. Sadok Ben Yahia, Maitre Assistant a la Faculté
des Sciences de Tunis, qui m'a aidé dans ce travail et en a rendu
possible la réalisation. J'ai particulièrement
apprécié ses qualités humaines indéniables, sa
disponibilité et ses conseils de bon aloi. Qu'il trouve ici l'expression
de ma gratitude.
Je souhaite aussi exprimer toute ma reconnaissance envers Mr.
Yves Bastide, Professeur adjoint a l'Ensar de Rennes, qui s'est montré
toujours disponible a répondre a mes questions et pour avoir mis a ma
disposition les codes sources des algorithmes CLOSE, A-CLOSE et TITANIC
utilisés dans le cadre de ce travail.
Je tiens également a remercier Mlle Yosr Slama,
Assistante a la Faculté des Sciences de Tunis, pour son aide a
l'élaboration de l'étude théorique de la complexité
de l'algorithme proposé.
Je remercie les membres de l'URPAH de la Faculte des Sciences de
Tunis de m'avoir accueilli au sein de leur unite et fait beneficier de leurs
experiences.
Mes remerciements vont aussi a tous ceux qui, non cites ici,
m'ont soutenu tout le long de ce travail.
Résumé: Durant ces
dernières ann'ees, les quantit'es de donn'ees collect'ees, dans divers
domaines d'application de l'informatique, deviennent de plus en plus
importantes. Ces quantit'es ont suscit'e le besoin d'analyse et
d'interpr'etation afin d'en extraire des connaissances utiles. Ce m'emoire
s'int'eresse a` la technique d'extraction de règles associatives, une
des techniques les plus utilis'ees dans le domaine de la fouille de donn'ees.
La première approche permettant la g'en'eration de règles
associatives s'est bas'ee sur l'extraction des itemsets fr'equents. Cependant,
cette approche souffre de deux problèmes majeurs, a` savoir le coüt
de l'extraction des itemsets fr'equents, qui sont n'ecessaires a` la
g'en'eration de règles associatives, et la g'en'eration d'un nombre
important de règles associatives, dont un bon pourcentage est redondant.
Pour rem'edier a` ces problèmes, une nouvelle approche bas'ee sur la
d'ecouverte des itemsets ferm'es fr'equents en utilisant les treillis de
Galois, issus de l'analyse formelle de concepts, a 'et'e
propos'ee. Toutefois, les algorithmes relatifs a` cette nouvelle approche se
sont focalis'es sur la r'esolution du premier problème, sans se soucier
de la construction de la relation d'ordre partiel li'ee a` un treillis de
Galois. Cette relation est une condition sine qua non pour
l'extraction, sans perte d'information, d'un sous-ensemble de règles
associatives, appel'e base g'en'erique. Dans ce cadre, nous avons propos'e un
nouvel algorithme appel'e PRINCE pour la g'en'eration de bases g'en'eriques de
règles associatives. Cet algorithme effectue une exploration par niveau
de l'espace de recherche. Sa principale originalit'e est qu'il est le seul a`
construire la relation d'ordre partiel dans l'objectif d'extraire les bases
g'en'eriques de règles. Pour r'eduire le coüt de cette
construction, la relation d'ordre partiel est maintenue entre l'ensemble des
g'en'erateurs minimaux des itemsets ferm'es fr'equents et non plus entre les
itemsets ferm'es fr'equents. Une structure, appel'ee treillis des
générateurs minimaux, est alors construite a` partir de
laquelle la d'erivation des bases g'en'eriques devient imm'ediate. Les
exp'erimentations que nous avons r'ealis'ees sur diff'erents contextes
d'extraction ont montr'e l'efficacit'e de l'algorithme propos'e,
comparativement a` des algorithmes de r'ef'erence tels que CLOSE, A-CLOSE et
TITANIC.
Mots-clés: Fouille de donn'ees, Analyse
formelle de concepts, Itemsets (ferm'es) fr'equents, Treillis de
Galois, Treillis des générateurs
minimaux, Règles associatives, Base
générique de règles.
Abstract: In the last few years, the amount
of collected data, in various computer science applications, becomes
increasingly significant. These large volumes of data pointed out the need to
analyze them in order to extract useful hidden knowledge. This Master thesis
focusses on the association rule extraction, one of the most popular knowledge
extraction technique. The first approach to extract association rules, uses the
notion of frequent itemsets. However, this approach suffers from two major
problems, namely the cost of extracting frequent itemsets and the high number
of extracted association rules, among which many are redundant. Thus, a new
approach based on Galois lattice uses the notion of frequent closed itemsets
instead the frequent ones. However, algorithms related to this new approach
have only resolved the first problem and have avoid the problem of construction
of the order relation associated to a Galois lattice. This partial order
relation is a sine qua non condition to obtain a subset of all
association rules, without information loss, called generic basis. For this
purpose, we proposed a new algorithm called PRINCE that performs a level-wise
browsing of the search space. Its main originality is that it is the only one
which constructs the partial order in order to extract generic bases. In order
to reduce the cost of this construction, the partial order is maintained
between frequent minimal generators and not between frequent closed itemsets. A
structure called minimal generator lattice is then built, from
which the derivation of the generic association rules becomes straightforward.
Several experimentations of our algorithm have showed the efficiency of the
proposed algorithm, comparatively to well-known algorithms like CLOSE, A-CLOSE
and TITANIC.
Key-words: Data mining, Formal concept
analysis, Galois lattice, Frequent (closed) itemsets, Minimal
generator lattice, Association rules, Generic
rule basis.
Table des matières
|
Introduction generale
1 Fondements mathematiques pour l'extraction de regles
d'association
|
1
5
|
|
1.1
|
Introduction . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
5
|
|
1.2
|
Dérivation des regles d'association . . . . . . . . . .
. . . . . . . . . . . . .
|
7
|
|
|
1.2.1 Base de transactions . . . . . . . . . . . . . . . . . .
. . . . . . . .
|
7
|
|
|
1.2.2 Regles d'association . . . . . . . . . . . . . . . . . .
. . . . . . . . .
|
7
|
|
1.3
|
Analyse formelle de concepts . . . . . . . . . . . . . . . . .
. . . . . . . . .
|
9
|
|
|
1.3.1 Introduction . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . .
|
9
|
|
|
1.3.2 Notion d'ordre partiel . . . . . . . . . . . . . . . . .
. . . . . . . .
|
10
|
|
|
1.3.3 Connexion de Galois . . . . . . . . . . . . . . . . . . .
. . . . . . .
|
12
|
|
|
1.3.4 Itemsets fermés et leurs générateurs
minimaux . . . . . . . . . . . .
|
14
|
|
1.4
|
Dérivation des bases génériques de regles
d'association . . . . . . . . . . .
|
16
|
|
1.5
|
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
19
|
|
2
|
Algorithmes d'extraction des itemsets fermes frequents : Etat de
l'art
|
21
|
|
2.1
|
Introduction . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
21
|
|
2.2
|
Algorithmes d'extraction des itemsets fermés
fréquents . . . . . . . . . . .
|
22
|
|
|
2.2.1 Les algorithmes de type "Générer-et-tester"
. . . . . . . . . . . . .
|
23
|
|
|
2.2.2 Les algorithmes de type
"Diviser-et-générer" . . . . . . . . . . . . .
|
29
|
|
|
2.2.3 Les algorithmes hybrides . . . . . . . . . . . . . . . .
. . . . . . . .
|
32
|
|
2.3
|
Discussion . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
34
|
|
2.4
|
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
38
|
|
3
|
L'algorithme PRINCE
|
39
|
|
3.1
|
Introduction . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
39
|
|
3.2
|
L'algorithme PRINCE . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . .
|
40
|
|
|
3.2.1 Détermination des générateurs
minimaux . . . . . . . . . . . . . . .
|
41
|
|
|
3.2.2 Construction du treillis des générateurs
minimaux . . . . . . . . . .
|
46
|
|
|
3.2.3 Extraction des bases génériques
informatives de regles . . . . . . . .
|
50
|
|
3.3
|
Structure de données utilisée . . . . . . . . . .
. . . . . . . . . . . . . . . .
|
55
|
|
3.4
|
Preuves théoriques . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
|
57
|
|
3.5
|
Complexité . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . .
|
60
|
|
3.6
|
Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . .
|
64
|
4 Ètude experimentale 65
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 65
4.2 Environnement d'expérimentation . . . .
. . . . . . . . . . . . . . . . . . . 66
4.2.1 Environnement materiel et logiciel . . . . . . . . . . . .
. . . . . . . 66
4.2.2 Description des executables . . . . . . . . . . . . . . . .
. . . . . . 66
4.2.3 Bases de test . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 66
4.3 Optimisations et evaluations . . . . . . . . . . . . . . . .
. . . . . . . . . . 68
4.4 Effets de la variation de la mesure minconf . . .
. . . . . . . . . . . . . . . 74
4.5 Comparaisons des coits des
étapes de PRINCE . . . . . . . . . . . . . . . . 75
4.5.1 Bases benchmark . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 76
4.5.2 Bases "pire des cas" . . . . . . . . . . . . . . . . . . .
. . . . . . . 82
4.6 Performances de PRINCE vs. CLOSE, A-CLOSE et TITANIC .
. . . . . . . . 83
4.6.1 Bases benchmark . . . . . . . . . . . . . . . . . . . . . .
. . . . . . 83
4.6.2 Bases "pire des cas" . . . . . . . . . . . . . . . . . . .
. . . . . . . 90
4.7 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 93
Conclusion generale 93
Table des figures
1.1 Exemple de contexte formel . . . . . . . . . . . . . . . . .
. . . . . . . . . 9
1.2 Join - Meet . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . 11
1.3 Join-irréductible - Meet-irréductible . . . .
. . . . . . . . . . . . . . . . . . 12
3.1 Contexte d'extraction 1C . . . . . . . . . . . . .
. . . . . . . . . . . . . . . 56
3.2 Construction du treillis des generateurs minimaux et le
treillis d'Iceberg
associés au contexte d'extraction 1C pour
minsup2. . . . . . . . . . . . . . 56 3.3 Gauche : La base
générique de regles exactes BG. Droite : La
réduction
transitive des regles approximatives RI. . . . . . . . .
. . . . . . . . . . . . 56
3.4 Exemple d'un trie . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . 57
4.1 Exemple d'une base "pire des cas" avec n4 . . . . .
. . . . . . . . . . . . 68 4.2 La structure Itemset-Trie (Gauche) et la
structure IT-BDT (Droite)
associées au contexte d'extraction de la Figure 3.1 . . .
. . . . . . . . . . . 70 4.3 Effet de l'utilisation d'une représentation
compacte de la base sur les per-
formances de PRINCE . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 71
4.4 Effet de l'exécution de la procédure
GEN-ORDRE sur les performances de
PRINCE. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . 72
4.5 Effet de l'utilisation des 2-itemsets fréquents
non générateurs minimaux
sur les performances de PRINCE . . . . . . . . . . . . . . . .
. . . . . . . . 73 4.6 Effet de l'utilisation des listes prohibées sur
les performances de PRINCE . 74 4.7 Effet de la variation de minconf sur les
performances de PRINCE . . . . . . 75 4.8 Temps d'exécution des
étapes constituant PRINCE pour les bases denses . . 77 4.9 Temps
d'exécution des étapes constituant PRINCE pour les bases
éparses . 82 4.10 Temps d'exécution des étapes constituant
PRINCE pour les bases "pire des
cas" . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . 83
4.11 Les performances de PRINCE vs. CLOSE, A-CLOSE et
TITANIC pour les
bases denses . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . 88
4.12 Les performances de PRINCE vs. CLOSE, A-CLOSE et
TITANIC pour les
bases éparses . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . 91
4.13 Test de mise a l'échelle de PRINCE
vs. CLOSE, A-CLOSE et TITANIC pour
les bases "pire des cas" . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . 92
Liste des tableaux
|
2.1
|
Caractéristiques des algorithmes CLOSE, A-CLOSE, TITANIC,
CLOSET et
|
|
|
CHARM. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . .
|
37
|
|
3.1
|
Notations utilisées dans la procédure GEN-GMS . . .
. . . . . . . . . . . .
|
42
|
|
4.1
|
Description des exécutables des différents
algorithmes . . . . . . . . . . . .
|
66
|
|
4.2
|
Paramètres des bases synthétiques . . . . . . . . .
. . . . . . . . . . . . . .
|
67
|
|
4.3
|
Caractéristiques des bases benchmark . . . . . . . . . . .
. . . . . . . . . .
|
67
|
|
4.4
|
Tableau comparatif des étapes constituant PRINCE pour les
bases denses. .
|
78
|
|
4.5
|
Tableau comparatif des étapes constituant PRINCE pour les
bases éparses.
|
81
|
|
4.6
|
Tableau comparatif des étapes constituant PRINCE pour les
bases "pire des
|
|
|
cas". . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . .
|
84
|
|
4.7
|
Tableau comparatif des résultats expérimentaux de
PRINCE vs. A-CLOSE,
|
|
|
CLOSE et TITANIC pour les bases denses. . . . . . . . . . . . . .
. . . . . .
|
87
|
|
4.8
|
Tableau comparatif des résultats expérimentaux de
PRINCE vs. A-CLOSE,
|
|
|
CLOSE et TITANIC pour les bases éparses. . . . . . . . . .
. . . . . . . . .
|
94
|
|
4.9
|
Tableau comparatif des résultats expérimentaux de
PRINCE vs. A-CLOSE,
|
|
|
CLOSE et TITANIC pour les bases "pire des cas". . . . . . . . . .
. . . . . .
|
95
|
Liste des algorithmes
|
1
|
GEN-GMS
|
43
|
|
2
|
GEN-GMS-SUIVANT
|
44
|
|
3
|
GEN-ORDRE
|
50
|
|
4
|
GEN-BGRS
|
53
|
|
5
|
BASE-FIRE-CAS
|
69
|
Introduction générale
Il est chaque jour plus facile de collecter des donnees mais
notre capacite a en extraire des informations a forte valeur ajoutee reste
limitee [16]. Ainsi, l'attention des entreprises s'est progressivement
detournee des systemes operationnels, vitaux mais sans valeur ajoutee
concurrentielle reelle. Elle s'est alors portee sur des systemes decisionnels,
sans apport direct en matiere de productivite mais qui contribuent
veritablement a la differenciation strategique de l'entreprise [42]. Afin
d'exploiter ces masses importantes de donnees stockees dans les systemes
decisionnels, la fouille de donnees se propose de donner les outils et/ou
techniques necessaires pour l'extraction de cette connaissance. La fouille de
donnees (ou Data mining) est le domaine de recherche au sein duquel cooperent
statisticiens, specialistes en bases de donnees et en intelligence
artificielle, ou encore chercheurs en conception d'interfaces homme-machine
[16]. Les informations extraites, suite a l'application d'un processus de
fouille de donnees, peuvent prendre plusieurs formes, telles que les regles
d'association, les arbres de decisions, les reseaux de neurones, etc [24,
42].
Dans ce memoire, nous allons nous interesser, en particulier,
a la technique d'extraction de regles d'association. Cette technique a ete
introduite par Agrawal et al. en 1993 [1]. En 1994, Agrawal et al. ont propose
un des premiers algorithmes, appele APRIORI [2], pour l'extraction des regles
d'association a partir de bases de donnees des grandes surfaces commerciales.
Cet algorithme adoptait une strategie d'exploration par niveau de l'espace de
recherche, appelee "Generer-et-tester". Ainsi, le probleme d'extraction des
regles d'association est alors decompose en deux sous-problemes [2] :
1. Extraction des ensembles d'items (ou itemsets) interessants
(ou frequents) pour l'utilisateur, cad presentant une frequence d'apparition
superieure ou egale a un certain seuil minimal fixe par l'utilisateur.
Motivations
L'approche d'extraction des regles d'association -- basee sur
la decouverte des itemsets frequents -- souffre de deux problemes majeurs, a
savoir le coUt de l'extraction des itemsets frequents et surtout la generation
d'un tres grand nombre de regles, et ce meme pour de petites bases de
donnees.
Pour pallier ces inconvenients, une nouvelle approche basee
sur l'extraction des itemsets fermes frequents [48] est apparue. Cette approche
est issue des fondements mathematiques de l'analyse formelle de concepts
introduite par Wille en 1982 [66]. Cette nouvelle approche propose deux
alternatives seduisantes :
1. Une reduction du coUt de l'extraction des itemsets
frequents.
2. Une selection d'un sous-ensemble de toutes les regles
d'association, a partir duquel le reste des regles pourrait etre derive sans
perte d'information. Ce sous-ensemble de regles d'association est communement
appele base generi que.
Cependant, pour extraire ces bases generiques de regles, il faut
prealablement decouvrir trois composantes primordiales, a savoir [9] :
1. Les itemsets fermes frequents ;
2. La liste des generateurs minimaux associes a chaque itemset
ferme frequent ;
3. La relation d'ordre entre les itemsets fermes frequents.
Un survol critique des algorithmes, bases sur l'extraction des
itemsets fermes frequents, montre que les algorithmes existants dans la
litterature ont failli a leurs objectifs [9]. En effet, la quasi-totalite de
ces algorithmes se sont focalises sur l'extraction de la premiere composante,
cad les itemsets fermes frequents, en oubliant les deux dernieres. Seuls les
algorithmes adoptant la strategie "Generer-et-tester" font mieux en permettant
aussi l'extraction des generateurs minimaux, sans se soucier de la construction
de la relation d'ordre partiel. Par consequent, les algorithmes existants n'ont
pas reussi a generer les bases generiques de regles d'association.
Pour remedier aux insuffisances enumerees, nous proposons,
dans ce memoire, un nouvel algorithme, appele PRINCE, permettant l'extraction
des itemsets fermes frequents, leurs generateurs minimaux associes ainsi que
les bases generiques de regles d'association. A cet effet, l'algorithme propose
permet la construction de l'ordre partiel. L'algorithme PRINCE effectue une
exploration par niveau de l'espace de recherche. Sa principale originalite est
qu'il est le seul a construire la relation d'ordre partiel dans l'objectif
d'extraire les bases
generiques de regles. Pour reduire le coUt de cette
construction, la relation d'ordre partiel est maintenue entre l'ensemble des
generateurs minimaux des itemsets fermes frequents et non plus entre les
itemsets fermes frequents. Ceci evite le coUt du calcul des fermetures des
itemsets. Une fois la structure partiellement ordonnee construite, l'extraction
des bases generiques devient immediate.
Structure du memoire
Les resultats de nos travaux de recherche sont synthetises dans
ce memoire qui est compose de quatre chapitres.
Le premier chapitre introduit la technique d'extraction des
regles d'association ainsi que les fondements mathematiques de l'analyse
formelle de concepts. Il definit egalement la connexion de ces fondements avec
le processus d'extraction des bases generiques de regles d'association.
Le deuxieme chapitre presente des algorithmes d'extraction des
itemsets fermes frequents. Ensuite, il presente une etude comparative critique
de ces algorithmes selon des criteres que nous introduisons.
Le troisieme chapitre est consacre a la presentation de
l'algorithme que nous proposons pour l'extraction des trois composantes
permettant la derivation des bases generiques de regles d'association. La
presentation des differentes etapes de l'algorithme PRINCE est donnee. La
demonstration de la validite, la completude et la terminaison ainsi que l'etude
de la complexite theorique de l'algorithme PRINCE seront aussi presentees.
Le quatrieme chapitre presente les experimentations effectuees
sur l'algorithme PRINCE. Ces experimentations sont divisees en deux parties. La
premiere partie s'interesse a l'analyse de quelques optimisations apportees a
notre algorithme ainsi qu'a l'analyse de ses caracteristiques. La deuxieme
partie compare les performances de l'algorithme PRINCE a celles des algorithmes
CLOSE, A-CLOSE et TITANIC.
Chapitre 1
Fondements mathematiques pour
l'extraction de regles d'association
1.1 Introduction
Avec le développement des outils informatiques, nous
avons assisté ces dernières années a un véritable
déluge d'informations stockées dans de grandes bases de
données scientifiques, économiques, financières,
médicales, etc [42]. Le besoin d'interpréter et d'analyser ces
grandes masses de données a suscité beaucoup
d'intérêt. Ainsi, la mise au point de nouvelles techniques
d'analyse est devenue un réel défi pour la communauté
scientifique. Pour répondre a cette pénurie de connaissances sur
les données, de nouvelles méthodes d'extraction de l'information
ont vu le jour, regroupées sous le terme générique de
fouille de données [11]. La fouille de données est un domaine de
recherche en plein essor visant a exploiter les grandes quantités de
données collectées dans divers domaines d'application de
l'informatique. Ce domaine pluri-disciplinaire se situe au confluent de
différents domaines, tels que les statistiques, les bases de
données, l'algorithmique, les mathématiques, l'intelligence
artificielle, etc [54]. On lui donne d'autres appellations, comme par exemple
extraction de connaissances dans les bases de données, traitement de
motifs de données ou encore exploration de données [54]. Selon
Frawley et al. [25] : L'Extraction de Connaissances dans les Bases de
Données (ou Knowledge Discovery in Databases)
désigne le processus interactif et itératif non trivial
d'extraction de connaissances implicites, précédemment inconnues
et potentiellement utiles a partir de données stockées dans les
bases de données.
Ce domaine de recherche a commencé a être
distingué en 1989, quand G. Piatetsky-
Shapiro a organisé la premiere réunion de
chercheurs et d'utilisateurs sur l'extraction automatique de connaissances dans
les grandes bases de données. Une autre étape marquante a
été la création du projet QUEST par IBM en 1993, source de
nombreux algorithmes et méthodes [4].
L'idée sous-jacente de la fouille de données est
donc d'extraire les connaissances cachées A partir d'un ensemble de
données. Le terme fouille de données regroupe un certain nombre
de tAches, telles que la prédiction, le regroupement par similitude, la
classification, l'analyse des clusters, etc [11]. Ces tAches sont elles
mêmes divisées en plusieurs techniques, telles que les regles
d'association, les arbres de décisions, les réseaux de neurones,
etc [24, 42].
Dans ce mémoire, nous allons nous intéresser aux
regles d'association [1]. L'extraction des regles d'association est l'un des
principaux problemes de la fouille de données. Ce probleme, introduit
par Agrawal et al. [1], fut développé pour l'analyse de bases de
données de transactions de ventes. Chaque transaction est
constituée d'une liste d'articles achetés, afin d'identifier les
groupes d'articles achetés le plus fréquemment ensemble [47].
L'analyse d'associations, appliquée aux données des points de
vente, est alors appelée analyse du panier de la ménagère.
L'analyse des associations part des données les plus fines qui composent
une transaction : les ventes des articles élémentaires. La
recherche des associations vise alors a retrouver les corrélations qui
pourraient exister entre n produits (par exemple, les acheteurs de
salade et de tomates achetent de l'huile dans 80% des cas), mais aussi entre
les comportements de produits (quand les ventes de X augmentent alors
les ventes de Y augmentent dans 80% des cas) [42]. L'extraction de
regles d'association a donc pour intérêt l'identification de
corrélations significatives, cachées entre les données
d'une base de données. Les corrélations obtenues peuvent
être utiles pour les utilisateurs finaux (experts, décideurs,
etc.) qui peuvent les exploiter pour différents objectifs.
Dans ce chapitre, nous allons présenter la
problématique d'extraction des regles d'association basée sur les
itemsets fréquents. Ensuite, nous allons présenter les fondements
mathématiques de l'analyse formelle de concepts et leur connexion avec
la dérivation de bases génériques de regles
d'association.
1.2 Derivation des regles d'association
1.2.1 Base de transactions
Une base de transactions peut etre formellement representee
sous la forme d'un triplet K = (O,I,R) dans lequel O
et I sont, respectivement, des ensembles finis d'objets (les
transactions) et d'attributs (les items) et R ? O × I est une
relation binaire entre les transactions et les items. Un couple
(o,i) ? R denote le fait que la transaction o ?
O contient l'item i ? I.
Une transaction T, avec un identificateur appele TID
(Tuple IDentifier), contient un ensemble, non vide, d'items de I. Un
sous-ensemble X de I ou k = |X| est appele
un k-itemset ou simplement un itemset, et k represente la
longueur de X. Le nombre de transactions de K contenant un
itemset X, |{T ? K | X ? T }|, est appele
support absolu de X. Le support relatif de X est le
quotient de son support absolu par le nombre
1IX.
total de transactions de K, cad Supp(X)
{TEK
= Un itemset X est dit frequent
|O| cni
si son support relatif est superieur ou egal a un seuil minimum
minsup(1) specifie par l'utilisateur.
1.2.2 Regles d'association
La formalisation du probleme d'extraction des regles
d'association a ete introduite par Agrawal et al. en 1993 [1]. Une regle
d'association r est une relation entre itemsets de la forme r
: X (Y-X), dans laquelle X et Y sont des
itemsets frequents, tel que X ? Y . Les itemsets X et (Y
-X) sont appeles, respectivement, premisse et conclusion de la
regle r. La generation des regles d'association est realisee a partir
d'un ensemble F d'itemsets frequents dans un contexte d'extraction
K, pour un seuil minimal de support minsup. Les regles d'association
valides sont celles dont la mesure de confiance, Conf(r) =
SSuuppp*(Y
X , est superieure ou egale a un seuil minimal de confiance, defini par
l'utilisateur et qui sera note dans la suite minconf. Si Conf(r) = 1
alors r est appelee regle d'association exacte, sinon elle
est appelee regle d'association approximative [50].
Ainsi, chaque regle d'association, X (Y
-X), est caracterisee par :
1. Le niveau de support : il correspond au nombre de fois oft
l'association est presente, rapporte au nombre de transactions comportant
l'ensemble des items de Y.
Le niveau de support permet de mesurer la frequence de
l'association [42].
2. Le niveau de confiance : il correspond au nombre de fois
oft l'association est presente, rapporte au nombre de presences de X.
Le niveau de confiance permet de mesurer la force de l'association [42].
Ainsi, etant donne un contexte d'extraction /C, le probleme de
l'extraction des regles d'association dans 1C consiste a determiner
l'ensemble des regles d'association dont le support et la confiance sont au
moins egaux respectivement a minsup et minconf. Ce probleme peut etre decompose
en deux sous-problemes comme suit [1] :
1. Determiner l'ensemble des itemsets frequents dans /C, cad les
itemsets dont le support est superieur ou egal a minsup.
2. Pour chaque itemset frequent Ii, generer
toutes les regles d'association de la forme r : I, = I, tel
que I, C I, et dont la confiance est superieure ou egale a minconf.
Ces deux problemes sont resolus par un algorithme fondamental
dans la fouille de donnees, a savoir APRIORI [2]. Le premier sous-probleme a
une complexite exponentielle en fonction du nombre d'itemsets. En effet, etant
donne un ensemble d'items de taille n, le nombre d'itemsets frequents
potentiels est egal a 2'. Le deuxieme sous-probleme est exponentiel en la
taille des itemsets frequents. En effet, pour un itemset frequent I,
le nombre de regles d'association non triviales qui peuvent etre generees est
2|I| - 1. Toutefois, la generation des regles d'association
a partir des itemsets frequents ne necessite aucun balayage de la base de
donnees et les temps de calcul de cette generation sont faibles compares aux
temps necessaires pour la decouverte des itemsets frequents [47]. Neanmoins, le
probleme de la pertinence et de l'utilite des regles extraites est d'une
premiere importance etant donne que dans la plupart des bases de transactions
reelles, des milliers et meme des millions de regles d'association sont
generees [56, 67]. Or, il a ete constate que dans la pratique, plusieurs regles
etaient redondantes [10].
Afin de resoudre ces deux problemes, cad les temps
d'extraction des itemsets fréquents ainsi que la redondance au niveau
des règles d'association valides, Pasquier et al. [48] ont propose, en
1998, une approche qui consiste a extraire les itemsets fermés frequents
au lieu des itemsets frequents. Cette approche est basee sur le fait que
l'ensemble des itemsets fermes frequents est un ensemble generateur de
l'ensemble des itemsets frequents [47]. L'approche par extraction des itemsets
fermes frequents repose sur les fondements mathematiques de l'analyse formelle
de concepts [66]. La section suivante est consacree a la presentation de ces
fondements.
1.3 Analyse formelle de concepts
1.3.1 Introduction
Une base de donnees, appelee aussi contexte d'extraction ou
d'une maniere generale contexte formel, est generalement representee par une
relation binaire entre un ensemble d'attributs I et un ensemble
d'objet O.
Definition 1 Contexte formel
Un contexte formel est un triplet K =
(O,I,R), decrivant deux ensembles finis O et I et
une relation (d'incidence) binaire, R, entre O et I
tel que R ? O × I. L'ensemble O est habituellement
appele ensemble d'objets (ou transactions) et I est appele
ensemble d'attributs (ou items). Cha que couple
(o,i) ? R designe que l'objet o ? O possede
l'attribut
i ? I (note oRi).
Un exemple de contexte formel K est illustre dans la
figure 1.1, avec O =
{1,2,3,4,5} et
I = {A, B,C, D, E}.
|
A
|
B
|
|
CD
|
E
|
|
1
|
×
|
|
×
|
×
|
|
|
2
|
|
×
|
×
|
|
×
|
|
3
|
×
|
×
|
×
|
|
×
|
|
4
|
|
×
|
|
|
×
|
|
5
|
×
|
×
|
×
|
|
×
|
FIG . 1.1 - Exemple de contexte formel
L'analyse formelle de concepts, introduite par Wille en 1982
[66], traite des concepts formels : un concept formel est un ensemble d'objets,
l'extension, auxquels s'appliquent un ensemble d'attributs, l'intention.
L'analyse formelle de concepts offre alors un outil de classification et
d'analyse, dont la notion centrale est le treillis de concepts. Le treillis de
concepts peut etre vu comme un regroupement conceptuel et hierarchique d'objets
(a travers les extensions du treillis), et interprete comme une representation
de toutes les implications entre les items (a travers les intentions) [58].
L'analyse formelle de concepts permet aussi de reduire
considerablement le nombre de relations entre ensembles d'attributs, en ne
generant que celles considerees comme non redondantes.
Dans ce qui suit, nous allons presenter les elements fondamentaux
de l'analyse formelle de concepts.
1.3.2 Notion d'ordre partiel
- Ensembles ordonnes :
Soit E un ensemble. Un ordre partiel sur l'ensemble
E est une relation binaire = sur les elements de E, tel
que pour x, y, z ? E nous avons les proprietes suivantes [21] :
1. Reflexiyite : x = x
2. Anti-symetrie : x = y et y = x x =
y
3. Transitiyite : x = y et y = z x = z
Un ensemble E dote d'une relation d'ordre =,
note (E,=), est appele ensemble partiellement ordonne
[21].
Soient P et Q deux ensembles partiellement
ordonnes. Nous dirons que P et Q sont ordre-isomorphes,
note P ~= Q, s'il existe une bijection f : P
Q et tel que x = y dans P si et seulement si
f(x) = f(y) dans Q. La bijection
f est ainsi dite ordreisomorphisme [21].
- Relation de couverture :
Soient E un ensemble ordonne (E,=
) et x, y deux elements de E. La relation de
couverture entre les elements de E, notee ?, est definie
par x ? y si et seulement si x = y et tel qu'il n'existe pas
d'element z ? E tel que x = z = y pour z =~
x et z =~ y.
Si x ? y, nous disons que y couvre x
ou bien que y est un successeur immediat de x (et donc
x est couvert par y ou x est un predecesseur immediat
de y) [21].
- Join et Meet :
Soit un sous-ensemble S ? E de l'ensemble partiellement
ordonne (E,=). Un element
u ? E est un majorant, ou borne-sup, de S si
pour tout element s ? S, nous avons s = u. L'ensemble des
majorants de S est note UB(S). D'une maniere duale, un element
ü ? E est un minorant, ou borne-inf, de S
si pour tout element s ? S, nous avons v = s.
L'ensemble des minorants de S est note LB(S) [27].
UB(S) = {u ? E | ?s ? S, s =
u}
LB(S) = {v ? E | ?s ? S, v = s}
Le plus petit majorant d'un ensemble S, s'il existe,
est le plus petit element de l'ensemble UB(S) des majorants
de S. Cet element est note Join(S) (?S). D'une
maniere duale, le plus grand minorant d'un ensemble S, s'il existe,
est le plus grand element de l'ensemble LB(S) des minorants
de S. Cet element est note Meet(S) (?S) [27].
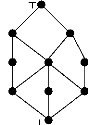
h i
e
a b
c
f g
FIG . 1.2 -- Join - Meet
Exemple 1 Soit le treillis de concepts illustre par la figure
1.2. Ainsi, nous avons : UB({a,b}) = {T, h,i, f}
LB({e, f}) = {a, ?}
- Treillis complet : Un ensemble partiellement ordonne
(E,=) non vide est un treillis si pour tout couple d'elements
(x, y) ? E, l'ensemble {x, y} possede un plus petit
majorant, note x ? y, et un plus grand minorant, note x ?
y.
L'ensemble partiellement ordonne (E,=) est un
treillis complet si pour tout sous-ensemble S ?E, les elements
Join(S) et Meet(S) existent [21].
Les treillis sont frequemment representes sous forme d'un
diagramme de Hasse (les arcs transitifs sont omis), appele egalement graphe de
couverture [21]. Dans ce type de graphe, les sommets correspondent aux elements
de l'ensemble E et les arcs aux relations de couverture entre les sommets
[21].
Theoreme 1 Theoreme fondamental de l'analyse formelle de
concepts [27] : L'ensemble des concepts formels, extrait a partir d'un
contexte formel, constitue un treillis complet quand les concepts
formels sont ordonnes par inclusion des extensions (ou par inclusion
des intentions).
- Join-irreductible et Meet-irreductible :
Pour un element l d'un treillis complet L, nous
definissons [21] :
l* = ?{x ? L|x <
l}
l* = ?{x ? L|l < x}
Un element l est dit Join-irreductible s'il couvre un
element unique. D'une maniere duale, l est dit Meet-irreductible, s'il
est couvert par un seul element.
L'ensemble des elements Join-irreductible de L est
note par J (L) et l'ensemble des elements Meet-irreductible
de L est note par M(L). Chacun de ces ensembles
herite de la relation d'ordre de L [21].
Exemple 2 Dans la figure 1.2, b est un element
Meet-irreductible, alors que e est un
element
Join-irreductible. Dans la figure 1.3, nous avons J(L) =
{b, c} et M(L) = {e, f}.

b c
a
d
e f
FIG 1.3 -- Join-irreductible - Meet-irreductible
1.3.3 Connexion de Galois
- Operateurs de fermeture :
Soit un ensemble partiellement ordonne
(E,=). Une application ã de
(E,=) dans (E,=) est appelee un
operateur de fermeture, si et seulement si elle possede les proprietes
suivantes. Pour tout sous-ensemble S, S' ? E [21] :
1. Isotonie : S = S' ã(S) ?
ã(S')
2. Extensivite : S ? ã(S)
3. Idempotence :
ã(ã(S)) = ã(S)
Etant donne un operateur de fermeture ã sur un
ensemble partiellement ordonne (E,=), un element
x ? E est un element ferme si l'image de x par l'operateur de
fermeture ã est egale a lui-même, cad
ã(x) = x [21].
- Connexion de Galois :
Soit un contexte d'extraction K =
~O,I,R~. Soit l'application ö, de
l'ensemble des parties de OM dans l'ensemble des parties de
I, qui associe a un ensemble d'objets O ? O l'ensemble des
items i ? I communs a tous les objets o ? O [27] :
ö : 2O ?
2I
ö(O) = {i ? I|?o ? O ? oRi }
Soit l'application ø, de l'ensemble des
parties de I dans l'ensemble des parties de O, qui
associe a tout ensemble d'items (communement appele itemset) I ? I
l'ensemble des objets o ? O contenant tous les items i ? I
[27] :
ø : 2I ?
2O
ø(I) = {o ? O|?i ? I ? oRi
}
Le couple d'applications (ö,ø)
est une connexion de Galois entre l'ensemble des parties de O et
l'ensemble des parties de I [3, 27]. Etant donne une connexion de
Galois, les proprietes suivantes sont verifiees quelques soient I,
I1, I2 ? I et O,
O1, O2 ? O [27] :
1. I1 ? I2
ø(I2) ?
ø(I1);
2. O1 ? O2
ö(O2) ? ö(O1)
;
3. O ? ø(I) ? I ?
ö(O) ? (I,O) ? R.
- Fermeture de la connexion de Galois :
Nous considerons les ensembles des parties
2I et 2O dotes de la relation
d'inclusion ?, cad les ensembles partiellement ordonnes
(2I, ? ) et (2O, ? ).
Les operateurs ã = ö ? ø de
(2I, ? ) dans (2I, ?
) et ã'= ø ? ö de
(2O, ? ) dans (2O, ?
) sont des operateurs de fermeture de la connexion de Galois [3, 27].
Etant donne une connexion de Galois, les proprietes suivantes sont verifiees
quelques soient I, I1, I2
? I et O, O1, O2 ?
O [27] :
1. I ? ã(I) 1'. O ?
ã'(O)
2.
ã(ã(I))=ã(I)
2'.
ã'(ã'(O))=ã~(O)
3. I1 ? I2
ã(I1) ?
ã(I2) 3'. O1 ?
O2 ã'(O1) ?
ã'(O2)
4. ã(ø(I)) =
ø(I) 4'. ã(ö(O))
= ö(O)
- Treillis de concepts formels (de Galois) :
Etant donne un contexte d'extraction
K=(O,I,R), l'ensemble de concepts formels
CK est un treillis complet LC,, = (CK, =),
appele treillis de concepts formels (de Galois), quand l'ensemble
CK est considere avec la relation d'inclusion entre les itemsets [3, 27].
La relation d'ordre partiel entre des concepts formels est definie comme suit
[27] : ? c1=
(O1,I1), c2
=(O2,I2) ? CK,
c1 = c2 ? I2 ?
I1 (? O1 ? O2) avec
I1, I2 ? I et
O1, O2 ? O.
Dans un treillis de concepts, l'element
ø(O) x O est appele element Bottom du
treillis (note 1) et l'element Z x
ö(Z) est appele element Top du treillis (note T).
Le chemin amenant du Bottom jusqu'au Top est appele chaine maximale du treillis
[27].
Dans un treillis de concepts, les operateurs Join et Meet
permettent d'obtenir, respectivement, la plus petite borne superieure et la
plus grande borne inferieure. Les operateurs Join et Meet sont definis comme
suit [27] :
V O1, O2 C O
et I1, I2 C Z :
- (O1, I1) V
(O2, I2) =
(ã(O1 U O2),
I1 n I2),
- (O1, I1) A
(O2, I2 = (O1 n
O2, ã(I1 U
I2)).
La relation d'ordre partiel est utilisee pour generer le graphe
du treillis, appele Diagramme de Hasse, comme suit [27] :
Il existe un arc (c1, c2), si
c1 c2 oft est la reduction transitive de <,
cad Vc3 E CK,
c1 < c3 < c2
c1 =c3 ou c2 =c3.
Dans ce graphe, les sommets correspondent aux elements de
l'ensemble Ck et les arcs aux relations de couverture entre les
sommets. Chaque element c E Cic est connecte aussi bien a un
ensemble de ses successeurs immediats, appele Couverture superieure
(Couvs), et a un ensemble de ses predecesseurs
immediats, appele Couverture inferieure (Couvi).
1.3.4 Itemsets fermes et leurs generateurs minimaux
Dans cette section, nous definissons :
G les itemsets fermes qui peuvent être ordonnes sous la
forme d'un treillis des itemsets fermes.
G les itemsets fermes frequents qui peuvent être ordonne
sous la forme d'un treillis d'Iceberg.
les generateurs minimaux.
- Itemset ferme :
Etant donne l'operateur de fermeture de la connexion de
Galois ã, un itemset l C Z tel que
ã(l) = l est appele itemset ferme. Un itemset
ferme est donc un ensemble maximal d'items communs a un ensemble d'objets
[47].
[BC} n'est pas un itemset ferme car il n'est pas un ensemble
maximal d'items communs a certains objets : tous les objets contenant
les items B et C, cad les objets 2,3 et 5 contiennent egalement l'item
E.
- Ensemble d'itemsets fermes :
Soit un contexte d'extraction K =
(O,I,R) et l'operateur de fermeture de la connexion
de Galois ã. L'ensemble IF des itemsets fermes dans le
contexte K est defini comme suit [47] :
IF = {l ? I 1 l= Ø ?
ã(l~=lP.
Le plus petit (minimal au sens de l'inclusion) itemset ferme
contenant un itemset l est obtenu par l'application de l'operateur
ã a l [47].
- treillis des itemsets fermes :
L'operateur de fermeture ã induit une
relation d'equivalence sur l'ensemble de parties de I, cad l'ensemble
de parties est partionne en des sous-ensembles disjoints, appeles aussi classes
d'equivalence. Dans chaque classe, tous les elements possedent la meme valeur
de support. Les generateurs minimaux d'une classe sont les elements
incomparables (selon la relation d'inclusion) les plus petits, tandis que
l'itemset ferme est l'element le plus large de cette classe. Ces classes
d'equivalence sont ordonnees sous forme d'un treillis de concepts formels (de
Galois) oft chaque concept formel est dans ce cas un itemset ferme. Ainsi, le
couple LIF =-- (IF,?) est un treillis complet appele
treillis des itemsets fermes [47].
- Itemset ferme frequent :
Un itemset ferme l est dit frequent si son support
relatif, Supp(l) = |ø~l~|
|O| ,excede un seuil minimum fixe par l'utilisateur note
minsup [47]. Notons que |ø(l~| est appele
support absolu de l.
Agrawal et al. ont introduit dans [1], les deux proprietes
suivantes relatives aux supports des itemsets frequents :
1. Tous les sous-ensembles d'un itemset frequent sont
frequents.
2. Tous les sur-ensembles d'un itemset infrequent sont
infrequents.
Ces proprietes restent applicables dans le cas des itemsets
fermes frequents [47]. Ainsi,
1. Tous les sous-ensembles d'un itemset ferme frequent sont
frequents.
2. Tous les sur-ensembles d'un itemset ferme infrequent sont
infrequents.
Sachant que le support d'un itemset (frequent) l est
egal au support de sa fermeture ã(l) qui est le plus
petit itemset ferme contenant l : Supp(l) =
Supp(ã(l~) [47].
- Treillis d'Iceberg :
Quand nous considerons seulement l'ensemble des itemsets
fermes frequents ordonnes par la relation d'inclusion ensembliste, la structure
obtenue (àL, ? ) preserve seulement l'operateur
Join. Cette structure forme un semi-treillis superieur et elle est designee par
treillis d'Iceberg [6, 57, 63].
- Generateur minimal :
Un itemset g ? I est dit generateur minimal d'un
itemset ferme f, si et seulement si ã(g)
= f et il n'existe pas g1 ? I tel que
g1 ? g [5]. L'ensemble GMf des generateurs
minimaux d'un itemset ferme f est defini comme suit :
GMf = { g ? I l
ã(g)=f ? l g1 ? g
tel que ã(g1) =f }.
Dans la suite, nous allons montrer la connexion de l'analyse
formelle de concepts avec l'extraction des bases generiques de regles
d'association.
1.4 Derivation des bases generiques de regles
d'association
Depuis l'apparition de l'approche basee sur l'extraction des
itemsets fermes frequents [48], une nouvelle formulation du probleme de
l'extraction des regles d'association est proposee et qui consiste a extraire
les itemsets fermes frequents au lieu des itemsets frequents. Ceci permet [47]
:
D'ameliorer les temps de calcul, puisque dans la plupart des
cas, le nombre d'itemsets fermes frequents est largement inferieur au nombre
d'itemsets frequents, surtout pour les bases de transactions fortement
correlees ou denses.
De generer que des regles d'association non redondantes.
Cette nouvelle approche -- l'extraction des itemsets fermes
frequents -- a donne lieu a une selection de sous-ensembles de regles sans
perte d'information. La selection de regles sans perte d'information repose sur
l'extraction d'un sous-ensemble de toutes les regles
d'association, appele base generi que, a partir duquel le
reste des regles pourrait etre derive. Dans ce memoire, nous allons nous
interesser en particulier a l'approche de Bastide et al. [4, 5]. Cette
approche presente deux bases generiques qui sont definies comme suit :
1. La Base generi que de regles d'association exactes, adaptee
de la base d'implications globales de Guigues et Duquenne [31], est definie
comme suit [4, 5] :
Definition 2 Soit IFFK l'ensemble des itemsets
fermes frequents extrait d'un contexte d'extraction K. Pour
cha que itemset ferme frequent f ? IFFK, nous designons par GMf
l'ensemble de ses generateurs minimaux. La base generi que de regles
d'association exactes est donnee par : BG = {R :
g (f - g) | f ? IFFK et g ? GMf
et g f(3)}
2.
.
La base generique de regles d'association approximatives
appelee Base informative de regles d'association approximatives,
adaptee de la base d'implications partielles de Luxenburger [45], est definie
comme suit [4, 5] :
Definition 3 Soit GMFK l'ensemble des generateurs
minimaux frequents extrait d'un contexte d'extraction K. La
base informative de regles d'association approximatives BI est donnee
par : BI = {R : g (f - g) | f
? IFFK et g ? GMFK et ã(g) ? f
et Conf (R) = minconf}.
Afin de reduire le nombre de regles generiques approximatives,
Bastide et al. proposent une reduction transitive de la base informative [4,
5], qui est elle-meme une base pour toutes les regles approximatives, definie
de la maniere suivante :
Definition 4 La reduction transitive RI de la base
informative est donnee par : RI {R : g (f
- g) | f ? IFFK et g ? GMFK et
ã(g) ? f et Conf (R) =
minconf}.
Ainsi, il est possible de determiner toutes les regles de la
base informative et donc toutes les regles approximatives a partir de la
reduction transitive [4, 5]. Ceci a pour avantage de presenter un ensemble
minimal de regles a l'utilisateur, ce qui lui permet de mieux les visualiser et
les utiliser.
Dans la suite, nous allons considerer les regles d'association
generiques formees par l'union de la base generique de regles exactes et la
reduction transitive de la base informative. Ces regles seront designees par
regles d'association informatives. Ainsi, etant donne un treillis d'Iceberg,
dans lequel chaque itemset ferme frequent est decore par sa liste de
generateurs minimaux, la derivation de ces regles peut se faire d'une maniere
directe. En
3La condition g 0 f permet de ne pas
retenir les regles de la forme g Ø.
effet, les regles approximatives génériques sont
des implications "inter-nceuds" assorties d'une mesure de confiance. Cette
implication met en jeu deux classes d'équivalence comparables, cad d'un
itemset fermé vers un autre itemset fermé le couvrant
immédiatement dans la structure partiellement ordonnée. En
revanche, les regles génériques exactes sont des implications
"intra-nceud", avec une confiance égale a 1, extraites de chaque nceud
dans la structure partiellement ordonnée.
Il faut noter que les bases considérées
présentent plusieurs avantages [4, 5, 41] :
1. Ces bases donnent des regles génériques avec
un nombre minimal d'items dans la prémisse et un nombre maximal d'items
dans la conclusion [38]. Ceci donne les regles les plus informatives pour
l'utilisateur [47].
2. Ces bases n'induisent aucune perte d'information. En
effet, ces bases génériques présentent un ensemble minimal
de regles, a partir duquel toutes les regles valides peuvent etre
retrouvées par application d'axiomes d'inférence comme ceux
proposés dans [10]. En plus, ces bases sont informatives, cad qu'elles
permettent de retrouver, pour chaque regle redondante, son support et sa
confiance sans acces au contexte d'extraction.
3. Ces bases sont valides, cad qu'elles ne permettent de
générer que les regles redondantes ayant un support et une
confiance dépassant respectivement minsup et minconf.
4. La réduction transitive regroupe les regles
approximatives génériques ayant des confiances
élevées. En effet, chacune des regles, formant la
réduction transitive, constitue un lien entre deux classes
d'équivalence dont l'une couvre l'autre immédiatement. Ces
classes d'équivalence ont généralement des supports
proches. Ceci permet d'avoir des regles d'association présentant des
confiances élevées. Sauf rares exceptions, ces regles sont les
plus intéressantes [4].
Les algorithmes présentés dans [5, 47]
permettent d'extraire ces bases en supposant l'existence des itemsets
fermés fréquents ainsi que leurs générateurs
minimaux respectifs. Ceci nécessite l'application en amont d'un autre
algorithme tel que CLOSE [48, 49] ou A-CLOSE [50], etc. La
génération de la base générique de regles
d'association exactes se fait alors d'une maniere directe. Cependant pour les
regles d'association approximatives, des tests d'inclusion coitteux, mettant en
jeu les itemsets fermés fréquents, sont réalisés
pour déterminer les successeurs immédiats de chaque classe
d'équivalence.
1.5 Conclusion
Un problème classique de la fouille de données
est la recherche de regles d'association dans les données, introduit par
Agrawal et al. [1]. Etant donné, le nombre élevé
d'itemsets fréquents et donc le nombre élevé des regles
d'association (redondantes) extraites même dans le cas de contextes
d'extraction de petites tailles, une nouvelle approche préconisant
l'extraction des itemsets fermés fréquents [48], a vu le jour.
Cette approche vise a réduire le cotit de l'extraction des itemsets
fréquents et surtout a ne générer qu'un sous-ensemble
généri que de l'ensemble de toutes les regles d'association. Dans
le chapitre suivant, nous allons présenter les principaux algorithmes
permettant l'extraction des itemsets fermés fréquents.
Chapitre 2
Algorithmes d'extraction des itemsets
fermes frequents : Etat de l'art
2.1 Introduction
L'extraction des regles d'association est l'une des techniques
les plus importantes dans le domaine de la fouille de données [11]. La
premiere approche d'extraction des regles d'association s'est basée sur
la découverte des itemsets fréquents [2]. Cependant, cette
approche souffre de deux problemes majeurs, a savoir le coit de l'extraction
des itemsets fréquents a partir desquels seront extraites de grandes
quantités de regles d'association. Cette quantité énorme
de connaissance rend quasi impossible leur analyse par un expert humain. Pour
pallier ces inconvénients, une nouvelle approche basée sur
l'extraction des itemsets fermés fréquents [48] est apparue.
Cette approche exploitant les fondements mathématiques de l'analyse
formelle de concepts [66], propose de réduire le coit de l'extraction
des itemsets fréquents en se basant sur le fait que l'ensemble des
itemsets fermés fréquents est un ensemble
générateur de l'ensemble des itemsets fréquents [48]. En
outre, elle propose une sélection, sans perte d'information, d'un
sous-ensemble de toutes les regles d'association, appelé base
générigue, a partir duquel le reste des regles pourrait etre
dérivé [48]. Cette approche permet de réduire le nombre de
regles extraites en ne gardant que les plus intéressantes pour
l'utilisateur et lui donne la possibilité de mieux les visualiser et les
exploiter.
2.2 Algorithmes d'extraction des itemsets fermes
frequents
La premiere approche d'extraction des regles d'association
s'est basee sur l'extraction des itemsets frequents. Les algorithmes, adoptant
cette approche, peuvent etre classes suivant les strategies d'exploration
utilisees pour traverser le treillis des itemsets : en largeur d'abord [2], en
profondeur d'abord [34] ou une strategie hybride [70]. En adoptant une
strategie en largeur d'abord, tous les k-itemsets candidats sont
generes en faisant une auto-jointure de l'ensemble des (k-1)-itemsets
frequents [2]. Quand une strategie en profondeur d'abord est adoptee, etant
donne un (k-1)-itemset frequent X, les k-itemsets
candidats sont generes en ajoutant un item i, i/?X, a
X. Si {X U i} est aussi frequent, le processus est
repete recursivement pour {X U i} [34]. La troisieme
strategie explore en profondeur d'abord le treillis des itemsets, mais ne
genere qu'un seul itemset a la fois [70].
Afin de resoudre les problemes rencontres par les algorithmes
d'extraction des itemsets frequents, une nouvelle approche basee sur
l'extraction des itemsets fermes frequents est apparue. Cette approche est
basee sur la fermeture de la connexion de Galois [27] pour resoudre le probleme
d'extraction de regles d'association [48]. Elle est fondee sur un elagage du
treillis des itemsets fermes, en utilisant les operateurs de fermeture de la
connexion de Galois [27]. Plusieurs algorithmes ont ete proposes dans la
litterature [49, 50, 51, 57, 69], dont le but est de decouvrir les itemsets
fermes frequents.
Quand nous nous interessons a l'extraction des itemsets fermes
frequents seulement, la generation des candidats et la verification s'ils sont
fermes ou non, ne peuvent pas etre directement appliquees contrairement aux
algorithmes permettant de determiner les itemsets frequents [43]. En effet, il
n'est pas possible de generer des itemsets fermes candidats en faisant une
auto-jointure des itemsets fermes dejà decouverts. Par exemple, etant
donne un itemset ferme X, il peut arriver qu'aucun des sur-ensembles
de X, obtenus en etendant X par un seul item, ne soit un
ferme [43].
Etant donne le fait que les candidats fermes frequents ne
peuvent pas etre generes directement, tous les algorithmes, permettant de
trouver les itemsets fermes frequent, sont bases sur deux etapes qui
co-existent. La premiere etape consiste a naviguer dans l'espace de recherche
en traversant le treillis des itemsets frequents d'une classe d'equivalence a
une autre. Durant la deuxieme etape, ces algorithmes calculent les fermetures
des itemsets
frequents visites, dans le but de determiner les itemsets fermes
frequents de la classe d'equivalence correspondante [43].
Ainsi, nous proposons que les strategies adoptees pour
l'exploration de l'espace de recherche soient decomposees en trois strategies,
a savoir "Generer-et-tester", "Diyiser-etgenerer" et une strategie hybride :
1. La strategie "Generer-et-tester" : les algorithmes
adoptant cette strategie parcourent l'espace de recherche par niveau. A chaque
niveau k, un ensemble de candidats de taille k est genere.
Cet ensemble de candidats est, generalement, elague par la conjonction d'une
metrique statistique (cad le support) et des heuristiques basees
essentiellement sur les proprietes structurelles des itemsets fermes et/ou des
generateurs minimaux [9].
2. La strategie "Diviser-et-generer" : les algorithmes
adoptant cette strategie essaient de diviser le contexte d'extraction en des
sous-contextes et d'appliquer le processus de decouverte des itemsets fermes
recursivement sur ces sous-contextes. Ce processus de decouverte repose sur un
elagage du contexte base essentiellement sur l'utilisation d'une metrique
statistique et d'heuristiques introduites [9].
3. La strategie hybride : les algorithmes adoptant cette
strategie utilisent les proprietes des deux strategies precedentes. Ils
explorent l'espace de recherche en profondeur d'abord (tel que les algorithmes
de la strategie "Diyiser-et-generer") mais sans diviser le contexte
d'extraction en des sous-contextes. Ces algorithmes genèrent un ensemble
de candidats tel que c'est le cas dans la strategie "Generer-et-tester".
Cependant, cet ensemble est toujours reduit a un seul element. Ces algorithmes
essaient alors de verifier si ce candidat est un itemset ferme frequent ou non.
Le processus d'extraction se base aussi sur des strategies d'elagage [69]. Ces
derniers consistent a utiliser une metrique statistique en conjonction avec
d'autres heuristiques.
Dans la suite, nous allons passer en revue les principaux
algorithmes permettant l'extraction des itemsets fermes frequents en les
distinguant par rapport a la strategie d'exploration etant donne que c'est le
critère utilise dans la litterature [9, 36].
2.2.1 Les algorithmes de type
!,Générer-et-tester!,
Dans cette sous section, nous allons passer en revue les
algorithmes les plus connus operant selon la strategie "Generer-et-tester". Une
structure generale d'un algorithme entrant dans cette categorie est presentee
dans [9].
Chacun des algorithmes, que nous allons presenter dans la
suite, est caracterise par une phase d'elagage et par une phase de
construction. Lors de la phase d'elagage et en plus de l'elagage des candidats
infrequents, cad ayant un support strictement inferieur a minsup, chaque
algorithme introduit de nouvelles strategies d'elagage pour essayer de reduire
le coUt supplementaire du calcul des fermetures des itemsets [9]. Notons que
ces strategies dependent de l'information dont dispose l'algorithme. Cette
information peut être soit l'ensemble des generateurs minimaux seuls,
soit accompagne de l'ensemble des itemsets fermes [9]. La phase de construction
relative a une iteration k, permet de generer les candidats de
taille k a partir de ceux retenus lors de l'iteration (k-1)
(cad de taille (k-1)).
Une methode d'elagage commune aux algorithmes adoptant la
strategie "Generer-ettester" se base sur la verification de l'ideal d'ordre des
generateurs minimaux frequents. Cette notion est definie comme suit :
Proposition 1 [55, 571 L'ensemble GMFK des
generateurs minimaux frequents extraits d'un contexte d'extraction
K verifie la propriete de l'ordre ideal de
(P(I),? ), cad si g ? GMFK et
g1 ? g alors g1 ? GMFK,
pour tout g, g1 ? I.
La definition d'un ordre ideal des generateurs minimaux frequents
est equivalente a : g1 ?/ GMFK,
g1 ? g g ?/ GMFK, pour tout g,
g1 ? I.
Definition 5 [55, 571 Soit GMFK un ordre ideal de
(P(I),? ). Un itemset candidat g pour
GMFK est un sous-ensemble de I tel que tous ses sous-ensembles
sont des generateurs minimaux frequents.
Ainsi, tout candidat generateur minimal frequent g de
taille k, est elague dans le cas oft un de ses sous-ensembles n'est
pas un generateur minimal frequent.
2.2.1.1 L'algorithme CLOSE
L'algorithme CLOSE propose par Pasquier et al. [48, 49] est le
premier algorithme permettant l'extraction des itemsets fermes frequents. Cet
algorithme se base sur les generateurs minimaux pour calculer les itemsets
fermes. Ces generateurs minimaux sont utilises pour construire un ensemble
d'itemsets fermes candidats (itemsets fermes potentiellement frequents), qui
sont les fermetures des generateurs minimaux. Ainsi, etant donne un contexte
d'extraction K, CLOSE genere toutes les regles d'association en trois
etapes successives [9] :
1. Decouverte des itemsets fermes frequents ;
2. Derivation de tous les itemsets frequents a partir des
itemsets fermes frequents obtenus durant la premiere etape ;
3. Pour chaque itemset frequent, generation de toutes les regles
ayant une confiance au moins egale a minconf.
L'algorithme CLOSE parcourt l'ensemble des generateurs
minimaux des itemsets fermes frequents par niveaux. L'ensemble d'itemsets
fermes frequents candidats d'une iteration k est l'ensemble des
fermetures des k-generateurs minimaux frequents de cette iteration.
Durant la premiere iteration, l'ensemble des 1-generateurs minimaux est
initialise avec la liste des 1-itemsets du contexte d'extraction, tries par
ordre lexicographique. CLOSE calcule alors le support et la fermeture de ces
generateurs moyennant un acces au contexte d'extraction. Les generateurs
minimaux infrequents et leurs fermetures sont alors elimines. Ensuite, pour
chaque iteration k, CLOSE construit un ensemble de candidats
generateurs minimaux frequents de taille k en utilisant la phase
combinatoire d'APRiORi-GEN [2] appliquee aux (k-1)-generateurs
minimaux frequents retenus lors de l'iteration precedente. De cet ensemble est
elague tout candidat ne verifiant pas l'ideal d'ordre des generateurs minimaux
frequents ou s'il est inclus dans la fermeture d'un de ses sous-ensembles de
taille (k-1), calculee lors de l'iteration precedente [48, 49]. Une
fois ces tests d'elagage effectues, CLOSE accede au contexte d'extraction pour
calculer le support et la fermeture des candidats retenus. Pour calculer la
fermeture des candidats, CLOSE utilise la fonction GEN-CLOSURE [48, 49]. Cette
fonction determine, pour chaque transaction T du contexte
d'extraction, les generateurs minimaux qui sont inclus dans T. Pour
chacun de ces generateurs minimaux, GEN-CLOSURE calcule sa fermeture et
incremente son support. La fermeture est egale a l'intersection de T
avec l'ancienne valeur de la fermeture, si cette derniere est non nulle sinon
la nouvelle valeur est egale a T. Une fois l'acces au contexte
d'extraction termine, CLOSE ne retient que les fermetures des generateurs
minimaux qui sont frequents. Ainsi, les candidats infrequents, et pour lesquels
le calcul de la fermeture est logiquement non necessaire, sont elimines.
L'execution de l'algorithme CLOSE prend fin quand il n'y plus de candidats a
generer.
Etant donne que dans chaque iteration, le calcul des supports
et des fermetures des candidats est l'etape la plus exigeante en temps
d'execution, CLOSE utilise une structure de donnees avancee basee sur la notion
d'arbre prefixe (ou trie(')) derivee de celle proposee
'Le mot trie est inspire du mot anglais reTRIEval.
par Mueller dans [46]. Dans cette structure, chaque candidat
est represente par un chemin de la racine a une feuille du trie. La fermeture
de chaque candidat est stockee au niveau de la feuille le representant dans le
trie. A la fin de chaque iteration, les generateurs minimaux frequents, leurs
supports et leurs fermetures sont stockes dans un autre trie ayant la
meme structure que celui utilise pour le calcul des supports et des fermetures.
Le fait d'utiliser un trie pour chaque ensemble de generateurs minimaux
frequents, d'une taille k donnee, necessite une grande quantite
d'espace memoire (etant donne qu'il y a beaucoup de redondance).
CLOSE necessite au pire des cas acces au contexte d'extraction
(TIT etant la taille
maximale possible d'un generateur minimal).
2.2.1.2 L'algorithme A-CLOSE
L'algorithme A-CLOSE, propose par Pasquier et al. [50], permet
l'extraction des itemsets fermes frequents en utilisant les proprietes des
supports des generateurs minimaux des itemsets fermes frequents. L'amelioration
apportee a l'algorithme A-CLOSE par rapport a l'algorithme CLOSE, reside dans
le fait que A-CLOSE, apres avoir construit un ensemble de
k-generateurs candidats a partir des (k-1)-generateurs minimaux
retenus dans la (k1)i`eme iteration, supprime de cet
ensemble tout candidat g dont le support est egal au support d'un de
ses sous-ensembles de taille (k-1) [50].
Ainsi, A-CLOSE procede en deux etapes successives :
1. Il determine tous les generateurs minimaux frequents, cad les
plus petits elements incomparables des classes d'equivalence induites par
l'operateur de fermeture ã.
2. Pour chaque classe d'equivalence, il determine l'element
maximal residant au sommet de la hierarchie, cad l'itemset ferme frequent.
Lors de la premiere etape, A-CLOSE parcourt l'espace de
recherche en largeur d'abord. A-CLOSE initialise alors l'ensemble des
1-generateurs minimaux par les 1-itemsets du contexte d'extraction, tries par
ordre lexicographique. Un acces au contexte d'extraction permet de calculer
seulement le support de ces generateurs (les fermetures ne sont pas calculees).
Ensuite, a chaque iteration k, A-CLOSE construit un ensemble de
k-candidats generateurs minimaux en joignant les generateurs minimaux
frequents retenus lors de l'iteration precedente (cad de taille (k-1))
grace a la phase combinatoire d'APRiORi-GEN [2]. De cet ensemble est elague
tout candidat ne verifiant pas l'ideal d'ordre des generateurs minimaux
frequents. Une fois cet elagage effectue, un acces au contexte d'extraction
est
effectué pour calculer le support des candidats
retenus. Ensuite, A-CLOSE élimine tout candidat g qui se
révèle infréquent ou ayant un support égal a celui
d'un de ses sous-ensembles de taille (k-1) [50]. Afin de
vérifier cette dernière condition, A-CLOSE effectue un balayage
des générateurs minimaux retenus de taille (k-1)
permettant de comparer le support de g avec le support de ses
sous-ensembles de taille (k-1) [50]. La première étape
de l'algorithme A-CLOSE prend fin lorsqu'il n'y a plus de candidats a
générer.
Lors de la deuxième étape, A-CLOSE calcule les
fermetures de tous les générateurs minimaux fréquents
retenus lors de la première étape. A cette fin, A-CLOSE
accède au contexte d'extraction et utilise la fonction AC-CLOSURE [50]
qui est la même que la fonction GEN-CLOSURE utilisée dans
l'algorithme CLOSE amoindrie de la phase du calcul du support [50].
Pour alléger le calcul des fermetures, l'algorithme
A-CLOSE mémorise le numéro de la première itération
durant laquelle un candidat fréquent non générateur
minimal (cad ayant un support égal a celui d'un de ses sous-ensembles) a
été identifié. Le numéro de cette itération
correspond a la taille t de ce candidat. Il n'est alors pas
nécessaire de calculer la fermeture des générateurs
minimaux fréquents de tailles inférieures a (t-1),
puisqu'ils sont tous des itemsets fermés fréquents [50]. En
effet, ils sont eux-mêmes leur propres générateurs uniques
[47].
Comme dans le cas de l'algorithme CLOSE, et pour chaque
itération, A-CLOSE utilise un trie pour accélérer le
calcul du support des candidats et un autre trie pour stocker l'ensemble des
générateurs minimaux fréquents retenus. La fermeture de
chaque générateur minimal fréquent sera
complétée lors de la deuxième étape.
A-CLOSE nécessite au plus (1/1+1) accès au
contexte d'extraction (1/1 étant la taille maximale possible d'un
candidat générateur minimal). Les 1/1 accès sont
nécessaires pour déterminer l'ensemble des
générateurs minimaux fréquents, alors que le dernier
accès permet éventuellement de calculer les fermetures des
générateurs retenus.
2.2.1.3 L'algorithme TITANIC
L'algorithme TITANIC a été proposé par
Stumme et al. [55, 57], pour la découverte des itemsets fermés
fréquents. L'idée clé est de minimiser le coUt du calcul
des fermetures en adoptant un mécanisme de comptage par inférence
[6]. Ainsi, l'algorithme traverse
l'espace de recherche par niveau en focalisant sur la
determination des generateurs minimaux (ou itemsets cles [55, 57]) frequents
des differentes classes d'equivalence induites par l'operateur de fermeture
ã.
Une des particularites de TITANIC est qu'il considere,
contrairement a CLOSE et A-CLOSE, l'ensemble vide (0) comme etant un generateur
minimal. Pour calculer la fermeture de l'ensemble vide, TITANIC collecte les
items de meme support que cet ensemble, cad qui se repetent dans toutes les
transactions. Ainsi, l'ensemble vide est le generateur minimal de support egal
au nombre de transactions du contexte d'extraction (cad 101).
En plus, TITANIC evite le balayage supplementaire (des generateurs
minimaux frequents retenus de taille (k-1)) effectue dans A-CLOSE pour
chaque candidat g de taille k. En effet, TITANIC utilise une
variable dans laquelle il stocke le support estime de g. Ce dernier
est egal au minimum des supports des (k-1)-generateurs minimaux
frequents inclus dans g et il doit etre different du support reel
de g sinon g n'est pas minimal [55, 57].
De meme que CLOSE et A-CLOSE, TITANIC parcourt l'espace de
recherche par niveau. Il initialise l'ensemble des 1-generateurs minimaux par
les 1-itemsets du contexte d'extraction, tries par ordre lexicographique.
TITANIC calcule alors le support de ces itemsets et determine ensuite la
fermeture de l'ensemble vide. Les items infrequents ou ayant le meme support
que l'ensemble vide ne sont pas des generateurs minimaux frequents. Ensuite, a
chaque iteration k, TITANIC genere un ensemble de candidats moyennant
l'utilisation de la phase combinatoire d'APRIORI-GEN [2]. De cet ensemble, sont
elimines les candidats ne verifiant pas l'ideal d'ordre des generateurs
minimaux frequents. Un acces au contexte d'extraction permet de calculer le
support des candidats non elagues. De ces candidats, sont elimines les
generateurs infrequents ou ayant des supports reels egaux a leurs supports
estimes. Une fois les k-generateurs minimaux frequents determines,
TITANIC calcule la fermeture des generateurs minimaux frequents retenus lors de
l'iteration precedente (cad de taille (k-1)). Neanmoins, TITANIC evite
l'acces au contexte d'extraction pour calculer les fermetures et ceci en
adoptant un mecanisme de comptage par inference [6]. Ainsi, pour chaque
(k-1)-generateur minimal frequent g, TITANIC fait appel a la
fonction CLOSURE [55, 57]. Cette derniere se deroule de la maniere suivante
[55, 57] :
1. Pour alleger les calculs, la fermeture de g,
ã(g), serait egale a l'union des fermetures de ses
sous-ensembles de taille (k - 2), calculees lors de l'iteration
precedente.
2. Ensuite, pour tout item frequent i n'appartenant pas
a ã(g) a ce moment du traitement, i est
ajoute a ã(g) si Supp(g U {i}) =
Supp(g). Deux cas sont a distinguer :
(a) Si g ? {i} est un candidat generateur
minimal, le support de g ? {i} est directement determine.
(b) Si g ? {i} n'est pas un candidat
generateur minimal, TITANIC utilise un mecanisme de comptage par inference [6]
permettant de trouver le support de g ? {i} sans acceder au
contexte d'extraction. Ce mecanisme est fonde sur le fait que le support d'un
itemset non generateur minimal peut etre calcule en utilisant l'ensemble des
generateurs minimaux frequents GMFK et la bordure negative des
generateurs minimaux notee GBd- [39]. Cette
dernière est formee par l'ensemble des generateurs minimaux infrequents
dont tous leurs sous-ensembles sont des generateurs minimaux
frequents. TITANIC utilise alors la proposition suivante :
Proposition 2 [55, 571 Soit GMK l'ensemble des
generateurs minimaux ex-traits du contexte K. Si X est un
itemset non generateur minimal alors SuPP(X) > min
{SuPP(g) | g ? GMK et g ? X}.
Pour pouvoir utiliser cette proposition et etant donne que
X peut etre un itemset non frequent, TITANIC est amene a gerer le stockage
de l'ensemble GBd-. En effet, si TITANIC se
contente seulement des generateurs minimaux frequents pour calculer le support
de X, ce support serait egal au minimum des supports des generateurs
minimaux frequents contenus dans X. Ceci contredit le fait que
X pourrait etre infrequent. Ainsi, l'affirmation de Stumme et al. dans
[57] de pouvoir supprimer les generateurs minimaux infrequents est erronee.
L'execution de l'algorithme TITANIC prend fin quand il n'y plus
de candidats a generer.
TITANIC utilise la même structure de donnees (cad un
trie) que les algorithmes CLOSE et A-CLOSE. Il necessite au pire des cas
|I| accès au contexte d'extraction (|I| etant la taille
maximale possible d'un candidat generateur minimal).
2.2.2 Les algorithmes de type
!!Diviser-et-générer!!
Dans cette section, nous allons nous interesser aux
algorithmes les plus connus operant selon la strategie "Diviser-et-generer"
[34]. Ces algorithmes ne font qu'enumerer les item-sets fermes frequents [51].
Cette strategie, "Diviser-et-generer", est consideree comme une solution au
principal handicap des algorithmes de type "Generer-et-tester", a savoir la
generation d'un grand nombre de candidats. Malgre l'existence de plusieurs
algorithmes
opérant selon cette stratégie tels que CLOSET+
[65] et FP-CLOSE [30], ces derniers ne sont que des améliorations ou des
variantes de l'algorithme CLOSET proposé par Pei et al. [51].
L'algorithme CLOSET utilise une structure de données
avancée, basée sur la notion de trie, appelée arbre
FP-Tree [34, 35]. La particularité de cette structure réside dans
le fait que plusieurs transactions partagent un même chemin, de
longueur n dans l'arbre FP-Tree, s'ils ont les n premiers
items en commun. L'algorithme CLOSET effectue le processus d'extraction des
itemsets fermés fréquents en deux étapes successives [9]
:
1. Construction de l'arbre FP-Tree : Les items des
transactions sont ordonnés par support décroissant après
avoir élagué les items infréquents. Ensuite, l'arbre
FP-Tree est construit comme suit. Premièrement, le nceud racine est
créé et est étiqueté par "root". Pour chaque
transaction du contexte, les items sont traités et une branche est
créée suivant le besoin. Dans chaque nceud de la structure
FP-Tree, il y a un compteur qui garde la trace du nombre de transactions
partageant ce nceud. Dans le cas oft une transaction présente un
préfixe commun avec une branche dans le FP-Tree, le compteur de chaque
nceud appartenant a ce préfixe est incrémenté et une
sous-branche va être créée contenant le reste des items de
la transaction.
2. Exploration de l'arbre FP-Tree : Au lieu d'une exploration
en largeur d'abord des itemsets fermés candidats, CLOSET effectue une
partition de l'espace de recherche pour effectuer ensuite une exploration en
profondeur d'abord. Ainsi, il commence par considérer les 1-itemsets
fréquents, triés par ordre croissant de leurs supports
respectifs, et examine seulement leurs sous-contextes conditionnels (ou FP-Tree
conditionnels) [9]. Un sous-contexte conditionnel ne contient que les items qui
co-occurrent avec le 1-itemset en question. Le FP-Tree conditionnel
associé est construit et le processus se poursuit d'une manière
recursive.
Pour faciliter le parcours d'un FP-Tree, une table d'entete
lui est associée. Cette table contient la liste des items contenus dans
ce FP-Tree, triés par ordre décroissant de leurs supports
respectifs. Pour chaque item, son support est stocké ainsi qu'un lien
vers le premier nceud qui le contient. Des liens inter-nceuds permettent de
lier tous les nceuds contenant un même item dans le FP-Tree [34, 35].
concatenation des 1-itemsets qui sont aussi frequents que
p (dans le sous-contexte conditionnel).
P2 : Il n'y a nul besoin de developper un sous-contexte
conditionnel d'un itemset p qui est inclus dans un itemset ferme
frequent dejà decouvert c, tel que
Supp(p)=Supp(c). Dans ce cas, p est dit couvert
par c.
Pour calculer les fermetures, CLOSET traite les items
frequents un par un en commencant par le moins frequent. Pour chaque item
i, il construit son FP-Tree conditionnel. Un FP-Tree conditionnel relatif
à un item i contient l'ensemble des transactions on se trouve
i. Dans ce FP-Tree, i est exclu ainsi que les items
dejà traites, puisque tous les itemsets fermes frequents contenant ces
items traites ont ete dejà determines. Le FP-Tree conditionnel ne
contient alors que les items non traites et dont le support est superieur ou
egal à minsup. Cette condition est imposee pour ne generer que des
itemsets fermes qui sont frequents. La fermeture de i est egale
à sa concatenation avec les items de même support (d'apres P1). Le
même traitement est realise pour tout itemset forme par la concatenation
de i avec un item, dont le support dans le FP-Tree conditionnel est
different de celui de i. Ainsi, d'une maniere recursive et en operant
en profondeur d'abord, CLOSET determine tous les itemsets fermes frequents.
Pour reduire le cont du processus d'extraction, CLOSET ne developpe le FP-Tree
conditionnel d'un itemset p qu'apres avoir verifie que p
n'est pas couvert par un itemset ferme frequent c dejà
decouvert (d'apres P2) car sinon la fermeture de p est dejà
extraite.
Il est important de noter que CLOSET est gourmand en espace
memoire [9]. En effet, les appels recursifs necessitent de maintenir un nombre
generalement eleve de FP-Trees en memoire centrale. De plus, CLOSET necessite
de maintenir en memoire centrale les itemsets fermes frequents dejà
trouves et ceci afin d'accelerer le test associe à la propriete P2. Les
auteurs de CLOSET [51] affirment que leur algorithme ne genere pas de candidats
contrairement aux algorithmes de la premiere strategie. Cependant, pour des
supports bas et dans le cas de contextes epars, chaque generateur frequent est
un ferme. Ainsi, les deux proprietes sur lesquelles se base CLOSET ne donnent
plus l'effet escompte. D'on, l'itemset ferme frequent, extrait à partir
du sous-contexte conditionnel d'un itemset X, est egal à
X et n'est couvert par aucun itemset ferme frequent dejà trouve. De
ce fait, CLOSET construit recursivement un FP-tree conditionnel pour tout
itemset frequent (qui est lui même son propre ferme). Ceci rend eleve le
nombre de FP-trees presents en même temps en memoire centrale.
En plus du cont non negligeable de l'etape du tri du contexte
d'extraction, la structure
FP-Tree proposee est malheureusement non adaptee pour un
processus de fouille interactif, dans lequel l'utilisateur peut etre amene a
varier la valeur du support [9]. Dans ce cas, la structure doit etre
entièrement reconstruite [9]. Les travaux presentes dans [8, 19]
permettent de pallier cette insuffisance.
Notons que, l'algorithme CLOSET necessite deux accès au
contexte d'extraction : un premier accès pour extraire la liste des
1-itemsets frequents et un deuxième pour construire l'arbre FP-Tree.
2.2.3 Les algorithmes hybrides
Dans cette section, nous allons nous interesser aux
algorithmes adoptant la strategie hybride. Ces algorithmes ne font qu'enumerer
les itemsets fermes frequents [69]. Cette strategie evite le goulot
d'etranglement de la première strategie, a savoir la generation d'un
nombre eleve de candidats, et ceci en ne generant qu'un seul candidat a la
fois. En plus, cette strategie explore l'espace de recherche en profondeur
d'abord tel que les algorithmes bases sur la strategie
"Diviser-et-générer". Cependant, les algorithmes hybrides ne
divisent pas le contexte d'extraction en sous-contextes, evitant ainsi une
saturation de la memoire.
Dans la litterature actuelle, nous trouvons essentiellement un
seul algorithme implementant cette strategie, a savoir l'algorithme CHARM [69].
Des ameliorations de cet algorithme, tels que LCM [60, 61, 62] et DCI-CLOSED
[43, 44], ont ete aussi proposees.
L'algorithme CHARM a ete propose par Zaki et al. [69]. Il a
plusieurs caracteristiques, qui le distinguent des algorithmes adoptant les
deux premières strategies. En effet, contrairement a ces algorithmes qui
n'exploitent que l'espace des itemsets (fermes), CHARM explore simultanement
l'espace des itemsets fermes ainsi que celui des transactions. Pour cela, il
utilise une structure d'arbre particulière appelee IT-Tree
(Itemset-Tidset Tree) introduite dans [69]. Dans cette structure, chaque nceud
est forme par un couple compose par un itemset ferme frequent candidat ainsi
que l'ensemble des transactions auxquelles il appartient (cad son extension ou
tidset [69]).
CHARM determine tous les itemsets fermes frequents en
parcourant l'arbre IT-Tree a partir de la racine de gauche a droite et en
profondeur d'abord, en considerant un par un les 1-itemsets frequents tries par
ordre lexicographique. Le parcours en profondeur d'abord rappelle la strategie
"Diviser-et-générer".
L'algorithme CHARM opere de la maniere suivante : pour chaque
deux candidats item-sets fermes frequents A et B avant les
mimes nceuds parents, CHARM teste s'ils sont ou non des fermes et ceci en
comparant leurs tidsets. Pour cela, il distingue quatre cas [69] :
1. Si ø(A) =
ø(B) alors ã(A) =
ã(B) = ã(AUB). Ainsi, ni
A, ni B ne sont des itemsets fermes frequents. Alors, CHARM
remplace toutes les occurrences de A dans l'arbre IT-Tree par
(A U B) et elimine B de l'arbre.
2. Si ø(A) C
ø(B) alors ã(A)
ã(B) et ã(A)=
ã(A U B). Alors, l'itemset A ne peut etre un
itemset ferme frequent. Dans ce cas, toutes les occurrences de A dans
l'arbre IT-Tree sont remplacees par (A UB). B n'est pas
supprime de l'arbre IT-Tree car il peut etre un generateur d'un autre itemset
ferme frequent.
3. Si ø(A) D
ø(B) alors ã(A)
ã(B) et ã(B)=
ã(A U B). Alors, l'itemset B ne
peut etre un
itemset ferme frequent. Dans un tel cas, B est elimine de l'arbre
IT-Tree et (A U B) est ajoute comme descendant de A.
Ce dernier n'est pas supprime de l'arbre IT-Tree puisqu'il peut etre un
generateur d'un autre itemset ferme frequent.
4. Si ø(A)
ø(B) alors ã(A)
ã(B) ã(A U B). Ici, l'algorithme
CHARM ajoute
(A U B) comme descendant de A si et seulement
si (A U B) est frequent ; sinon l'arbre IT-Tree reste inchange (cad
dans le cas oft (A U B) est un itemset infrequent).
Dans les quatre cas mentionnes ci-dessus, la comparaison entre
ø(A) et ø(B) se fait en
effectuant l'intersection de ø(A) et
ø(B). La generation de (A U B) a partir de
A et B nous rappelle la phase combinatoire d'APRiORi-GEN [2].
Cependant, le resultat est toujours un candidat unique.
CHARM genere un candidat et calcule son support dans la
même etape. Si un candidat A ne peut plus etre etendu, CHARM ne
l'ajoute dans la liste des itemsets fermes frequents retenus que s'il n'est pas
couvert par un autre itemset ferme frequent appartenant a cette liste. Si
A est couvert alors il ne represente pas un itemset ferme. Notons que, ce
même test est effectue par CLOSET avant de developper un contexte
d'extraction conditionnel. Pour accelerer ce test de couverture, CHARM utilise
une table de hachage pour stocker les itemsets fermes frequents retenus [69].
Dans le cas oft A ne peut plus etre etendu, CHARM libere le lien qui
lie le nceud representant A et le nceud parent, car ce lien ne sert
plus a rien.
CHARM est ameliore par l'utilisation d'une representation de
donnees appelee Diffset [68] permettant un stockage incremental des
tidsets [9]. Dans cette structure, CHARM ne fait qu'enregistrer, pour chaque
candidat itemset ferme frequent, la difference qui existe
entre son intention et l'intention de son parent immediat.
Diffset permet d'accelerer le calcul des quatre cas mentionnes plus haut, etant
donne que l'intersection des transactions, resultat de la difference entre
ø(A) et ø(P) d'une part et
entre ø(B) et ø(P) d'autre
part (tel que P est le parent immediat de A et B),
est nettement plus rapide que l'intersection de ø(A)
et ø(B) [69]. Un autre avantage de Diffset est qu'il
permet aussi de reduire la memoire necessaire pour stocker les informations
relatives aux candidats contenus dans l'arbre IT-Tree [69] et ceci en reduisant
le stockage redondant des tidsets.
En revanche, l'inconvenient majeur de l'algorithme CHARM
reside dans le fait qu'il est exigeant en espace memoire. En effet, le fait de
stocker les itemsets et leurs tidsets ne fait qu'accroitre la quantite d'espace
memoire utilisee [9].
Enfin, signalons que l'algorithme CHARM necessite un seul
acces au contexte d'extraction pour determiner les listes des transactions
auxquelles appartiennent les items frequents du contexte en question.
2.3 Discussion
Il est bien connu que l'etape la plus complexe et la plus
consommatrice en temps d'execution est celle de la decouverte des itemsets
(fermes) frequents. Comme effet de bord, cette etape peut generer un nombre
important d'itemsets frequents et par consequent de regles d'association. Les
algorithmes bases sur l'extraction des itemsets fermes frequents sont une
nouvelle alternative avec la promesse claire de reduire considerablement la
taille de l'ensemble des regles d'association. Durant notre description des
principaux algorithmes d'extraction des itemsets fermes frequents, nous les
avons distingue par rapport A la strategie d'exploration adoptee. D'autres
criteres peuvent être utilises pour classer ces algorithmes tels que [43]
:
- Choix des generateurs : certains algorithmes ont choisi les
generateurs minimaux comme generateurs de chaque classe d'equivalence (cas de
l'algorithme CLOSE) tandis que d'autres optent pour une technique se basant sur
le fait qu'a chaque fois qu'un generateur est trouve, sa fermeture est
calculee. Ceci permettrait de creer de nouveaux generateurs a partir des
itemsets fermes frequents trouves (cas de l'algorithme CLOSET).
- Calcul de la fermeture : le calcul de la fermeture peut
être fait selon deux methodes. Dans la premiere methode, chaque fois
qu'un sous-ensemble de l'ensemble total des generateurs - caracterise par la
même taille des generateurs - est determine, la fermeture
de chaque generateur appartenant a ce sous-ensemble est
calculee (cas de l'algorithme CLOSE). Dans l'autre methode, le calcul des
fermetures de l'ensemble de tous les generateurs se fait dans une meme etape
(cas de l'algorithme A-CLOSE).
Le calcul de la fermeture d'un itemset X differe
aussi par le fait qu'il peut etre realise soit par des operations
d'intersection sur les transactions auxquelles appartient X (cad
son extension), soit d'une maniere incrementale en cherchant les items
appartenant a la fermeture d'un itemset X et qui verifient la relation
suivante : ø(X) C ø(i) =
i E ã(X), avec i un item
n'appartenant pas a X [55, 57].
Le probleme de decouverte des regles d'association, considere
sous l'optique de decouverte des itemsets fermes, pourrait etre reformule comme
suit [9] :
1. Decouvrir deux "systemes de fermeture" distincts, cad
ensembles d'ensembles fermes sous l'operateur d'intersection, a savoir
l'ensemble des itemsets fermes et l'ensemble des generateurs minimaux. Aussi,
la relation d'ordre sous-jacente devrait etre determinee.
2. A partir de toute l'information collectee, cad les deux
"systemes de fermeture" et la relation d'ordre sous-jacente, deriver des bases
generiques de regles d'association.
A la lumière de cette reformulation et en tenant compte
de l'objectif de reduire le nombre de regles d'association, nous considerons
les caracteristiques (ou dimensions) suivantes permettant de determiner les
buts realises (construction de la relation d'ordre, etc.) et de montrer les
differences majeures qui pourraient exister entre les algorithmes passes en
revue (strategie adoptee, elements generes, etc.). Ces caracteristiques sont
les suivantes
[9] :
1. Strategie d'exploration : trois strategies principales
sont utilisees afin d'explorer l'espace de recherche : "Generer-et-tester",
"Diviser-et-generer" et une strategie hybride qui beneficie des
avantages des deux premieres.
2. Espace de recherche : la valeur "exhaustive" de cette
dimension indique que toutes les transactions seront prises en compte lors du
premier balayage. En revanche, la valeur "echantillon" signifie que seul un
echantillon du contexte d'extraction sera considere du moins pour un premier
balayage [59].
3. Type du format des donnees : cette dimension peut prendre
comme valeur : format de donnees horizontal (etendu), format de donnees
vertical, relationnel, texte brut, donnees multimedia.
4. Structure de donnees : differentes structures de donnees
peuvent etre utilisees
pour stocker les informations nécessaires a
l'exécution d'un algorithme (pour stocker les candidats, le contexte
d'extraction, etc.). La structure la plus privilégiée semble etre
la structure trie.
5. Calcul des fermetures : nous distinguons principalement
deux faZons pour calculer la fermeture d'un générateur (minimal)
: soit via des intersections des transactions auxquelles il appartient (cad son
extension), soit d'une maniere incrémentale, cad via des recherches des
items susceptibles d'appartenir a la fermeture en question.
6. Elements generes en sortie : cette caractéristique
indique les éléments générés en sortie.
7. Ordre partiel : cette caractéristique indique si la
relation d'ordre sous-jacente des itemsets fermés fréquents a
été déterminée ou non.
Le tableau 2.1 résume les principales
caractéristiques des algorithmes de génération d'itemsets
fermés fréquents par rapport aux dimensions
présentées ci-dessus.
Une premiere constatation qui se dégage de ce tableau
est qu'aucun algorithme n'est arrivé a tenir la promesse avancée
par cette nouvelle alternative d'algorithmes en matiere de réduction de
la redondance des regles d'association. L'origine de cet échec
réside dans le fait qu'aucun de ces algorithmes n'a pu supporter le coUt
élevé de la construction de la relation d'ordre (cf. derniere
ligne du tableau 2.1). Cette derniere est une condition sine qua non pour
l'obtention de la base générique des regles d'association
approximatives [9].
Une deuxieme constatation concerne la notion de
générateur minimal. En effet, malgré l'importance de cette
derniere dans les bases génériques étant donné
qu'elle permet d'avoir des prémisses minimales, seuls les algorithmes
adoptant la stratégie "Générer-et-tester" permettent
l'extraction des générateurs minimaux (cf. avant derniere ligne
du tableau 2.1). Pour ces algorithmes, l'obtention des regles
génériques exactes peut se faire d'une maniere directe
étant donné qu'ils extraient les générateurs
minimaux fréquents. Pour pouvoir extraire les regles
génériques approximatives, ils nécessitent
l'exécution en aval d'un algorithme permettant de construire la relation
d'ordre partiel, tel que celui proposé par Valtchev et al. [64]. Les
algorithmes adoptant les deux autres stratégies se sont focalisés
sur l'énumération des itemsets fermés fréquents.
Pour obtenir les bases génériques de regles, ces algorithmes
nécessitent alors l'application de deux autres algorithmes. Le premier
permettra de construire l'ordre partiel et le second aura pour objectif de
retrouver les générateurs minimaux fréquents tel que JEN
[23]. Ce dernier permet de retrouver les générateurs minimaux a
condition que l'ordre partiel soit déjà construit.
|
CLOSE
|
A-CLOSE
|
TITANIC
|
CLOSET
|
CHARM
|
|
Stratégie d'ex-
ploration
|
Générer-et- tester
|
Générer-et- tester
|
Générer-et- tester
|
Diviser-et- générer
|
Hybride
|
|
Espace de re-
cherche
|
Exhaustive
|
Exhaustive
|
Exhaustive
|
Exhaustive
|
Exhaustive
|
|
Type du format des données
|
Format ho- rizontal
|
Format ho- rizontal
|
Format ho- rizontal
|
Format ho- rizontal
|
Format ho-rizontal ou vertical
|
|
Structure de
données
|
Trie
|
Trie
|
Trie
|
Trie
|
Trie
|
|
Calcul des fer- metures
|
Calcul d'intersec- tions des
extensions
|
Calcul d'intersec- tions des
extensions
|
Calcul incrémental
|
Calcul incrémental
|
Calcul incrémental
|
|
Eléments géné- rés en sortie
|
Générateurs minimaux
et itemsets
fermés fréquents
|
Générateurs minimaux
et itemsets
fermés fréquents
|
Générateurs minimaux
et itemsets
fermés fréquents
|
Itemsets fermés fréquents
|
Itemsets fermés fréquents
|
|
Ordre partiel
|
Non
|
Non
|
Non
|
Non
|
Non
|
TAB . 2.1: Caractéristiques des algorithmes CLOSE,
A-CLOSE, TITANIC, CLOSET et CHARM
Une troisième constatation concerne le colit induit par
le calcul de la fermeture. En effet, bien que ces algorithmes constituent une
alternative intéressante, dans le cas de contextes d'extraction denses,
leurs performances sont faibles dans le cas des contextes épars. En
effet, dans ce type de contexte, l'espace de recherche des itemsets
fermés fréquents tend a se confondre avec celui des itemsets
fréquents.
En comparant les algorithmes décrits dans ce chapitre,
nous pouvons noter aussi les remarques suivantes :
Parmi les cinq algorithmes, seul TITANIC considère la
classe d'équivalence dont l'en-
semble vide est le
générateur minimal. Ainsi, il est le seul algorithme dont les
éléments
générés permettent de construire
un treillis d'Iceberg en utilisant par exemple l'algo-
rithme proposé par Valtchev et al. [64].
CLOSE, A-CLOSE et TITANIC ont pour désavantage de
calculer la même fermeture plusieurs fois dans le cas oft elle admet
plusieurs générateurs minimaux. Cette lacune est
évitée par CLOSET et CHARM grace aux tests de couverture.
Cependant, afin d'accélérer ces tests, CLOSET et CHARM sont
obligés de maintenir en mémoire centrale, l'ensemble des itemsets
fermés fréquents trouvés. Le travail
présenté dans [43] essaie d'extraire les itemsets fermés
fréquents sans duplication et sans les maintenir en mémoire
centrale. Pour cela, les auteurs introduisent une stratégie permettant
la détection des duplications dans le calcul des fermetures.
Les stratégies d'élagage adoptées par
TITANIC sont une amélioration de celle de A-CLOSE. En effet, en
utilisant le support estimé d'un candidat, TITANIC évite le coUt
des balayages effectués par A-CLOSE pour comparer le support d'un
candidat générateur minimal de taille k aux supports de
ses sous-ensembles de taille (k-1). Les stratégies
d'élagage adoptées par CLOSET et celles utilisées dans
CHARM peuvent aussi être considérées comme les
mêmes.
2.4 Conclusion
Dans ce chapitre, nous avons présenté un
état de l'art sur les algorithmes d'extraction des itemsets
fermés (fréquents). Le constat majeur est que ces algorithmes se
sont focalisés sur l'extraction des itemsets fermés
fréquents en négligeant la composante relation d'ordre partiel
sous-jacente. Cette relation d'ordre partiel est primordiale pour la
génération de regles génériques approximatives. De
même, seuls les algorithmes adoptant la stratégie
"Générer-et-tester" permettent l'extraction des
générateurs minimaux. Ces derniers sont indispensables pour
l'obtention de regles d'association informatives (cad a prémisse
minimale et a conclusion maximale).
Dans le chapitre suivant, nous allons présenter un
nouvel algorithme, appelé PRINCE, permettant l'extraction de bases
génériques de regles d'association. Pour atteindre cet objectif,
l'algorithme PRINCE [33, 32] extrait les itemsets fermés
fréquents, leurs générateurs minimaux associés
ainsi que la relation d'ordre partiel tout en réduisant le coUt du
calcul des fermetures.
Chapitre 3
L'algorithme PRINCE
3.1 Introduction
L'utilisation des regles d'association est un domaine en
pleine expansion. En effet, de nos jours, l'exploitation des regles
d'association dépasse le cadre du panier de la ménagere,
introduit par Agrawal et al. en 1993 [1], pour s'intéresser a plusieurs
autres domaines tels que l'aide a planification commerciale [42], l'aide a la
recherche médicale [20], l'analyse des images, de données
spatiales, géographiques, etc [54]. Cependant, l'extraction des regles
d'association a partir des itemsets fréquents génere un nombre
généralement tres élevé de regles même pour
des contextes de tailles raisonnables (quelques milliers d'objets) [67]. Ainsi,
l'exploitation et la visualisation de ces regles devient de loin une
tâche facile pour l'utilisateur. Pour pallier cet inconvénient,
l'approche basée sur l'extraction des itemsets fermés
fréquents propose d'extraire, sans perte d'information, un sous-ensemble
de regles, a partir duquel nous pouvons retrouver toutes les autres regles
(redondantes) [5, 56, 67]. Ainsi, les bases génériques formant
les regles d'association informatives [4, 5] ont été introduites
pour obtenir des ensembles de regles informatives et pour présenter a
l'utilisateur les regles les plus pertinentes sans perte d'information. Un
survol critique des algorithmes, basés sur l'extraction des itemsets
fermés, montre que ces algorithmes ont failli a leurs objectifs [9]. En
effet, l'obtention des bases génériques de regles
nécessite l'extraction de trois composantes, a savoir les itemsets
fermés fréquents, leurs générateurs minimaux
associés ainsi que la relation d'ordre partiel sous-jacente. Cette
relation d'ordre partiel est une condition sine qua non pour l'obtention des
regles d'association génériques approximatives [9]. Les
générateurs minimaux permettent d'obtenir les regles les plus
informatives pour l'utilisateur. Les notions d'ordre partiel et de
générateur mi-
nimal sont donc primordiales. Cependant, la quasi-totalite des
algorithmes reposant sur cette approche, cad celle de l'extraction des itemsets
fermes frequents, se sont focalises sur l'extraction de la premiere composante,
cad les itemsets fermes frequents, en negligeant les deux dernieres
composantes. Seuls les algorithmes adoptant la strategie "Generer-ettester"
font mieux en permettant aussi l'extraction des generateurs minimaux, sans se
soucier de la construction de la relation d'ordre partiel.
Dans ce chapitre, nous allons introduire un nouvel algorithme,
appele PRINCE, pour l'extraction des itemsets fermes frequents, leurs
generateurs minimaux respectifs ainsi que la determination de la relation
d'ordre partiel. A cet effet, PRINCE construit une structure partiellement
ordonnee appelee treillis des generateurs minimaux [7]. La principale
originalite de l'algorithme PRINCE reside dans le fait que cette relation
d'ordre est maintenue entre les generateurs minimaux et non plus entre les
itemsets fermes. Ainsi, les bases generiques de regles sont obtenues par un
simple balayage de la structure partiellement ordonnee sans avoir a calculer
les fermetures.
Dans ce chapitre, nous commencons par decrire les etapes
constituant l'algorithme PRINCE ainsi que la structure de donnees qu'il
utilise. Ensuite, nous montrons sa validite, sa terminaison ainsi que sa
completude. Enfin, nous cloturons la presentation de notre algorithme par une
etude de sa complexite theorique.
3.2 L 'algorithme PRINCE
Dans cette section, nous allons introduire un nouvel
algorithme, appele PRINCE, dont l'objectif principal est de pallier la
principale lacune des algorithmes dedies a l'extraction des itemsets fermes
frequents, cad ne pas construire la relation d'ordre partiel. La principale
originalite de PRINCE est qu'il construit une structure partiellement ordonnee
appelee treillis des generateurs minimaux [7]. Dans cette structure, l'ordre
partiel est maintenu non plus entre les itemsets fermes frequents mais entre
leurs generateurs minimaux associes. De plus, PRINCE met en place un mecanisme
de gestion des classes d'equivalence permettant de generer la liste integrale
des itemsets fermes frequents sans duplication et sans recours aux tests de
couvertures. Il permet aussi de reduire d'une maniere notable le cofit du
calcul des fermetures et ceci en utilisant les notions de blo queur minimal et
de face introduites par Pfaltz et Taylor dans [52].
support minsup et le seuil minimal de confiance minconf. Il
donne en sortie : la liste des itemsets fermes frequents, leurs generateurs
minimaux associes ainsi que les bases generiques de regles. PRINCE opere en
trois etapes successives :
1. Determination des generateurs minimaux ;
2. Construction du treillis des generateurs minimaux ;
3. Extraction des bases generiques informatives de regles. 3.2.1
Determination des generateurs minimaux
Avant de commencer la description de cette premiere etape, nous
allons commencer par introduire la definition d'un treillis des generateurs
minimaux :
Definition 6 [7] Un treillis des generateurs minimaux est une
structure equivalente au treillis d'Iceberg tel que dans cha que
classe d'equivalence, nous ne trouvons que les generateurs minimaux frequents
correspondants.
En adoptant la strategie "Generer-et-tester", l'algorithme
PRINCE parcourt l'espace de recherche par niveau pour determiner l'ensemble des
generateurs minimaux frequents, note gMFK, ainsi que la bordure
negative des generateurs minimaux, notee gBd-.
PRINCE utilise, dans cette etape, les memes strategies d'elagage que TITANIC,
cad minsup, l'ideal d'ordre regissant des generateurs minimaux frequents et le
support estime.
Le pseudo-code relatif a cette etape est donne par la procedure
GEN-GMs (cf. Algorithme 1). Les notations utilisees sont resumees dans le
tableau 3.1.
La procedure GEN-GMs prend en entree le contexte
d'extraction 1C et le support minimal minsup. Elle donne en sortie
l'ensemble des generateurs minimaux frequents gMFK de faZon a pouvoir
les parcourir par ordre decroissant de leurs supports respectifs lors de la
deuxieme etape de l'algorithme PRINCE. gMFK est alors
considere comme etant divise en plusieurs sous-ensembles. Chaque sous-ensemble
est caracterise par la meme valeur du support. Ainsi, chaque fois qu'un
generateur minimal frequent est determine, il est ajoute a l'ensemble
representant son support. La procedure GEN-GMs garde aussi la trace des
generateurs minimaux infrequents, formant la bordure negative
gBd-, afin de les utiliser lors de la deuxieme
etape.
k : un compteur qui indique l'iteration courante. Durant
la ki`eme iteration, tous les k-generateurs minimaux
sont determines.
GMCk : ensemble des k-generateurs minimaux
candidats.
GMFk : ensemble des k-generateurs minimaux
frequents.
GMFK : ensemble des generateurs minimaux frequents tries
par ordre decroissant du support.
GBd- : bordure negative des generateurs
minimaux.
Chaque element c de GMCk ou de GMFk
est caracterise par les champs suivants :
1. support-reel : support reel de c.
2. sous-ens-directs : liste des sous-ensembles de c de
taille (k-1).
Chaque element c de GMCk est aussi
caracterise par un support estime (le champ support-estime ) et qui sera
utilise pour eliminer les candidats non generateurs minimaux.
TAB . 3.1 -- Notations utilisees dans la procedure GEN-GMs

3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
1 Procedure : GEN-GMs
Donnees : - K : contexte d'extraction, minsup.
Resultats :
1. GMFK : ensemble des générateurs
minimaux fréquents.
2. GBd- : bordure négative
des générateurs minimaux. 2 debut
GMC1 = I ;
CALCUL-SUPPORT (GMC1);
Ø.support-réel =1O1; GMF0 =
{Ø}; pour chaque (c ? GMC1) faire si
(c.support-réel = 1O1) alors
ã(Ø)=ã(Ø) ?
c;
sinon
si (c.support-réel = minsup) alors
c.sous-ens-directs ={Ø};
GMF1=GMF1 ? c;
sinon
pour (k=1; GMFk =~ Ø ;
k++) faire

GMF(k+1)=GEN-GMs-sUIVANT(GMFk);
retourner GMFK=?:GMFi C i =
0..k}
19 fin
Algorithme 1 : GEN-GMs

3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
21
22
23
1 Procedure : GEN-GMS-SUIVANT Donnees : - GMFk.
Resultats : - GMF(k+1).
2 debut
/* Phase 1 : APRIORI-GEN. */
GMC(k+1)=APRIORI-GEN(GMFk)
/* Phase 2 : Vérification de l'idéal d'ordre
régissant les générateurs minimaux fréquents. */
pour chaque (c ? GMC(k+1)) faire
c.support-estimé = 1O1; /* support maximal possible */
pour chaque (c1 tel que |c1|
= k et c1 ? c) faire si (c1
?/ GMFk) alors
GMC(k+1) = GMC(k+1) --
c;
arrêt;
fin pour;
c.support-estimé =
min(c.support-estimé,
c1.support-réel ); c.sous-ens-directs =
c.sous-ens-directs ? c1;
/* Phase 3 : Calcul des supports des candidats et élagage.
*/
CALCUL-SUPPORT (GMC(k+1)); pour
chaque (c ? GMC(k+1)) faire si
(c.support-réel c.support-estimé et
c.support-réel = minsup) alors
GMF(k+1)=GMF(k+1) ?
c;
sinon
20

si (c.support-réel < minsup) alors
GBd- = GBd- ? c;
retourner GMF(k+1)
24 fin
Algorithme 2 : GEN-GMS-SUIVANT
(ligne 3). Le support des items est alors calculé via
un accès au contexte d'extraction (ligne 4). Le support de l'ensemble
vide est égal au nombre de transactions du contexte d'extraction, cad
1O1 (ligne 5). L'ensemble vide, étant le
générateur minimal fréquent de taille 0, est
inséré dans gmF0 (ligne 6). Pour tout 1-itemset
c, nous distinguons les trois cas suivants (lignes 7-15) :
1. Si c a le même support que celui de l'ensemble
vide, alors c appartient a la fermeture de l'ensemble vide. Le
1-itemset c n'est donc pas un générateur minimal.
2. Si c a un support supérieur ou égal
a minsup, alors c est un générateur minimal
fréquent et est ajouté a gmF1. Le seul sous-ensemble
direct de c étant l'ensemble vide.
3. Si c est infréquent alors c est
ajouté à la bordure négative gBd- (1).
Ensuite, le parcours se fait par niveau. Pour cela, nous
utilisons la procédure GEN-GMSSUIVANT (lignes 16-17) dont le pseudo-code
est donné par l'algorithme 2. La procédure GEN-GMS-SUIVANT prend
en entrée l'ensemble des générateurs minimaux
fréquents de taille k et retourne l'ensemble des
générateurs minimaux fréquents de taille (k+1).
La première étape de l'algorithme PRINCE prend fin lorsqu'il n'y
a plus de candidats a générer. Elle retourne alors l'ensemble des
générateurs minimaux fréquents gmFK trié
par ordre décroissant des supports (ligne 18).
La première phase de la procédure
GEN-GMS-SUIVANT consiste a effectuer la jointure des générateurs
minimaux fréquents d'une itération k pour obtenir
l'ensemble des candidats (k+1)-générateurs minimaux,
cad gmC(k+1) (lignes 3-4). Lors de la deuxième phase
et pour chaque candidat c E gmC(k+1), nous testons s'il
vérifie l'idéal d'ordre des générateurs minimaux
fréquents (lignes 5-14). En même temps, nous calculons le support
estimé de c et qui est égal au minimum des supports de
ses sous-ensembles de taille k (ligne 13). Des liens vers ces derniers
sont stockés dans le champ sous-ens-directs et qui seront
utilisés dans la seconde étape de l'algorithme PRINCE (ligne 14).
Si c ne vérifie pas l'idéal d'ordre alors c est
éliminé de gmC(k+1) (lignes 9-12). Une fois le
test de l'idéal d'ordre effectué, nous entamons la
troisième phase (lignes 15-22). Ainsi, un accès au contexte
d'extraction permettra de calculer les supports réels des candidats
retenus dans gmC(k+1) (ligne 16). Une fois cet accès
effectué, le support réel de chaque candidat c de
gmC(k+1), est comparé a son support estimé
(lignes 17-22). Si ces derniers sont égaux, c
n'est pas un generateur minimal. Sinon, c est un
generateur minimal et la comparaison de son support reel avec minsup permettra
de le classer parmi les generateurs minimaux frequents ou parmi ceux
infrequents (lignes 18-22). Apres l'execution de ces trois phases, la procedure
GEN-GMS-SUIVANT retourne l'ensemble des generateurs minimaux frequents de
taille (k+1) (ligne 23).
Dans la suite, nous allons noter par support, au lieu de
support-reel, le champ contenant le support reel de chaque generateur minimal
etant donne que nous n'avons plus a distinguer entre le support reel et le
support estime d'un itemset.
3.2.2 Construction du treillis des generateurs minimaux
L'objectif de cette etape est d'organiser les generateurs
minimaux frequents sous forme d'un treillis des generateurs minimaux et sans
effectuer un acces supplementaire au contexte d'extraction. Pour
atteindre cet objectif, les listes des successeurs immediats(2)
seront modifiees d'une maniere iterative. Ainsi, nous parcourons l'ensemble
trie GMFK en introduisant un par un les generateurs minimaux frequents
dans le treillis des generateurs minimaux.
Chaque generateur minimal frequent g de taille
k (k = 1) est introduit dans le treillis des generateurs
minimaux en le comparant avec les successeurs immediats de ses sous-ensembles
de taille (k-1). Rappelons que des liens vers ces derniers ont ete
stockes dans le champ sous-ens-directs des la premiere etape. Ceci est base sur
la propriete d'isotonie de l'operateur de fermeture [21]. En effet,
si g1 est inclus dans g tel que
Ig1l--(k-1) alors la fermeture de
g1, ã(g1), est incluse dans
la fermeture de g, ã(g). Ainsi, la classe
d'equivalence a laquelle appartient g est un successeur -- pas
forcement immediat -- de la classe d'equivalence a laquelle appartient
g1.
En comparant g a la liste des successeurs immediats
de g1, disons L, deux cas sont a distinguer.
Si L est vide alors g est simplement ajoute a L.
Sinon, g est compare aux elements appartenant a L (cf.
Proposition 3 ci-dessous). Pour chaque comparaison, les deux cas presentes dans
la proposition 3 sont alors a distinguer en remplacant X par
g et Y par un des elements de L.
emme 1 [55, 571 Soient X, Y ? I, X ? Y
? Supp(X) = Supp(Y ) ã(X)
= ã(Y ).
Proposition 3 [32] Soient X, Y ? GMFK,
CX et CY dénotent leurs classes d'équivalence
respectives :
a. Si Supp(X) = Supp(Y ) = Supp(X ? Y
) alors X et Y appartiennent a la meme classe
d'équivalence.
b. Si Supp(X) < Supp(Y ) et
Supp(X) = Supp(X ? Y ) alors CX (resp. CY )
est un successeur (resp. prédécesseur) de CY
(resp. CX).
Preuve.
a.
(1) X ? (X ? Y ) ?
Supp(X)=Supp(X ? Y ) ã(X) =
ã(X ? Y ) (d'apres Lemme 1)
(2) Y ? (X ? Y ) ? Supp(Y
)=Supp(X ? Y ) ã(Y ) =
ã(X ? Y ) (d'apres Lemme 1) D'apres (1) et (2),
ã(X)=ã(Y ) et donc X
et Y appartiennent a la même classe d'équivalence
(cad CX et CY sont identiques).
b.
(1) X ? (X ? Y ) ?
Supp(X)=Supp(X ? Y ) ã(X) =
ã(X ? Y ) (d'apres Lemme 1)
(2) Y ? (X ? Y ) ? Supp(Y )
Supp(X ? Y ) ã(Y )? ã(X
? Y ) or d'apres (1),
ã(X) =
ã(X ? Y ) et donc ã(Y ) ?
ã(X) d'oft CX (resp. CY ) est un
successeur (resp. prédécesseur) de CY
(resp. CX).

Le calcul du support de (X ? Y ) se fait d'une
maniere directe si (X ? Y ) est un générateur minimal.
Dans ce cas, CX et CY sont incomparables. Sinon, la
proposition 2 (cf. page 29) est appliquée. La recherche du support
s'arrete des qu'un générateur minimal inclus dans (X ? Y
) et ayant un support inférieur strictement a celui de X
et a celui de Y est trouvé. Dans ce cas, CX et
CY sont incomparables.
Lors de ces comparaisons et pour éviter une des lacunes
des algorithmes adoptant la stratégie "Générer-et-tester",
a savoir le calcul redondant des fermetures, PRINCE utilise deux fonctions qui
se completent. Ces fonctions permettent de maintenir la notion de classe
d'équivalence tout au long du traitement. A cet effet, chaque classe
d'équivalence C sera caractérisée par un
représentant, qui est le premier générateur minimal
fréquent introduit dans le treillis des générateurs
minimaux. Tout générateur minimal fréquent g est
initialement considéré comme représentant de
Cg et le restera tant qu'il n'est pas comparé a un
générateur minimal fréquent précédemment
introduit dans le treillis des générateurs minimaux et
appartenant a Cg. Les deux fonctions sont décrites
dans ce qui suit [33, 32] :
1. La fonction GESTION-CLASSE-EQUIV : lors de la comparaison
d'un generateur minimal frequent, disons g, avec les elements d'une
liste L de successeurs immediats d'un autre generateur minimal
frequent, la fonction GESTION-CLASSE-EQUIV est invoquee dans le cas oft
g est compare au representant de sa classe d'equivalence, disons
R. La fonction GESTION-CLASSE-EQUIV remplace alors toutes les occurrences
de g par R dans les listes des successeurs immediats oft
g a ete ajoute. Les comparaisons de g avec le reste des elements
de L s'arretent car elles ont ete effectuees avec R. Ensuite,
le reste des comparaisons a effectuer par g sera fait via le
representant R. Ainsi, pour chaque classe d'equivalence, seul son
representant figure dans les listes des successeurs immediats. Cette fonction
permet d'optimiser la gestion des classes d'equivalence en minimisant les
comparaisons inutiles.
2. La fonction REPRESENTANT : cette fonction permet de
retrouver, pour chaque generateur minimal frequent g, le
representant R de sa classe d'equivalence afin de completer la liste
des successeurs immediats de Cg et qui est stocke au niveau
du representant R. Ceci permet de n'avoir a gerer qu'une seule liste
de successeurs immediats pour tous les generateurs minimaux frequents
appartenant a une meme classe d'equivalence.
Le pseudo-code de la deuxieme etape est donne par la procedure
GEN-ORDRE (cf. Algorithme 3). L'ensemble trie GMFK contient les
generateurs minimaux frequents ex-traits a partir du contexte d'extraction
K. En plus des champs utilises dans la premiere etape (cf. Tableau 3.1
page 42), a chaque element g de GMFK est associe le champ
succs-immediats pour contenir la liste des successeurs immediats de g.
A la fin de l'execution de la procedure GEN-ORDRE, cette liste est vide si
g n'est pas le representant de sa classe d'equivalence ou si g
appartient a une classe d'equivalence n'ayant pas de successeurs. Sinon, cette
liste ne contiendra que des representants.
La procedure GEN-ORDRE introduit un generateur minimal
frequent g dans le treillis des generateurs minimaux en le comparant
aux listes des successeurs immediats de ses sous-ensembles de taille
(k-1) (ligne 3). Soit g1 un des sous-ensembles
de g (ligne 4). La procedure GEN-ORDRE retrouve le representant de la
classe d'equivalence de g1 moyennant l'utilisation de la
fonction REPRESENTANT (ligne 5). Soit L la liste des successeurs
immediats de Cg1 stockee au niveau de son representant
R. L est donc egale a R.succs-immediats . L'ordre
decroissant par rapport aux supports, impose dans l'ensemble GMFK,
permet de ne distinguer que deux cas dans chaque comparaison de g avec
un element de L. En effet, si nous appelons g2 un
des elements de L, alors si la classe
d'equivalence de g et celle de g2
sont comparables, g et g2 doivent verifier une des
deux conditions presentees dans la proposition 3 (avec
X=g, Y=g2 et
Supp(g)=Supp(g2)). Si aucune de ces deux
conditions n'est verifiee, g et g2 appartiennent a
des classes d'equivalence incomparables. Si g et
g2 verifient la premiere condition de la proposition 3, alors
g et g2 appartiennent a la meme classe
d'equivalence (g2 est le representant de
Cg) et les traitements relatifs a la gestion de la classe
d'equivalence Cg sont realises moyennant un appel a la
fonction GESTTON-CLASSE-EQUT (lignes 7-8). Si g et
g2 verifient la deuxieme condition de la proposition 3,
alors Cg est un successeur de
Cg2 et nous comparons d'une maniere recursive
g a la liste des successeurs immediats de g2 (lignes
10-11). Pour le reste des elements de L, disons
L1, nous ne comparons g qu'aux elements ayant un
support strictement superieur a celui de g (ligne 12). En effet,
g n'appartient a aucune des classes d'equivalence representees par les
elements de L1 car sinon il ne serait pas un successeur
de g2. Si nous appelons g3 un des
elements de L1, et si Cg et
Cg3 sont comparables, Cg ne peut etre qu'un
successeur de Cg3 et nous comparons la liste des
successeurs immediats de g3 a g. Si la classe
d'equivalence de g est incomparable avec celles de tous les elements
de L, alors g est ajoute a L (ligne 13-14). Il faut
noter que ces comparaisons sont de nombre fini etant donne que le nombre
d'elements de chaque liste de successeurs immediats est fini et il en est de
meme pour le nombre de generateurs minimaux frequents dejà introduits
dans le treillis des generateurs minimaux.
Remarque 1
· Notons que si nous avons opte
pour n'importe quel autre ordre dans le tri de GMFK (par
exemple, tri par ordre croissant par rapport aux supports) et si g
est incomparable avec tous les elements de L, les
comparaisons de g avec les listes des successeurs immediats des
representants formant L seraient dans ce cas obligatoires. En
effet, deux classes d'equivalence incomparables (celle de g
et celle d'un representant appartenant à L) peuvent avoir des
successeurs en commun existants dejà dans le treillis des
generateurs minimaux. Ainsi, n'importe quel autre choix de tri
augmenterait considerablement le nombre, et par consequent le coat, des
comparaisons pour construire le treillis des generateurs minimaux.
· L'utilisation de la bordure negative des
generateurs minimaux GBd- dans le mecanisme de comptage par
inference [6J est une consequence du fait que son union avec l'ensemble des
generateurs minimaux frequents GMFK forme une representation
concise de l'ensemble des itemsets frequents [39, 40J. Ainsi, en
utilisant l'ensemble resultat de cette union, nous pouvons retrouver
le support de tout itemset sans effectuer un accès au contexte
d'extraction [39, 40J.

3
4
5
6
7
8
9
10
11
12
13
14
1 Procedure : GEN-ORDRE
Donnees : - GMFK.
Resultats : - Les elements de GMFK ordonnes
partiellement sous forme d'un treillis des générateurs
minimaux.
2 debut
pour chaque (g ? GMFK) faire pour chaque
(g1 ? g.sous-ens-directs) faire R =
REPRESENTANT (g1); pour chaque
(g2 ? R.succs-immédiats ) faire si
(g.support = g2.support = Supp(g ?
g2)) alors GESTION-CLASSE-EQUIV
(g,g2); /*g,g2 ?
Cg et g2 est le representant de
Cg*/
sinon
si (g.support < g2.support
et g.support = Supp(g ?g2)) alors g est
compare a g2.succs-immédiats ; /* Pour le
reste des elements de R.succs-immédiats , g n'est
compare qu'avec tout g3 tel que
g3.support > g.support ; */

si (? g2 ?
R.succs-immédiats, Cg et
Cg2 sont incomparables) alors
R.succs-immédiats = R.succs-immédiats ?
{g};
15 fin
Algorithme 3 : GEN-ORDRE
3.2.3 Extraction des bases generiques informatives de
regles
Dans cette etape, PRINCE extrait les regles generiques
informatives valides formees par l'union de la base generique de regles exactes
et de la reduction transitive de la base informative de regles approximatives.
Ainsi, pour chaque classe d'equivalence, PRINCE retrouve l'itemset ferme
frequent correspondant via l'application de la proposition 4 don-nee
ci-dessous. La preuve de la proposition 4 necessite d'introduire les
definitions et le theoreme suivants :
est dit minimal s'il n'existe aucun blo queur
B1 de G inclus dans B.
Definition 8 Soient f, f1 ?
IFFK. Si f couvre f1 dans le treillis
d'Iceberg ( àL, ? ) alors la face
de f par rapport a f1, notée
face~f&f1~, est égale a :
face(fIf1) = f - f1.
Theoreme 2 Soient f ? IFFK et GMf l'ensemble
de ses générateurs minimaux. Si f1 ?
IFFK tel que f couvre f1 dans le treillis
d'Iceberg ( àL,? ) alors
face(fIf1) est un blo queur minimal
de GMf [527.
Proposition 4 Soient f et f1
? IFFK tels que f couvre f1 dans le treillis
d'Iceberg ( àL,? ). Soit GMf
l'ensemble des générateurs minimaux de f. Alors,
l'itemset fermé fréquent f est égal a
: f = ?{g|g ? GMf} ? f1.
Preuve.Etant donne que l'union des elements de GMf
est un bloqueur de GMf, la face(fIf1),
qui est un bloqueur minimal pour GMf d'apres le Theoreme 2, est
incluse dans l'union des elements de GMf. Ainsi, il suffit de calculer
l'union de f1 avec les elements de GMf pour
retrouver f.

Il est a noter que Proposition 4 a pour avantage d'assurer
l'extraction sans redondance de l'ensemble des itemsets fermes
frequents. Le pseudo-code de cette etape est donne par la procedure GEN-BGRs
(cf. Algorithme 4) (3). Nous utilisons les mêmes notations que
celles des algorithmes precedents, auxquelles nous ajoutons le champ iff
pour chaque element de GMFK. Ainsi pour chaque generateur minimal
frequent g, ce champ permet de stocker l'itemset ferme frequent
correspondant a Cg si g est son representant. Dans
la procedure GEN-BGRs, L1 designe la liste des classes
d'equivalence a partir desquelles sont extraites les regles d'association
informatives. Par L2, nous designons la liste des classes
d'equivalence qui couvrent celles formant L1.
L'ensemble des regles informatives exactes BG est
initialement vide (ligne 3). Il en est de même pour l'ensemble des regles
informatives approximatives RI (ligne 4). Le parcours du treillis des
générateurs minimaux s'effectue d'une maniere ascendante en
partant de la classe d'equivalence dont le generateur est l'ensemble vide
(notee CØ). Ainsi, L1 est initialisee a
l'ensemble vide (ligne 5). Rappelons que la fermeture de l'ensemble vide a
dejà ete calculee des la premiere etape en collectant les items qui se
repetent dans toutes
3BGR est l'acronyme de Base Générique de
Regles.
les transactions (cf. ligne 8-9 de l'algorithme 1 page 43). La
liste L2 est initialement vide (ligne 6). Les traitements
de cette étape s'arrêtent lorsqu'il n'y a plus de classes
d'équivalence à partir desquelles seront extraites des regles
génériques (ligne 7). Si la fermeture de l'ensemble vide n'est
pas nulle, la regle exacte informative mettant en jeu l'ensemble vide et sa
fermeture sera extraite (ligne 9-10). Ayant l'ordre partiel construit, GEN-BGRs
extrait les regles approximatives informatives valides mettant en jeu
l'ensemble vide et les itemsets fermés fréquents de la couverture
supérieure de CØ (lignes 11-16). Ces fermetures sont
retrouvées en utilisant la proposition 4 en utilisant les
générateurs minimaux fréquents de chaque classe
d'équivalence et la fermeture de l'ensemble vide (ligne 11). Cette
couverture supérieure est stockée afin que le même
traitement soit réalisé pour les classes d'équivalence la
composant (ligne 12). Une fois les traitements relatifs à la classe
d'équivalence de l'ensemble vide terminés, L1
prendra pour valeur le contenu de L2 (ligne 17) afin de
ré-appliquer le même processus aux classes d'équivalence
qui sont des successeurs immédiats de CØ.
L2 est ré-initialisée au vide (ligne 18) et
contiendra les successeurs immédiats des classes d'équivalence
contenues dans L1. Etant donné qu'une classe
d'équivalence peut avoir plusieurs prédécesseurs
immédiats, un test est réalisé pour vérifier
qu'elle n'a pas déjà été insérée
dans L2. Ce test consiste à vérifier si
l'itemset fermé fréquent correspondant a déjà
été calculé (ligne 12). De la même maniere, GEN-BGRs
traite les niveaux supérieurs du treillis des générateurs
minimaux jusqu'à atteindre ses sommets (cad les classes
d'équivalence n'ayant pas de successeurs). L1 serait
alors vide et la condition de la ligne 7 ne sera plus vérifiée.
Ainsi, la troisieme étape de l'algorithme PRINCE prend fin et toutes les
regles génériques sont extraites.
Exemple 4 Afin d'illustrer le déroulement de
l'algorithme PRINCE, considérons le contexte d'extraction K
donné par la Figure 3.1 pour minsup = 2 et minconf = 0,5. La
première étape permet de déterminer l'ensemble
des générateurs minimaux GMFK trié, ainsi que
la bordure négative GBd-. GMFK
= {(Ø,5),(B,4),(C,4), (E,4), (A,3), (BC,3),(CE,3),
(AB,2), (AE,2)} et GBd-={ (D,1)}. Dans la
deuxième étape, PRINCE parcourt GMFK en comparant cha
que générateur minimal fréquent g de taille k
(k = 1) aux listes des successeurs immédiats de ses
sous-ensembles de taille (k-1). L'ensemble vide, n'ayant aucun
sous-ensemble, est introduit directement dans le treillis des
générateurs minimaux (cf. Figure 3.2.a). Ensuite, B est
ajouté a Ø.succs-immédiats (cf. Figure 3.2.b),
la liste des successeurs immédiats du Ø,
initialement vide. Ensuite, C sera comparé a B. BC étant
un générateur minimal, CB et CC sont alors
incomparables et C est ajouté a Ø.succs-immédiats
(cf. Figure 3.2.c). E est alors comparé a cette liste. En comparant E
1 Procedure : GEN-BGRs Donnees :
1. Le treillis des générateurs minimaux.
2. Le seuil minimum de confiance minconf. Resultats
:
1. L'itemset fermé fréquent de chaque classe
d'équivalence.
2. La base générique de regles exactes
BG.
3. La réduction transitive des regles approximatives
RI.
2 debut
|
3
4
5
6
7
|
BG=Ø;
RI=Ø;
L1={Ø};
L2=Ø;
tant que (L1 Ø) faire
|
|
8
|
|
pour chaque (g ? L1) faire
|
|
9
|
|
|
si (g.iff g) alors
|
|
10
|
|
|
|
BG = BG ? {(t (g.iff --
t), g.support ) | t ? GMFK et t ?
|
|
|
|
|
Cg} ;
|
|
11
|
|
|
pour chaque g1 ? g.succs-immediats
faire
|
|
12
|
|
|
|
si (g1.iff=Ø) alors
|
|
13
|
|
|
|
|
g1.iff=? {t ? GMFK t ?
Cg1 } ? g.iff;
|
|
14
|
|
|
|
|
L2=L2 ? {g1};
|
|
15
|
|
|
|
si ((g1.support/g.support )
= minconf) alors
|
|
16
|
|
|
|
|
RI = RI ? {(t
(g1.iff -- t), g1.support
, g1.support /g.support ) | t ? GMFK
et t ? Cg};
|
|
17
|
|
L1= L2;
|
|
18
|
|
L2= Ø;
|
19 fin
a B, E.support = B.support = Supp(BE) et donc E ? CB
dont B est le représentant (cf. Figure 3.2.d). La fonction
GESTION-CLASSE-EQUIV est alors appli quée et ceci en remplaçant
les occurrences de E par B dans des listes des successeurs immédiats
(dans ce cas, il n'y a aucune occurrence) et en poursuivant les
comparaisons avec B au lieu de E (dans ce cas, il n'y a plus de
comparaisons a faire via E). Les traitements s'arrétent alors pour
E. A ce moment du traitement, Ø.succs-immédiats =
{B,C}. Le générateur minimal fréquent A est alors
comparé a B. Comme AB ? GMFK, CB et CA sont
incomparables. Par contre, en comparant A et C, A.support <
C.support et A.support = Supp(AC) et donc CA est un
successeur de CC. Le générateur minimal A est tout
simplement ajouté a C.succs-immédiats étant
donné qu'elle est encore vide (cf. Figure 3.2.e). BC est
comparé aux listes des successeurs immédiats de B et de
C. La liste des successeurs immédiats de B est vide, BC est
alors ajouté. La liste des successeurs immédiats de C contient A.
Le générateur minimal fréquent BC est alors comparé
a A et comme BC.support = A.support mais BC.support =~
Supp(ABC), CBC et CA sont incomparables et BC est donc
ajouté a C.succs-immédiats (cf. Figure 3.2.f ). CE est
comparé aux listes des successeurs immédiats de C et de E. Celle
de C contient A et BC. CCE et CA sont incomparables, puis
que CE.support = A.support mais CE.support =~ Supp(ACE). En
comparant CE a BC, CE.support = BC.support = Supp(BCE) alors l'itemset
CE va étre affecté a la classe d'équivalence de
BC et les fonctions de gestion des classes d'équivalence sont invo
quées (cf. Figure 3.2.g). En particulier, les comparaisons de
CE aux successeurs immédiats de CE seront faites avec BC.
Comme CE a pour représentant B, BC est donc comparé aux
éléments de B.succs-immédiats. Cependant, comme
B.succs-immédiats ne contient que BC alors les comparaisons se
terminent. Le méme traitement est appli qué pour AB et
AE. Ainsi, la procédure de construction de l'ordre partiel prend
fin. Le treillis des générateurs minimaux obtenu est donné
par la figure 3.2.h. Pour la dérivation des règles
généri ques, le treillis des générateurs
minimaux est parcouru d'une manière ascendante a partir de
Co. Comme ã(Ø) = Ø, il n'y
a donc pas de règle exacte informative relative a
Co. Ø.succs-immédiats={B,C}. L'itemset fermé
fréquent correspondant a CB est alors retrouvé
et est égal a BE (cf. Figure 3.2.i). La règle informative
approximative valide Ø BE de support 4 et de confiance 0,8 sera
alors extraite. Il en est de méme pour la règle
Ø C, ayant les mémes valeurs de support et de confiance que
la précédente. De la méme manière et a
partir de CB et CC, le parcours du treillis se fait d'une
facon ascendante jus qu'a extraire toutes les règles
d'association informatives valides.
A la fin de l'exécution de l'algorithme, nous obtenons le
treillis d'Iceberg associé au
contexte d'extraction K (cf. Figure 3.2.i)(4)
ainsi que la liste les regles informatives valides, donn~e par la Figure
3.3.
3.3 Structure de donnees utilisee
Lors de la premiere etape, nous avons utilise un arbre prefixe
(ou trie) pour stocker les generateurs minimaux retenus. L'utilisation d'un
seul trie a ete motivee par le fait que l'ensemble des generateurs
minimaux GMK d'un contexte d'extraction K forme un ideal
d'ordre. Ainsi, chaque nceud du trie represente un generateur minimal. Ceci a
pour avantage de reduire la necessite en memoire centrale comparee a
l'utilisation d'un trie pour cha que ensemble de generateurs minimaux
de taille k donnee, comme c'est le cas pour les algorithmes CLOSE
[49], A-CLOSE [50] et TITANIC [57]. En effet, l'utilisation d'un seul trie
permet de reduire la redondance dans le stockage des informations relatives aux
generateurs minimaux. Cependant, le fait d'utiliser un seul trie rend l'espace
de recherche nettement plus grand lors de l'execution de quelques operations
telles que la verification de l'ideal d'ordre des generateurs minimaux
frequents oft la recherche des supports adequats dans la deuxieme etape de
l'algorithme PRINCE.
Un autre trie a ete utilise dans chaque iteration k,
de la premiere etape, afin de calculer le support des candidats generateurs
minimaux de taille k. La Figure 3.4 presente un trie qui
stocke quatre candidats generateurs minimaux de taille 3 : ABC, ABD, A CD et
BCD. Dans ce qui suit, nous donnons une presentation succincte de cette
structure de donnees.
Un trie est un arbre de recherche, dont les donnees sont
stockees d'une faZon condensee [12]. La structure de donnees trie etait a
l'origine introduite pour stocker et pour recuperer les mots d'un dictionnaire
[12]. Un trie est un arbre dirige du haut vers le bas comme dans le cas d'un
arbre de hachage. Neanmoins, dans le cas d'un trie, nous ne distinguons pas
entre un nceud interne et un nceud feuille contrairement au cas d'un arbre de
hachage. En effet, dans ce dernier, le nceud interne est caracterise par une
table de hachage et un nceud feuille contient un ensemble d'itemsets [14]. Dans
un trie, la racine est consideree a une profondeur 0, et un nceud a une
profondeur d ne peut pointer qu'aux nceuds de profondeur d +
1. Un pointeur est appele aussi branche ou lien, et est etiquete par une
lettre. Si un nceud u pointe sur un nceud v, u est appele le parent de v et v
un enfant de u.
|
Regles informatives approximatives
|
|
R8 : Ø0,80
BE
|
R13 : E0,75 BC
|
|
R9 : Ø0,80
C
|
R14 : A0,66 BCE
|
|
R10 : C0,75 A
|
R15 : BC0,66
AE
|
|
R11 : C0,75 BE
|
R16 : CE0,66
AB
|
|
R12 : B0,75 CE
|
|
|
A
|
B
|
C
|
D
|
E
|
|
1
|
×
|
|
×
|
×
|
|
|
2
|
|
×
|
×
|
|
×
|
|
3
|
×
|
×
|
×
|
|
×
|
|
4
|
|
×
|
|
|
×
|
|
5
|
×
|
×
|
×
|
|
×
|
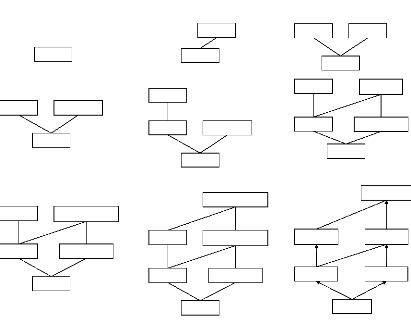
({C};4)
({B} ;4)
({B};4)
({0};5)
(b)
({0};5)
(a)
({0};5)
FIG . 3.1 -- Contexte d'extraction K
(c)
(e)
{AB} {AE}
({A};3)
({C};4)
({B} {E};4)
({0};5)
(g)
({AB} {AE};2)
({A};3)
({C};4)
({BC} {CE};3)
({B} {E};4)
({0};5)
(h)
({ABCE};2)
({AC};3)
({C};4)
{A} {BC} {CE}
{C}
{0}
({BCE};3)
({BE};4)
{B} {E}
({0};5)
(i)
({C};4)
({B} {E};4)
({C};4)
({B} {E};4)
({0};5)
(d)
({A};3)
({0};5)
({A};3)
({C};4)
({B} {E};4)
({0};5)
(f)
({BC};3)
({BC} {CE};3)
FIG . 3.2 -- Construction du treillis des generateurs minimaux et
le treillis d'Iceberg associes au contexte d'extraction K pour
minsup2.

R1 : EB
R2 : BE
R3 : AC
R4 : BCE
R5 : CEB
R6 : ABCE
R7 : AEBC
Regles informatives exactes
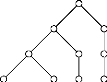
A B
B C
C D
D
C
D
FIG . 3.4 -- Exemple d'un trie
Chaque feuille l represente un mot qui est la concatenation
des lettres qui se trouvent sur le chemin de la racine a l. Notons que si les
premieres k lettres sont les memes pour deux mots, alors les
premieres k branches sur leurs chemins sont aussi les memes [12].
La structure de donnees trie permet de stocker et de recuperer
non seulement les mots mais n'importe quel ensemble E fini et ordonne.
Dans ce cas, chaque lien est etiquete par un element de E et le trie
contient un sous-ensemble F de E s'il y a un chemin oft les
liens sont etiquetes par les elements de F dans l'ordre choisi.
Dans notre contexte, l'alphabet est l'ensemble (ordonne) des
items I. Un k-itemset c :
{i1 < i2 <
i3 < . . . < ik} peut etre vu comme
etant le mot i1i2i3 ...ik
compose des lettres de I. Ainsi, le chemin menant de la racine a
chaque nceud du trie represente un (candidat) generateur minimal.
Plusieurs travaux ont etudie la structure de donnees trie.
Nous mentionnons principalement les travaux de Bodon et al. Dans [14], Bodon et
al. montrent l'interêt de l'utilisation de cette structure de donnees
comparee a la structure de donnee d'arbre de hachage en considerant differents
criteres, tels que la simplicite d'utilisation, l'extraction des informations,
etc. Dans [12, 13], Bodon montre l'efficacite de la structure trie, appliquee
à l'algorithme APRIORI [2], le premier a avoir introduit l'utilisation
de l'arbre de hachage, durant l'etape de calcul des supports des itemsets.
3.4 Preuves theoriques
Dans cette section, nous allons montrer la validite de
l'algorithme PRINCE. Ensuite, nous allons prouver la terminaison et la
completude de l'algorithme PRINCE.
Proposition 5 L'algorithme PRINCE est valide. En effet, il
permet de déterminer tous les itemsets fermés fréquents,
leurs générateurs minimaux associés ainsi que toutes les
règles généri ques informatives valides.
Preuve.
Nous allons montrer la validité de PRINCE en montrant la
validité de chacune des étapes le constituant.
1. Première étape : Détermination des
générateurs minimaux
PRINCE détermine tous les générateurs
minimaux fréquents et la bordure négative des
générateurs minimaux. En effet, PRINCE parcourt l'espace de
recherche par niveau (et donc par taille croissante des candidats
générateurs minimaux). Tout au long de ce parcours, PRINCE
élimine un candidat g de taille k ayant un de ses
sous-ensemble de taille (k-1), disons g1,
vérifiant une des deux conditions suivantes :
(a) g1 n'est pas un générateur minimal
fréquent alors, d'après la propriété d'idéal
d'ordre des générateurs minimaux fréquents (cf.
Proposition 1 page 24), g ne pourra pas être un
générateur minimal fréquent.
(b) g1 a un support égal a celui de
g. Ce dernier ne pourra pas être un générateur minimal
car il existe un sous-ensemble de g (en l'occurrence
g1) ayant la même fermeture que g (cf. Lemme 1
page 46).
Si aucune de ces deux conditions n'est
vérifiée, g est un générateur minimal.
S'il est fréquent, il sera introduit lors de la deuxième
étape dans le treillis des générateurs minimaux. Si
g est infréquent, g appartient a la bordure
négative des générateurs minimaux. En effet, tous les
sous-ensembles de g sont des générateurs minimaux
fréquents et g sera alors utilisé dans le
mécanisme de comptage par inférence utilisé lors de la
deuxième étape.
2. Deuxième étape : Construction du treillis des
générateurs minimaux
Le résultat de cette étape est le treillis des
générateurs minimaux. Cette étape per-met, d'une part, de
déterminer la classe d'équivalence adéquate relative a
chaque générateur minimal fréquent. D'autre part, elle
permet de trouver tous les successeurs immédiats d'une classe
d'équivalence. Montrons que cette étape est valide. Chaque
générateur minimal g est introduit dans le treillis des
générateurs minimaux via sa comparaison avec les listes des
successeurs immédiats des classes d'équivalence aux quelles
appartiennent ses sous-ensembles de taille (k-1). En effet, au moment
de l'introduction de g, les classes d'équivalence de ses
sous-ensembles de taille (k-1) ont déjà
été introduites dans le treillis des générateurs
minimaux. Ceci est dii au fait que le support des générateurs
minimaux fréquents composant chacune de ces classes d'équivalence
est strictement supérieur a celui de g. Ainsi, la fonction
REPRESENTANT permet de retrouver, pour chacun de ses sous-ensembles, disons
g1, le
representant de Cg1 et donc le generateur
minimal frequent oft est stockee la liste L des successeurs immediats
de Cg1 0). Lors des comparaisons de g
avec L, deux cas sont a distinguer (cf. Proposition 3 page 47) :
(a) Si g est compare avec le representant R
de Cg, les comparaisons avec les elements de L
s'arretent. Ensuite, la fonction GESTION-CLASSE-EQUIV est executee. Elle
remplace toutes les occurrences de g par R, dans les listes
des successeurs immediats oft g a ete ajoute. Ceci permet de n'avoir
que des representants dans les listes des successeurs immediats et n'affecte en
rien le resultat de la deuxieme etape, etant donne que g et R
appartiennent a la meme classe d'equivalence. Pour la meme raison - n'avoir que
des representants dans les listes des successeurs immediats - les comparaisons
a faire avec g seront effectuees avec R.
(b) Si g est un successeur d'un des elements de
L, disons g2, g sera compare aux elements de
la liste des successeurs de Cg2. Pour chaque
element g3 appartenant au reste des elements de
L, g ne pourra etre qu'un successeur de
Cg3. En effet, le cas (a) ne peut avoir lieu car
sinon g ne serait pas un successeur de g2.
Si aucun de ces deux cas ne se presente, g est un
successeur immédiat de g1 et est ajoute a L
et ne sera plus enleve(6). Cet ajout est valide etant donne que si
un generateur minimal frequent, disons h, est compare dans la suite
a g, alors h ne peut que verifier qu'un des deux cas (a) ou
(b) si Ch et Cg sont comparables (cad h ?
Cg ou Ch est un successeur de Cg).
En effet, h a un support inferieur ou egal = celui de g.
Ainsi, chaque liste des successeurs immediats est comparee a
tous les generateurs minimaux frequents susceptibles d'y appartenir. Les
traitements s'arrêtent lorsqu'il n'y a plus de generateurs minimaux
frequents a introduire dans le treillis des générateurs
minimaux.
3. Troisième étape : Extraction des bases
générigues informatives de règles
Dans cette etape, le parcours du treillis des
générateurs minimaux se fait en partant de Co. Montrons
que cette etape est valide. Toute classe d'equivalence autre que Co
admet au moins un predecesseur immediat et sera donc incluse dans au moins
une liste des successeurs immediats d'une autre classe d'equivalence. Ceci
permettra de
5Comme mentionné précédemment,
les générateurs minimaux fréquents autres que les
représentants
ont des listes de successeurs immédiats vides.
6Eventuellement, g ne pourra qu'être
remplacé par le représentant de Cg.
l'inclure dans la liste des classes d'équivalence a
traiter lors de la prochaine itération (cad dans la liste L2
de l'algorithme 4 page 53). Les traitements s'arrêtent lorsque la (resp.
les) liste(s) des successeurs immédiats de la (resp. des) classe(s)
d'équivalence traitée(s) en dernier est (resp. sont) vide(s).
Ainsi, toutes les classes d'équivalence seront traitées. En
appliquant la proposition 4 (cf. page 51), tous les itemsets fermés
fréquents sont retrouvés au fur et a mesure de ce parcours
ascendant et les regles génériques informatives valides sont
alors extraites d'une maniere directe.

Proposition 6 L'algorithme PRINCE termine et son résultat
est complet.
Preuve.
Montrons que l'algorithme PRINCE termine quel que soit le
contexte d'extraction 1C donné en entrée et quelles que
soient les valeurs de minsup et minconf. Etant donné que le nombre de
couples du contexte d'extraction est fini, le nombre de
générateurs minimaux fréquents extraits du contexte
1C lors de la premiere étape, et qui est donc a traiter lors de la
deuxieme étape, est aussi fini. De même, le treillis des
générateurs minimaux a parcourir lors de la troisieme
étape a une taille finie, égale au nombre de classes
d'équivalence.
Le résultat de l'algorithme PRINCE est complet
étant donné que la construction du treillis des
générateurs minimaux assure l'exhaustivité des
éléments (les générateurs minimaux
fréquents) de chaque classe d'équivalence. De même, elle
assure l'exhaustivité des éléments de la liste des
successeurs immédiats de chaque classe d'équivalence. Les
traitements effectués lors de la troisieme étape prennent ainsi
en compte toutes les classes d'équivalence et le résultat est
donc complet.

3.5 Complexite
Dans cette section, nous allons étudier la
complexité théorique au pire des cas de l'algorithme PRINCE.
Soit un contexte d'extraction 1C = (O, Z,
7Z), le pire des cas est obtenu quand le nombre de
générateurs minimaux fréquents est égal au nombre
d'itemsets fréquents et est égal au nombre d'itemsets
fermés fréquents (cad 2111) . En d'autres
termes, chaque générateur
minimal frequent est aussi un ferme et le treillis des
generateurs minimaux se confond avec le treillis des itemsets frequents.
Soient m=1O1 et n=1I1. La
taille maximale d'une transaction est egale au nombre maximum d'items
distincts, cad n. Nous allons considerer que toutes les transactions
ont pour longueur n. Pour chaque transaction et dans le pire des cas,
nous determinons ses 2n sous-ensembles afin de calculer les
supports des itemsets. Nous allons calculer la complexite theorique au pire des
cas de l'algorithme PRINCE en calculant la complexite au pire des cas de
chacune des trois etapes le constituant.
Premiere etape : Determination des generateurs minimaux
1. L'initialisation de l'ensemble des items candidats se fait
en O(1) (ligne 3 dans Algorithme 1 page 43).
2. Le cofit du calcul des supports des items est de l'ordre
de O(m × n) (ligne 4).
3. Les affectations des lignes 5-6 se font en O(1).
4. Le cofit de l'elagage par rapport aux supports des items est
de l'ordre de O(n) (lignes 7-15).
5. Le cofit de la determination des generateurs minimaux
frequents de tailles superieures ou egales a 2 (lignes 16-17) est egal a la
somme des cofits suivants :
(a) APRIORI-GEN : il y a (2n - n -
1) candidats a generer. Ainsi, le cofit de cette phase est de l'ordre de
O(2n - n) (lignes 3-4 dans Algorithme 2 page
44) ;
(b) Le cofit de la verification de l'ideal d'ordre, et en
meme temps, le calcul du support estime et le stockage des liens vers les
sous-ensembles adequats est de l'ordre de O(n2
× (2n - n)) (lignes 5-14) ;
(c) Le cofit du calcul des supports des candidats de tailles
superieures ou egales a 2 est de l'ordre de O(m ×
(2n - n)) (ligne 16) ;
(d) Le cofit de l'elagage par rapport aux supports des candidats
est de l'ordre de O(2n - n) (lignes
17-22).
La complexite Cl de cette etape est alors
: Cl = O(m × n + n +
(2n - n) + n2 ×
(2n - n) + m ×
(2n - n) + 2n - n)
= O(m × 2n + 2n
+ (n2 + 1) × (2n - n)).
Etant donne que 2n est largement superieur
a n, alors Cl =
O(m×2n+2n+(n2+1)×2n)
: O(m × 2n + (n2 + 2)
× 2n) = O(m × 2n +
n2 × 2n) :O((n2 +
m) × 2n).
D'ofi, C, = O((n2 +
m) × 2n).
G Deuxieme etape : Construction du treillis des generateurs
minimaux
1. La boucle pour de la ligne 3 (dans Algorithme 3 page 50) se
repetent 2n fois etant donne que dans le pire des cas, nous
avons 2n generateurs minimaux frequents.
2. Pour chaque generateur minimal frequent g de
taille k, la boucle pour de la ligne 4 se repete k fois etant
donne que g admet k sous-ensembles de taille (k-1)
(k, le nombre de sous-ensembles, sera largement majore
par n). Pour chaque sous-ensemble de g de taille
(k-1), disons g1, les traitements suivants sont
realises :
(a) Le coUt de l'instruction de la ligne 5 est en
O(1) etant donne que dans le pire des cas, g1 est le
seul generateur minimal frequent de sa classe d'equivalence et est donc son
representant (g1 est egal a R).
(b) La boucle pour de la ligne 6 se repete au maximum
(n-k) fois. En effet, g1, etant de taille
egale a (k-1), possede au maximum n - (k - 1)
- 1 successeurs immediats, au moment de l'integration de g dans
le treillis des generateurs minimaux ((n-k), le
nombre maximal de successeurs immediats, sera largement majore par n).
Dans chaque iteration de cette boucle, g est compare a un element
de g1.succs-immediats , disons g2. Le
coUt de la comparaison de g avec g2 est la somme
des deux coUts suivants :
i. Le premier coUt est relatif a l'union de g et
g2 et est, au pire des cas, de l'ordre de
O(n). Soit q, l'itemset resultat de cette union.
ii. Le second coUt est relatif a la recherche du support
adequat de q et est, au pire des cas, de l'ordre de
O(n). Notons que l'itemset q est un generateur minimal
frequent. En effet, q est inclus dans l'itemset contenant tous les
items, cad l'itemset I. Or, ce dernier -- dans le pire des cas -- est
un generateur minimal frequent et d'apres la propriete de l'ideal d'ordre des
generateurs minimaux frequents (cf. Proposition 1 page 24), q est un
generateur minimal frequent.
Etant donne que l'union de g avec tout element de
g1.succs-immediats donne toujours un generateur
minimal, aucune des deux conditions specifiees par la proposition 3 (cf. page
47) n'est verifiee (ces conditions sont decrites par les lignes 7-12).
Ainsi, Cg est incomparable avec toutes les classes
d'equivalence des representants appartenant a
g1.succs-immediats . g est donc ajoute a cette liste
en O(1) (lignes 13-14).
Ainsi, la complexite C2 de cette etape est de
l'ordre de : C2 = O(2n
× n × (1 + (n ×
(n + n)) + 1)) =
O(2n × n × (n ×
(n + n))).
D'oft, C2 =
O(n3 × 2n).
Troisieme etape : Extraction des bases generigues informatives de
regles
1. Le cofit des initialisations des lignes 3-6 (dans Algorithme
4 page 53) se fait en
O(1).
2. La condition de la boucle tant que est verifiee tant qu'il
y a des classes d'equivalence a traiter (ligne 7). Dans le pire des cas, chaque
generateur minimal frequent ferme forme une classe d'equivalence. Ainsi,
2n classes d'equivalence sont traitees. Pour chaque classe
d'equivalence C (ligne 8), le coilt total de cette etape est egal a la
somme des deux cofits suivants :
(a) Le premier cofit consiste a deriver la fermeture
correspondante a C. Cette derniere est le resultat de l'union du
generateur minimal frequent de C avec la fermeture d'un de ses
predecesseurs immediats (lignes 12-14). Ceci est realise, au pire des cas,
en O(n).
(b) Le deuxieme cofit est relatif a l'extraction des regles
d'association informatives.
i. Etant donne que, le generateur minimal frequent de
C est egal A sa fermeture, la condition de la ligne 9, testee en
O(1), n'est pas verifiee. Ainsi, aucune regle exacte informative n'est
extraite (ligne 10).
ii. Soit k la taille de l'itemset ferme frequent
de C. C possede alors k predecesseurs immediats.
Ainsi, pour une valeur de minconf egale a 0, k regles approximatives
informatives valides sont extraites (lignes 15-16). Le cont de l'extraction de
chacune des regles approximatives est egal au cont du calcul de la difference
entre la premisse et la conclusion et est, au pire des cas, de l'ordre de
O(n).
Le cont total, pour chaque classe d'equivalence, est alors de
l'ordre de O(n+
1 + n × n) (la taille
k d'un itemset ferme frequent etant largement majoree
par n).
La complexite C3 de cette etape est alors de
l'ordre de : C3 = O(1 + (n+ 1
+n2)×2n).
D'oft, C3 =
O(n2 × 2n).
Au pire des cas, la complexite totale de l'algorithme PRINCE est
de l'ordre de :
Cpire = C1 -h C2 -h
C3 = O((n2 + m)
× 2n) -h O(n3
× 2n) -h O(n2
× 2n) = O((n3 +
2 × n2 + m)2n) =
O((n3 + m) ×
2n).
D'oft, Cpire = O((n3 +
m) × 2n).
Ainsi, la complexite de PRINCE est de même ordre de
grandeur que celle des algorithmes dedies a l'extraction des itemsets fermes
frequents [29, 47], bien qu'il determine les trois composantes necessaires a
l'extraction des bases generiques de regles d'association.
3.6 Conclusion
Dans ce chapitre, nous avons introduit un nouvel algorithme,
appele PRINCE, pour l'extraction des bases generiques de regles. L'algorithme
PRINCE determine les generateurs minimaux frequents. Ensuite, il les ordonne
partiellement sous la forme d'un treillis des generateurs minimaux. Un balayage
de bas en haut de cette structure permet de retrouver les itemsets fermes
frequents et d'extraire les regles d'association informatives. Des preuves
theoriques ainsi qu'une etude de la complexite theorique relatives au nouvel
algorithme ont ete proposees.
Dans le chapitre suivant, nous allons essayer d'evaluer
experimentalement notre algorithme sur la base d'une serie de tests. Ces tests
permettront de voir l'influence de quelques optimisations que nous
introduisons, d'analyser les caracteristiques de notre algorithme, ainsi que de
comparer ses performances aux algorithmes d'exploration par niveau
existants.
Chapitre 4
Etude expérimentale
4.1 Introduction
Dans le chapitre précédent, nous avons introduit
un nouvel algorithme, appelé PRINCE, pour l'extraction des itemsets
fermés fréquents, leurs générateurs minimaux
associés ainsi que les regles génériques informatives
valides. A cet effet, PRINCE se distingue par la construction de la relation
d'ordre partiel contrairement aux algorithmes existants. Cette relation d'ordre
partiel est maintenue entre les générateurs minimaux
fréquents sous forme d'une structure partiellement ordonnée
appelée treillis des générateurs minimaux. A partir de
cette structure, l'extraction des regles génériques informatives
valides devient immédiate.
Dans ce chapitre, nous présentons quelques
optimisations apportées a notre algorithme et nous mesurons leurs
impacts sur les performances de l'algorithme PRINCE 1. Ensuite, nous
présentons une évaluation expérimentale - menée sur
des bases benchmark et des bases "pire des cas" - permettant d'analyser les
caractéristiques de l'algorithme PRINCE et de comparer ses performances
a celles des algorithmes CLOSE, A-CLOSE et TITANIC. Ces derniers se limitent a
extraire les itemsets fermés fréquents et leurs
générateurs minimaux seulement. Leurs codes sources ont
été mis a notre disposition par Yves Bastide.
4.2 Environnement d'experimentation
4.2.1 Environnement materiel et logiciel
Toutes les experimentations ont ete realisees sur un P C muni
d'un processeur Pentium IV ayant une frequence d'horloge de 2,4 GHz et 512 Mo
de memoire RAM (avec 2 Go d'espace d'echange ou Swap) tournant sous la
plate-forme SuSE Linux 9.0. PRINCE est implante en Langage C tandis que CLOSE,
A-CLOSE et TITANIC le sont en C-h-h. Les programmes ont ete compiles avec le
compilateur gcc 3.3.1.
4.2.2 Description des executables
Dans le cadre de nos experimentations, nous avons utilise les
executables decrits par le tableau 4.1.
|
Algorithme(s)
|
Entrée
|
Sortie
|
|
PRINCE
|
Fichier ascii (.dat), minsup, mincon~.
|
Les itemsets fermes frequents, leurs generateurs minimaux
associes ainsi que les bases generiques de regles.
|
|
CLOSE, A-
CLOSE et
TITANIC
|
Fichier binaire
(.bam), minsup.
|
Les itemsets fermes frequents et leurs generateurs minimaux
associes.
|
TAB . 4.1: Description des executables des differents
algorithmes
4.2.3 Bases de test
Dans le cadre de nos experimentations, nous avons comptabilise
le temps d'execution total des algorithmes sur des bases benchmark ainsi que
sur des bases "pire des cas". Tout au long de ce chapitre, les figures
presentees ont une echelle logarithmique.
4.2.3.1 Bases benchmark
Les bases benchmark sont divisees en des bases denses et des
bases eparses (2). Les caracteristiques de ces bases sont resumees
par le tableau 4.3. Ce tableau definit, pour chaque base, son type, le nombre
de transactions, le nombre d'items et la taille moyenne des
2L'ensemble de ces bases est disponible a l'adresse
suivante : http ://
fimi.cs.helsinki.fi/data.
transactions. La base PUMSB contient des données de
recensement (cad des données statistiques). La base MUSHROOM contient
les caractéristiques de diverses espèces de champignons. Les
bases CONNECT et CHESS sont dérivées a partir des étapes
de jeux respectifs qu'elles représentent. Ces bases sont fournies par U
C Irvine Machine Learning Database Repository (3). Typiquement, ces
bases sont très denses (cad elles produisent plusieurs itemsets
fréquents longs même pour des valeurs de supports
élevées). T10I4D100K et T40I10D100K sont deux bases
synthétiques générées par un programme
développé dans le cadre du projet dbQUEST (4). Ces
bases simulent le comportement d'achats des clients dans des grandes surfaces
[36]. Le tableau 4.2 présente les différents paramètres
des bases synthétiques. La base RETAIL [17] est fournie par une grande
surface anonyme située en Belgique. La base ACCIDENTS [28] est obtenue
de l'institut national belge de statistiques et représente des
statistiques sur les accidents du trafic survenus dans la région de
Flandre (Belgique) entre 1 991 et 2 000.
|
|T|
|
Taille moyenne des transactions
|
|
|I|
|
Taille moyenne des itemsets maximaux potentiellement
fréquents
|
|
|D|
|
Nombre de transactions générées
|
TAB . 4.2 -- Paramètres des bases synthétiques
|
NOM DE
LA BASE
|
TYPE DE LA BASE
|
NOMBRE DE TRANSACTIONS
|
NOMBRE D'ITEMS
|
TAILLE MOYENNE DES TRANSACTIONS
|
|
PUMSB
|
Dense
|
49046
|
7 117
|
74
|
|
CONNECT
|
Dense
|
67 557
|
129
|
43
|
|
CHESS
|
Dense
|
3 196
|
75
|
37
|
|
MUSHROOM
|
Dense
|
8 124
|
119
|
23
|
|
T10I4D100K
|
Eparse
|
100 000
|
1 000
|
10
|
|
T40I10D100K
|
Eparse
|
100 000
|
1 000
|
40
|
|
RETAIL
|
Eparse
|
88 162
|
16 470
|
10
|
|
ACCIDENTS
|
Eparse
|
340 183
|
468
|
33
|
TAB . 4.3 -- Caractéristiques des bases benchmark
3http ://www.ics.uci.edu/~mlearn/ML
Repository.html .
4 Le generateur des bases synthetiques est disponible
a l'adresse suivante
http ://
www.almaden.ibm.com/software/quest/
Resources/datasets/data/ .
4.2.3.2 Bases "pire des cas"
Dans le cadre de nos experimentations, nous avons realise des
tests sur des bases "pire des cas". La configuration de chacune de ces bases
est une legère modification de celle presentee par Fu et Nguifo dans
[26]. La definition d'une base "pire des cas" est comme suit :
Definition 9 Une base "pire des cas" est une base oit la taille
de l'ensemble des items
I est égale a n et celle de
l'ensemble des transactions O est égale a (n+1). Dans
cette base, cha que item est vérifié par n transactions
différentes. Cha que transaction, parmi les n premières,
est vérifiée par (n-1) items différents. La
dernière transaction est vérifiée par tous les items. Les
transactions sont toutes différentes deux a deux. Les items sont tous
différents deux a deux.
|
i1
|
i2
|
i3
|
i4
|
|
1
|
|
x
|
x
|
x
|
|
2
|
x
|
|
x
|
x
|
|
3
|
x
|
x
|
|
x
|
|
4
|
x
|
x
|
x
|
|
|
5
|
x
|
x
|
x
|
x
|
FIG . 4.1 -- Exemple d'une base "pire des cas" avec
n4
La Figure 4.1 presente un exemple d'une base "pire des cas"
avec n egal a 4.
Une base "pire des cas" donne, pour une valeur de minsup egale
a 1, un treillis complet des itemsets frequents contenant 2' itemsets
frequents. Dans le pire des cas, le treillis des itemsets frequents se confond
avec le treillis des itemsets fermes frequents ainsi qu'avec le treillis des
générateurs minimaux.
L'algorithme BASE-PIRE-CAS, dont le pseudo-code est donne par
l'algorithme 5, permet de generer une base "pire des cas" dans un fichier F et
pour une valeur n donnee.
4.3 Optimisations et evaluations
1 Algorithme : BASE-PIRE-CAS
Donnees : - Un entier n.
Resultats : - Un fichier F contenant une base "pire des cas" de
dimension (n + 1)×n.
2 debut
3
4
5
6
7
8
pour (i--1; i < n; i++) faire pour
(j--1 ; j < n; j++) faire
si i =~ j alors

écrire(F,i);
pour (i--1; i < n; i++) faire

écrire(F,i);
9 fin
Algorithme 5 : BASE-PIRE-CAS
nombre de comparaisons. Dans toutes les figures qui vont suivre,
nous utilisons une valeur de minconf égale a 0 (cad toute regle
générique extraite est valide).
1. Representation compacte de la base : lors de la premiere
étape et afin de réduire le cofit du calcul des supports des
candidats générateurs minimaux (cf. la procédure GEN-GMS
page 43), nous utilisons des techniques permettant de réduire la taille
de la base a traiter. Pour cela, nous introduisons une structure de
données appelée IT-BDT (Itemset-Trie-BaseDeTransaction). IT-BDT
est une modification de la structure de données Itemset-Trie [8]
permettant de stocker le contexte d'extraction en mémoire centrale et de
retrouver les items relatifs aux différentes transactions.
L'utilisation d'une structure interne pour stocker le contexte
d'extraction est adoptée par plusieurs travaux, tels que [12, 37, 62].
Dans la structure Itemset-Trie, le compteur que contient un nceud N
indique le nombre d'occurrences des transactions ayant en commun N.
Dans la figure 4.2 (Gauche), le nceud contenant l'itemset A possede un compteur
égal a 3 car c'est l'intersection de trois transactions, a savoir A CD,
AB CE et AB CE. Dans la structure IT-DBT, ce compteur prend pour valeur 0 si
les items se trouvant sur le chemin menant de la racine a N ne
représentent pas une transaction sinon le compteur prend pour valeur le
nombre de fois que la transaction s'est répétée dans la
base de transactions. Dans la figure 4.2 (Droite), le nceud contenant l'itemset
A a un compteur égal a 0 car A ne forme pas a lui seul une
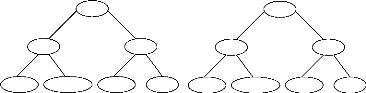
(CD,1) (BCE,2)
(A,3)
root
(CE,1) (E,1)
(B,2)
(CD,1) (BCE,2)
(A,0)
root
(CE,1) (E,1)
(B,0)
FIG . 4.2 -- La structure Itemset-Trie (Gauche) et la structure
IT-BDT (Droite) associees au contexte d'extraction de la Figure 3.1
transaction. De plus, le calcul du support des 1-itemsets se
fait en même temps que la construction de la structure IT-BDT. Notons que
la structure IT-BDT permet aussi de mettre en place un processus de fouille
interactif etant donne qu'il n'y a nul besoin de la reconstruire si nous
changeons la valeur de minsup, contrairement A d'autres structures telles que
FP-Tree [34, 35] et Patricia-Trie [53], etc. Afin de ne pas faire perdre a la
structure IT-DBT ce dernier avantage, nous n'eliminons, de cette structure, ni
les items infrequents ni ceux ayant même support que celui de l'ensemble
vide. Cependant, lors du parcours de cette structure, seuls les items frequents
de supports inferieurs a celui de l'ensemble vide (cad les items generateurs
minimaux frequents) seront pris en compte. De plus, toute transaction ne
depassant pas la taille des candidats n'est pas prise en compte etant donne
qu'elle ne contient aucun candidat.
Evaluation experimentale de cette optimisation : Nous allons
tester une version de PRINCE oft nous utilisons une representation compacte de
la base comparee a une version oft la base a traiter se trouve sur le disque et
aucun traitement relatif aux transactions n'est effectue. Pour realiser ce
test, nous avons choisi les bases PUMSB, CONNECT et ACCIDENTS etant donne que,
pour ces bases, le calcul du support des candidats est une operation coliteuse
vu le nombre ainsi que la taille moyenne des transactions que contiennent ces
bases. Pour les trois bases sus-mentionnees, la figure 4.3 montre les temps
d'execution de PRINCE dans les deux cas : avec utilisation de la representation
compacte de la base (cf. courbe "avec RC") et sans utilisation de la
representation compacte de la base (cf. courbe "sans RC").
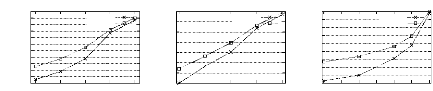
Temps d'execution (en seconde)
1024
256
512
128
64
32
16
8
90
80
Connect
70
60
50
Temps d'execution (en seconde)
4096
2048
1024
256
512
128
64
32
16
8
90
80
70
Accidents
60
avec Rc
sans Rc
50
40
30
Temps d'execution (en seconde)
4096
2048
1024
256
512
128
64
32
16
4
2
8
95
90
Pumsb
85
avec Rc
sans Rc
80
75
avec Rc
sans Rc
Minsup (en %) Minsup (en %) Minsup (en %)
FIG . 4.3 -- Effet de l'utilisation d'une représentation
compacte de la base sur les performances de PRINCE
tées (une réduction comprise entre 20,87% a
75,00% pour PUMSB, entre 10,84% et 61,90% pour CONNECT et entre 14,67% et
80,76% pour ACCIDENTS). Cette réduction diminue proportionnellement a la
baisse des valeurs de minsup. Ceci peut être expliqué par le fait
que plus la valeur de minsup baisse, moins il y a d'items infréquents.
D'oft, seule l'utilisation d'IT-BDT reste bénéfique pour les
performances de PRINCE.
2. Reduction du nombre de comparaisons : Afin de
réduire le nombre de comparaisons effectuées lors de la deuxieme
étape (cf. la procédure GEN-ORDRE page 50), nous avons
utilisé les optimisations suivantes :
(a) La premiere optimisation consiste a mettre en place un
traitement permettant de savoir si chaque générateur minimal
fréquent est aussi un fermé ou non. Ce même traitement est
utilisé dans l'algorithme A-CLOSE (cf. page 26). Dans le cas de ce
dernier, ce traitement indique a partir de quelle taille des
générateurs minimaux fréquents, il y aurait un calcul des
fermetures. Dans notre cas et a la fin de la premiere étape, ce
traitement permet d'indiquer si l'algorithme PRINCE nécessite ou non
d'exécuter la deuxieme étape. En effet, si chaque
générateur minimal fréquent est aussi un fermé, le
treillis des générateurs minimaux est construit des la premiere
étape et l'algorithme PRINCE n'a pas a exécuter la
procédure GEN-ORDRE. Un simple parcours de l'ensemble
est alors suffisant. Il n'y alors pas de regle exacte
informative. Etant donné que nous stockons dans le champ
sous-ens-directs, des liens vers les sous-ensembles de taille (k-1) de
tout générateur minimal g de taille k, nous
avons les prémisses nécessaires pour extraire les regles
approximatives informatives valides.
version de PRINCE oft la procédure GEN-ORDRE est
exécutée, bien que chaque générateur minimal
fréquent est aussi un fermé, comparée a une version oft
cette procédure n'est pas exécutée. Pour réaliser
ce test, nous allons utiliser la base ACCIDENTS étant donné que
pour des valeurs de minsup supérieures ou égales a 40%, chaque
générateur minimal fréquent est un fermé. La figure
4.4 montre les temps d'exécution de PRINCE dans les deux cas : avec
exécution de GEN-ORDRE (cf. courbe "avec G-O") et sans exécution
de GEN-ORDRE (cf. courbe "sans G-O").
Temps d'execution (en seconde)
256
128
64
32
16
8
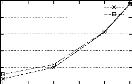
90
80
Accidents
70
avec G-O
sans G-O
60
50
40
Minsup (en %)
FIG . 4.4 -- Effet de l'exécution de la procédure
GEN-ORDRE sur les performances de PRINCE
Le fait de ne pas exécuter la procédure GEN-ORDRE
permet de réduire les temps d'exécution de PRINCE de 2,23%
jusqu'a 16,66%.
(b) La deuxième optimisation consiste a utiliser les
2-itemsets fréquents non générateurs minimaux pour
déterminer la relation entre les items fréquents. Ces items ont
tous un sous-ensemble commun a savoir l'ensemble vide. Soit Z un
itemset fréquent non générateur minimal et soient
x et y les items le composant. En comparant le support de
Z a ceux de x et y, nous pouvons connaitre la relation
entre Cx et Cy. Dans la premiere
étape de l'algorithme PRINCE, nous ajoutons donc un traitement qui, des
le calcul des supports des candidats générateurs minimaux de
taille 2, traite chaque 2-itemset fréquent non générateur
minimal pour déterminer la relation entre les classes
d'équivalence des items le composant. Le traitement d'un 2-itemset
générateur minimal Z, ne sert a rien puisque les classes
d'équivalence des items le composant sont incomparables (sinon Z,
ne serait pas générateur minimal). L'utilisation des
candidats générateurs minimaux de taille 2 est favorisée
par le fait que tous
ces candidats vérifient l'idéal d'ordre et nous
avons ainsi le support de toutes les combinaisons possibles, de taille 2,
d'items fréquents.
Evaluation expérimentale de cette optimisation : Afin
de tester l'effet de l'utilisation des 2-itemsets fréquents non
générateurs minimaux pour déterminer la relation entre les
items fréquents, nous allons utiliser la base RETAIL. En effet, dans
cette base, le nombre d'items est très élevé (16470
items). Ceci rend élevé le nombre de comparaisons entre les
1-itemsets fréquents pour de basses valeurs de minsup. La figure 4.5
montre les temps d'exécution de PRINCE dans les deux cas : prise en
compte des 2-itemsets fréquents non générateurs minimaux
(courbe "avec 2-freqs-Non-GMs") ou non (courbe "sans 2-freqs-Non-GMs").
Temps d'execution (en seconde)
4096
2048
1024
256
512
128
64
32
16
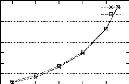
0.1
avec 2-freqs-Non-GMs
sans 2-freqs-Non-GMs
0.08
0.06
Retail
0.04
0.02
0
Minsup (en %)
FIG . 4.5 -- Effet de l'utilisation des 2-itemsets
fréquents non générateurs minimaux sur les performances de
PRINCE
L'utilisation des 2-itemsets fréquents non
générateurs minimaux permet de
réduire les temps d'exécution de PRINCE de 1,71%
jusqu'a 13,79%.
(c) La troisième optimisation consiste a stocker, pour
chaque générateur minimal fréquent g, une liste
prohibée notée lg, des
générateurs minimaux fréquents auxquels nous avons
comparé g a leurs listes de successeurs immédiats. Ceci
permet d'éviter de comparer g a une liste des successeurs
immédiats L plus qu'une fois étant donné que les
comparaisons qui en découlent sont superflues. En effet, le
résultat de ces comparaisons est le même que celui de la
première comparaison de g avec L. La notion de liste
prohibée est étendue au niveau de la classe d'équivalence.
Ainsi, si g est comparé avec le représentant de sa
classe d'équivalence R., nous ajoutons les éléments de
lg a la liste prohibée de R. (cad lR)
étant donné que le reste des comparaisons est poursuivi avec ce
dernier.
Evaluation expérimentale de cette optimisation : Pour
tester l'effet de l'utilisation de la liste prohibée, nous utilisons la
base MUSHROOM. En effet, pour cette base, la construction de l'ordre partiel
est l'étape la plus coUteuse (le calcul du support est favorisé
par un nombre réduit de transactions de petite taille moyenne). La
figure 4.6 montre les temps d'exécution de PRINCE dans les deux cas :
utilisation des listes prohibés (courbe "avec listes prohibées")
ou non (courbe "sans listes prohibées").
Temps d'execution (en seconde)
1024
256
512
128
64
32
16
4
2
8
1
20
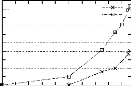
18
16
avec listes prohibees
sans listes prohibees
14
Mushroom
12
10
8
6
4
2
Minsup (en %)
FIG . 4.6 -- Effet de l'utilisation des listes prohibées
sur les performances de PRINCE
L'utilisation des listes prohibées permet
d'éviter l'exécution d'un grand nombre
de comparaisons non
nécessaires. Ainsi, nous constatons une réduction
signifi-
cative des temps d'exécution de PRINCE allant de 50,00% et
atteignant 97,47%.
Comme dans le cas du premier type d'optimisation, cad la
représentation compacte de la base, nous constatons que l'utilisation
des optimisations relatives a la réduction du nombre de comparaisons
réduit les temps d'exécution de PRINCE et s'adaptent aux
caractéristiques différentes des bases.
Il faut insister sur le fait, que pour chaque type
d'optimisations (cad la représentation compacte de la base ou la
réduction du nombre de comparaisons), les optimisations utilisées
se complètent l'une l'autre et ne s'excluent pas mutuellement.
4.4 Effets de la variation de la mesure minconf
Dans cette section, nous allons tester, pour une base
donnée, l'effet de la variation de la mesure minconf sur les
performances de PRINCE. La version utilisée dans ce test ainsi que dans
les expérimentations présentées dans le reste du chapitre
est une version dans laquelle toutes les optimisations sus-décrites sont
implémentées.
Pour évaluer l'effet de la variation de la valeur de
minconf, nous considérons deux cas extremes a savoir le cas oft la
valeur de minconf est égale a 0 (cad que toutes les regles
génériques sont valides) et le cas oft la valeur de minconf est
égale a 1 (cad que seules les regles génériques exactes
sont valides). Pour réaliser ce test, nous avons choisi les bases CHESS
et T40I10D100K étant donné le nombre élevé de
regles valides extraites de ces bases si la valeur de minconf est égale
a 0 et pour de faibles valeurs de minsup. La figure 4.7 montre les temps
d'exécution de notre algorithme sur ces deux bases pour une valeur de
minconf égale a 0 et pour une valeur de minconf égale a 1.
FIG . 4.7 -- Effet de la variation de minconf sur les
performances de PRINCE
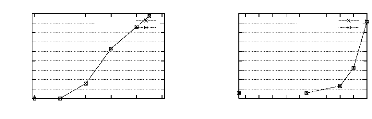
1024
512
Temps d'execution (en seconde)
512
256
256
128
Temps d'execution (en seconde)
128
64
32
64
16
32
8
16
4
8
2
4
1
2
90
0.5
50
60
70
80
Chess
minconf=0
minconf=1
40
Minsup (en %)
T40I10D100K
minconf=0
minconf=1
9.5 8.5 7.5 6.5 5.5 4.5 3.5 2.5 1.5
Minsup (en %)
Nous constatons que la variation de la valeur de minconf n'a
pas de conséquence significative sur les performances de PRINCE pour les
bases CHESS et T40I10D100K. Ce résultat n'est pas restreint a ces deux
bases mais est généralisable pour toutes les bases
testées. En effet, tout au long de nos expérimentations, nous
avons constaté qu'étant donné le treillis des
générateurs minimaux construit, la troisième étape
(cad la procédure GEN-BGRS page 53) constitue l'étape la moins
cofiteuse dans notre algorithme. De plus, la modification dans les valeurs de
minsup et celles de minconf, pour une valeur fixée de minsup, n'a pas
une influence significative sur les temps d'exécution de cette
étape.
4.5 Comparaisons des coilts des &tapes de
PRINCE
Dans cette section, nous allons comparer les temps
d'exécution des étapes constituant l'algorithme PRINCE. Rappelons
que l'algorithme PRINCE est constitué de trois étapes, a savoir
:
1. Détermination des générateurs minimaux
(cf. la procédure GEN-GMS page 43) ;
2. Construction du treillis des générateurs
minimaux (cf. la procedure GEN-ORDRE page 50) ;
3. Extraction des bases generiques informatives de regles (cf.
la procedure GEN-BGRS page 53).
4.5.1 Bases benchmark
Dans toutes les figures qui vont suivre, et pour l'algorithme
PRINCE, nous utilisons une valeur de minconf egale a 0 (cad que nous avons
considere, pour une valeur de minsup fixee, le pire des cas par rapport au
nombre de regles generees). Les comparaisons des etapes constituant PRINCE
seront divisees en deux parties :
G Comparaisons sur des bases denses ;
G Comparaisons sur des bases eparses.
4.5.1.1 Comparaisons sur les bases denses
Les temps d'execution des differentes etapes de l'algorithme
PRINCE sur les bases denses sont presentes par la figure 4.8 et le tableau
4.4.
- PUMSB et CONNECT : ces deux bases sont caracterisees par un
nombre ainsi qu'une taille moyenne des transactions relativement eleves. Ces
caracteristiques influent enormement sur la repartition du temps d'execution
total de l'algorithme PRINCE par rapport aux trois etapes le constituant.
Ainsi, la premiere etape, cad la determination des generateurs minimaux, est
l'etape la plus coUteuse pour ces deux bases. La deuxieme et troisieme etape
n'ont pas une influence significative sur les temps d'execution de PRINCE. En
effet, pour la base PUMSB (resp. CONNECT), les temps d'execution de ces deux
etapes ne depassent pas 1,28% (resp. 3,01%) du temps d'execution total de
l'algorithme PRINCE.
- CHESS : cette base est caracterisee par un nombre reduit de
transactions. Cependant, la taille moyenne des transactions est elevee, ce qui
influe sur les temps d'execution de la premiere etape. D'autant plus, CHESS
permet d'extraire un nombre eleve de generateurs minimaux frequents atteignant
719 886 pour minsup 45%. Ce nombre maintient la premiere etape comme etant la
plus cofiteuse. Le temps d'execution relatif a la construction du treillis des
générateurs minimaux est lui aussi influence par le nombre de
generateurs minimaux frequents extraits lors de la premiere etape. La troisieme
etape, cad l'extraction des bases generiques de regles, est la moins cofiteuse.
En effet, le temps d'execution de cette etape ne depasse pas 2,06% du temps
d'execution total de l'algorithme PRINCE.
- MUSHROOM : cette base est caracterisee par un nombre reduit
de transactions ainsi qu'une taille moyenne reduite des transactions. Ainsi, la
premiere etape ne pese pas lourd sur les performances de l'algorithme PRINCE.
Cependant, le nombre de generateurs minimaux frequents, atteignant 360 166 pour
minsup:0,1, extraits lors de cette premiere etape influe sur le temps
d'execution de la deuxieme etape. Ainsi, cette derniere est la plus coUteuse.
Il faut noter que comme pour les trois premieres bases, la troisieme etape n'a
pas une influence significative sur les temps d'execution de l'algorithme
PRINCE. Son temps d'execution ne depasse pas 10% du temps d'execution total.
Ces comparaisons confirment que, etant le treillis des
générateurs minimaux construit, l'extraction des bases generiques
de regles devient immediate et n'a pas d'influence notable sur les performances
de l'algorithme PRINCE.
Temps d'execution (en seconde)
4096
1024
256
64
16
4
1
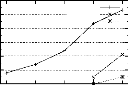
95
90
Pumsb
85
étape 1
étape 2
étape 3
80
75
Temps d'execution (en seconde)
1024
256
512
128
64
32
16
4
2
8
1
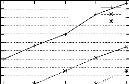
90
80
Connect
70
étape 1
étape 2
étape 3
60
50
Minsup (en %)
Temps d'execution (en seconde)
256
128
64
32
16
4
2
8
1
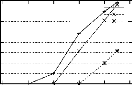
90
80
70
Chess
60
étape 1
étape 2
étape 3
50
40
Minsup (en %) Minsup (en %)
Temps d'execution (en seconde)
64
32
16
4
2
8
1
20
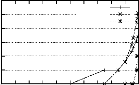
18
16
14
Mushroom
12
10
étape 1
étape 2
étape 3
8
6
4
2
0
Minsup (en %)
FIG . 4.8 -- Temps d'execution des etapes constituant PRINCE pour
les bases denses
4.5.2.1 Comparaisons sur les bases eparses
Les temps d'execution des differentes etapes de l'algorithme
PRINCE sur les bases eparses sont presentes par la figure 4.9 et le tableau
4.5.
|
Base
|
minsup
|
Temps d,exécution total
|
1i`ere étape
|
2i`eme étape
|
3i`eme étape
|
|
PUMSB
|
95,00%
|
3
|
3
|
0
|
0
|
|
90,00%
|
7
|
7
|
0
|
0
|
|
85,00%
|
27
|
27
|
0
|
0
|
|
80,00%
|
416
|
413
|
2
|
1
|
|
75,00%
|
1 641
|
1 620
|
19
|
2
|
|
CONNECT
|
90,00%
|
8
|
8
|
0
|
0
|
|
80,00%
|
25
|
24
|
1
|
0
|
|
70,00%
|
66
|
63
|
3
|
0
|
|
60,00%
|
332
|
322
|
9
|
1
|
|
50,00%
|
847
|
822
|
22
|
3
|
|
CHESS
|
90,00%
|
1
|
1
|
0
|
0
|
|
80,00%
|
1
|
1
|
0
|
0
|
|
70,00%
|
3
|
2
|
1
|
0
|
|
60,00%
|
39
|
29
|
9
|
1
|
|
50,00%
|
197
|
124
|
69
|
4
|
|
45,00%
|
435
|
230
|
196
|
9
|
|
MUSHROOM
|
20,00%
|
1
|
1
|
0
|
0
|
|
10,00%
|
1
|
1
|
0
|
0
|
|
5,00%
|
3
|
2
|
1
|
0
|
|
3,00%
|
4
|
2
|
2
|
0
|
|
2,00%
|
7
|
3
|
3
|
1
|
|
1,00%
|
13
|
5
|
7
|
1
|
|
0,80%
|
17
|
6
|
10
|
1
|
|
0,30%
|
33
|
9
|
22
|
2
|
|
0,20%
|
40
|
10
|
26
|
4
|
|
0,10%
|
50
|
11
|
35
|
4
|
transactions reduite (10 items). Pour des valeurs de minsup
superieures ou egales a 0,5%, chaque generateur minimal frequent est aussi un
ferme. L'algorithme PRINCE n'execute donc pas sa deuxieme etape. Cependant, ce
n'est plus le cas pour des supports inferieurs A 0,5%. Le temps d'execution de
la deuxieme etape croit alors proportionnellement au nombre de generateurs
minimaux extraits lors de la premiere etape. Il est important de noter que la
construction de l'ordre partiel est influence par l'augmentation de la taille
de la bordure negative des generateurs minimaux
GBd-. En effet, dans le cas des bases eparses, le
treillis des itemsets frequents tend a se confondre avec le treillis des
generateurs minimaux. Ainsi, la quasi-totalite des itemsets sont des
generateurs minimaux. Grace a la metrique statistique minsup, ces itemsets sont
consideres generalement comme infrequents. Cette augmentation dans la taille de
la bordure negative GBd- induit une augmentation
dans l'espace de recherche des supports adequats lors de la construction de
l'ordre partiel. La troisieme etape presente un temps d'execution negligeable
etant donne que le nombre de generateurs minimaux frequents extraits reste
reduit meme pour des valeurs tres basses de minsup. Pour minsup=0,02, le nombre
de generateurs minimaux frequents est egal a 109 940.
- T4 O!1 OD1 OOK : cette base est caracterisee par un nombre
eleve de transactions ainsi qu'une taille moyenne des transactions elevee (40
items). Ainsi, la premiere etape s'avere la plus cofiteuse. Pour des valeurs de
minsup superieures ou egales a 1,5%, chaque generateur minimal frequent est
aussi un ferme et la deuxieme etape n'est pas executee. Pour des valeurs de
minsup inferieures a 1,5%, chaque generateur minimal frequent n'est plus un
ferme. De plus, le nombre de candidats generateurs minimaux augmente
considerablement en passant de minsup=1,5% a minsup=0,5%. En effet, pour
minsup=1,5%, le nombre de candidats generateurs minimaux est egal a 276 886
alors qu'il est egal a 3 452 429 pour minsup=0,5%. Ceci explique le saut dans
les temps d'execution de PRINCE entre ces deux valeurs de minsup. La troisieme
etape reste la moins cofiteuse. Son cofit ne depasse pas 2,74% du temps
d'execution total.
- RETAIL : comme c'est le cas pour la base T10I4D100K, la base
RETAIL est caracterisee par un nombre eleve de transactions et par une taille
moyenne reduite des transactions. La premiere etape est la plus coUteuse
comparee a la deuxieme et a la troisieme etape. La deuxieme etape est penalisee
par l'augmentation de la taille de la bordure negative des generateurs
minimaux GBd-. En effet, RETAIL est caracterisee
par un nombre eleve d'items et dont la quasi-totalite sont qualifies de
frequents avec les valeurs de minsup utilisees dans nos tests (pour
minsup=0,01%, 9 300 1-itemsets, parmi 16 470, sont frequents).
Ce nombre d'items fréquents entraine la
génération d'un nombre élevé de candidats et dont
la plupart sont infréquents. Ceci explique l'augmentation du temps
d'exécution de la deuxième étape en passant de
minsup=0,02% a minsup=0,01%. La troisième étape reste la moins
cofiteuse et son temps d'exécution est négligeable
comparativement aux deux premières étapes.
Il est intéressant de noter que pour une même
valeur de minsup égale a 0,5%, le temps d'exécution ainsi que le
nombre de générateurs minimaux fréquents extraits des
bases T10I4D100K et RETAIL sont comparables. En effet, le temps
d'exécution total est presque égal au temps d'exécution de
la première étape. De plus, le nombre de
générateurs minimaux fréquents extraits de T10I4D100K
(resp. RETAIL) est égal a 1 074 (resp. 582) pour une taille maximale
d'un générateur minimal fréquent égal a 6 (resp. 5)
items. Ces résultats peuvent être expliqués par un nombre
de transactions relativement proche pour ces deux bases, ainsi qu'une
même taille moyenne des transactions. Cependant, en comparant les
résultats de ces deux bases a ceux de la base T40I10D100K pour la
même valeur de minsup (cad 0,5%), nous (cad 0,5%), nous notons une
différence significative. En effet, le nombre de
générateurs minimaux fréquents extraits de la base
T40I10D100K pour cette valeur de minsup est égal a 1 276 055. Ceci
représente presque 1 188 (resp. 2 193) fois le nombre de
générateurs minimaux fréquents généré
dans T10I4D100K (resp. RETAIL). De même la taille maximale d'un
générateur minimal fréquent atteint 18 items. Ainsi, bien
que les trois bases T10I4D100K, T40I10D100K et RETAIL ont pratiquement le
même nombre de transactions, leurs tailles moyenne des transactions
expliquent la différence dans le nombre de générateurs
minimaux extraits. En effet, la taille moyenne des transactions dans le cas de
T40I10D100K, égale a 40 items, est quatre fois plus élevée
que celles des deux autres bases, égales a 10 items.
- ACCIDENTS : cette base est caractérisée par un
nombre très élevé de transactions avec une taille moyenne
importante. Ces caractéristiques ont pour conséquence le fait que
le temps d'exécution de la première étape domine le temps
d'exécution total de l'algorithme PRINCE. Il faut noter que pour des
valeurs de minsup supérieures ou égales a 40%, chaque
générateur minimal fréquent est aussi un fermé et
PRINCE n'a pas a exécuter sa deuxième étape. Comme pour
toutes les bases benchmark testées, la troisième étape,
cad l'extraction des bases génériques informatives de
règles, est la moins conteuse parmi les trois étapes constituant
l'algorithme PRINCE.
|
Base
|
minsup
|
Temps d,exécution total
|
1i`ere étape
|
2i`eme étape
|
3i`eme étape
|
|
T10I4D100K
|
0,50%
|
3
|
3
|
0
|
0
|
|
0,20%
|
4
|
4
|
0
|
0
|
|
0,10%
|
8
|
7
|
1
|
0
|
|
0,08%
|
10
|
9
|
1
|
0
|
|
0,05%
|
20
|
16
|
4
|
0
|
|
0,03%
|
50
|
35
|
15
|
0
|
|
0,02%
|
105
|
58
|
47
|
0
|
|
T40I10D100K
|
10,00%
|
3
|
3
|
0
|
0
|
|
5,00%
|
3
|
3
|
0
|
0
|
|
2,50%
|
5
|
5
|
0
|
0
|
|
1,50%
|
19
|
18
|
0
|
1
|
|
0,50%
|
582
|
480
|
86
|
16
|
|
RETAIL
|
0,5%
|
11
|
11
|
0
|
0
|
|
0,10%
|
18
|
17
|
1
|
0
|
|
0,08%
|
25
|
23
|
2
|
0
|
|
0,06%
|
50
|
47
|
3
|
0
|
|
0,04%
|
125
|
117
|
8
|
0
|
|
0,02%
|
626
|
579
|
47
|
0
|
|
0,01%
|
2 699
|
2 248
|
449
|
2
|
|
ACCIDENTS
|
90,00%
|
10
|
9
|
0
|
1
|
|
70,00%
|
16
|
15
|
0
|
1
|
|
50,00%
|
69
|
68
|
0
|
1
|
|
40,00%
|
219
|
217
|
0
|
2
|
|
30,00%
|
3 482
|
3 438
|
39
|
5
|
TAB . 4.5 -- Tableau comparatif des étapes constituant
PRINCE pour les bases éparses.
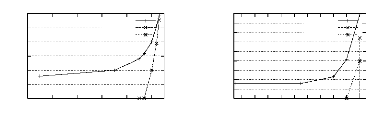
0.55
0.45
0.35
0.25
Minsup (en %)
T40I10D100K
512
étape 1
étape 2
étape 3
64
32
16
8
4
2
1
0.15 0.05 9.5 8.5 7.5 6.5 5.5 4.5 3.5 2.5 1.5 0.5
Minsup (en %)
Temps d'execution (en seconde)
Temps d'execution (en seconde)
T10I4D100K
étape 1
étape 2
étape 3
64
32
16
8
4
2
1
256
128
Temps d'execution (en seconde)
4096
1024
256
64
16
4
1
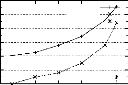
0.1
0.08
0.06
Retail
étape 1
étape 2
étape 3
0.04
0.02
0
Minsup (en %)
Temps d'execution (en seconde)
4096
1024
256
64
16
4
1
90
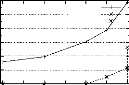
80
70
Accidents
60
étape 1
étape 2
étape 3
50
40
30
Minsup (en %)
FIG . 4.9 -- Temps d'exécution des étapes
constituant PRINCE pour les bases éparses
4.5.2 Bases "pire des cas"
Lors de ces expérimentations, nous avons utilisé
une valeur de minconf égale a 0. Pour toutes ces expérimentation,
la valeur de minsup est fixée a 1. Nous avons testé 26 bases
"pire des cas" représentant la variation de la valeur de n de 1
a 26.
Etant donné que ces bases représentent le pire
des cas, tout itemset candidat est un générateur minimal
fréquent et est égal a sa fermeture. Ainsi, l'algorithme PRINCE
n'exécute pas sa deuxième étape, cad celle relative a la
construction du treillis des générateurs minimaux. La
première étape est la plus cofiteuse étant donné le
nombre, égal a 2', de candidats générés a partir de
chaque base "pire des cas". La troisième étape est moins
cofiteuse que la première étape. Cependant, a partir d'une valeur
de n supérieure ou égale A 24, les temps
d'exécution de cette étape commencent a prendre de l'importance.
Ceci peut être expliqué par le fait que les accès, aux
informations nécessaires a l'exécution de cette étape,
s'exécutent dans l'espace d'échange et non plus en mémoire
centrale. Ainsi, ces accès deviennent de moins en moins rapides. En
effet, l'exécution des bases "pire des cas" est exigeante en espace
mémoire et sature rapidement la mémoire centrale bien que nous
minimisons la redondance en utilisant un seul trie au lieu de plusieurs. Ceci
explique l'arrêt de l'exécution de l'algorithme pour
n=26. Les temps d'exécution des différentes
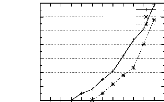
Temps d'execution (en seconde)
16384
4096
1024
256
64
16
4
1
étape 1
étape 2
étape 3
15 16 17 18 19 20 21 22 23 24 25
n
FIG . 4.10 -- Temps d'exécution des étapes
constituant PRINCE pour les bases "pire des cas"
étapes de l'algorithme PRINCE sur les bases "pire des
cas" sont présentés par la figure 4.10 et le tableau 4.6. Dans ce
dernier, "/" signifie que l'exécution n'a pas pu arriver a terme.
4.6 Performances de PRINCE vs. CLOSE, A-CLOSE et
TITANIC
Dans cette section, nous allons comparer les performances de
notre algorithme PRINCE a respectivement celles des algorithmes CLOSE, A-CLOSE
et TITANIC.
4.6.1 Bases benchmark
Les expérimentations seront divisées en deux
parties : G Expérimentations sur des bases denses ;
Expérimentations sur des bases éparses.
4.6.1.1 Experimentations sur les bases denses
Les temps d'exécution de l'algorithme PRINCE
comparés respectivement aux algorithmes CLOSE, A-CLOSE et TITANIC sur
les bases denses sont présentés par la figure 4.11 et le tableau
4.7. Dans ce dernier, les trois dernières colonnes indiquent le facteur
multiplicatif des temps d'exécution de CLOSE, A-CLOSE et TITANIC par
rapport a l'algorithme PRINCE. "/" signifie que l'exécution n'a pas pu
arriver a terme et que le ratio correspondant ne peut être
calculé.
|
n
|
Temps d,exécution total
|
1i`ere étape
|
2i`eme étape
|
3i`eme étape
|
|
15
|
1
|
1
|
0
|
0
|
|
16
|
1
|
1
|
0
|
0
|
|
17
|
1
|
1
|
0
|
0
|
|
18
|
2
|
2
|
0
|
0
|
|
19
|
4
|
3
|
0
|
1
|
|
20
|
10
|
8
|
0
|
2
|
|
21
|
23
|
18
|
0
|
5
|
|
22
|
96
|
84
|
0
|
12
|
|
23
|
429
|
403
|
0
|
26
|
|
24
|
1 525
|
1 259
|
0
|
266
|
|
25
|
16 791
|
13 634
|
0
|
3 157
|
|
26
|
/
|
/
|
/
|
/
|
TAB . 4.6 -- Tableau comparatif des étapes constituant
PRINCE pour les bases 11pire des cas11.
- PUMSB : pour cette base, les performances de PRINCE sont
meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les valeurs de
minsup. Les performances de CLOSE et A-CLOSE se dégradent
considérablement étant donné qu'ils effectuent des
intersections sur un grand nombre de transactions de taille
élevée. Le mécanisme de comptage par inférence
adopté par TITANIC s'avère plus efficace que le calcul des
intersections adopté par CLOSE et A-CLOSE. Ceci peut être
expliqué par le nombre réduit d'items fréquents a prendre
en considération lors du calcul de la fermeture d'un
générateur minimal fréquent. En effet, pour minsup = 75%,
seulement 27 items parmi 7 117 possibles sont fréquents et la taille
maximale d'un générateur minimal fréquent est égale
a 12 items. Les performances de PRINCE peuvent être expliquées par
le fait que les traitements = effectuer pour un générateur
minimal fréquent sont beaucoup moins coUteux que ceux effectués
pour les trois autres algorithmes. D'autant plus, les fonctions de gestion des
classes d'équivalence permettent a PRINCE d'éviter un calcul
redondant des fermetures tel que c'est le cas pour A-CLOSE, CLOSE et TITANIC.
En effet, pour une valeur de minsup égale a 75%, le nombre de
générateurs minimaux fréquents (égal a 248406) est
presque égal = 2,46 fois le nombre d'itemsets fermés
fréquents (égal a 101 083).
la base PUMSB, est caracterisee par un grand nombre de
transactions de taille elevee. Ces caracteristiques compliquent la tache de
CLOSE et A-CLOSE qui effectuent des operations coUteuses d'intersection. PRINCE
et TITANIC evitent ces calculs coUteux avec un avantage pour PRINCE. En effet,
PRINCE est avantage par un coUt reduit des comparaisons effectuees pour un
generateur minimal frequent compare aux tentatives d'extension executees pour
un generateur minimal frequent dans le cas de TITANIC. Il est a noter que pour
une valeur de minsup = 50%, l'execution de TITANIC n'a pu se terminer pour
manque d'espace memoire. Dans cette base, et malgre qu'il n'y a aucun calcul
redondant des fermetures pour les trois algorithmes CLOSE, A-CLOSE et TITANIC
(le nombre de generateurs minimaux frequents est egal a celui des itemsets
fermes frequents), les performances de notre algorithme restent les
meilleures.
Vu le nombre de transactions et la taille moyenne des
transactions qui caracterisent les bases PUMSB et CONNECT, le calcul des
supports des candidats constituent une operation coUteuse pour les algorithmes
testes. Ainsi, la representation compacte de la base adoptee dans PRINCE et
l'utilisation d'un fichier binaire dans le cas des trois autres algorithmes
constituent des tentatives de reduction du coUt de cette operation.
- - CHESS : pour cette base, les performances de PRINCE sont
largement meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les
valeurs de minsup. Comme pour les deux premieres bases, notre algorithme est
avantage par un coUt reduit des traitements a executer pour chaque generateur
minimal frequent compare aux trois autres algorithmes. Le mecanisme de comptage
par inference adopte par TITANIC s'avere plus efficace que le calcul des
intersections adopte par les algorithmes CLOSE et A-CLOSE. Cependant, cette
efficacite tend a diminuer avec la baisse de la valeur de minsup. En effet,
pour calculer les itemsets fermes frequents, TITANIC essaie d'etendre tout
generateur minimal frequent par les items frequents adequats. Ceci necessite
des recherches de supports dont le nombre augmente avec l'augmentation du
nombre d'items frequents, chaque fois que la valeur de minsup diminue.
- MUSHROOM : dans le cas de la base MUSHROOM, PRINCE est
encore une fois meilleur que CLOSE, A-CLOSE et TITANIC. Pour cette base,
l'etape de calcul du support ne pese pas lourd sur les performances des quatre
algorithmes (vu le nombre reduit de transactions dans la base MUSHROOM ainsi
que la taille moyenne reduite des transactions). Cependant, les operations
relatives a la construction de l'ordre partiel dans le cas de PRINCE et au
calcul des fermetures dans le cas des trois autres algorithmes sont les
operations
les plus coUteuses. Les performances de notre algorithme
restent meilleures etant donne l'importance du role joue par les fonctions de
gestion des classes d'equivalence. En effet, pour une valeur de minsup egale a
0,1%, le nombre de generateurs minimaux frequents (egal a 360 166) est presque
egal a 2,20 fois le nombre d'itemsets fermes frequents (egal a 164117). De
meme, l'utilisation d'une liste prohibee au niveau de chaque classe
d'equivalence permet de reduire considerablement le nombre de comparaisons et
donc d'ameliorer les performances de notre algorithme. Ainsi, bien que CLOSE et
A-CLOSE beneficient d'un nombre reduit de transactions ainsi qu'une taille
moyenne des transactions relativement petite sur lesquelles ils executent des
intersections, ces deux algorithmes sont handicapes par un calcul redondant des
fermetures. De son cote, TITANIC fait mieux que CLOSE et A-CLOSE pour des
supports compris entre 20% et 2% alors que la tendance est largement inversee
en faveur de CLOSE et A-CLOSE pour des supports au dessous de 2%. Ceci peut
etre explique par le fait que TITANIC effectue beaucoup de recherches des items
adequats. Le nombre de ces recherches augmente considerablement, avec la baisse
des valeurs de minsup, etant donne que le nombre d'items frequents devient
eleve. En effet, pour minsup : 0,1%, 116 items sont frequents parmi 119
possibles et la taille maximale d'un generateur minimal frequent est egale a 10
items seulement.
L'algorithme PRINCE s'avere performant sur les bases denses et
pour toutes les valeurs de minsup. La difference entre les performances de
PRINCE et celles de CLOSE et A-CLOSE atteint son maximum pour la base PUMSB. En
effet, PRINCE est environ 160 (resp. 403) fois plus rapide que CLOSE (resp.
A-CLOSE) pour un support de 85%. De meme, PRINCE est environ 538 fois plus
rapide que TITANIC pour la base MUSHROOM et pour un support egal a 0,01%. Pour
ces bases denses, PRINCE est en moyenne 42 (resp. 89 et 41) fois plus rapide
que CLOSE (resp. A-CLOSE et TITANIC).
4.6.1.2 Experimentations sur les bases eparses
Les temps d'execution de l'algorithme PRINCE compares
respectivement aux algorithmes CLOSE, A-CLOSE et TITANIC sur les bases eparses
sont presentes par la figure 4.12 et le tableau 4.8. Dans ce dernier, les trois
dernieres colonnes indiquent le facteur multiplicatif des temps d'execution de
CLOSE, A-CLOSE et TITANIC par rapport a l'algorithme PRINCE. "/" signifie que
l'execution n'a pas pu arriver a terme et que le ratio correspondant ne peut
etre calcule.
|
Base
|
rninsup
|
PRINCE
(en sec)
|
CLOSE (en sec)
|
A -CLOSE (en sec)
|
TITANIC (en sec)
|
i-
|
Ai,RCILN°csEE
|
T,IRTIANNciEc
|
|
PRINCEi°NscEE
|
|
|
|
PUMSB
|
95,00%
|
|
3
|
|
74
|
|
172
|
|
12
|
24,67
|
57,33
|
4,00
|
|
90,00%
|
|
7
|
|
679
|
1
|
914
|
|
36
|
97,00
|
273,43
|
5,14
|
|
85,00%
|
|
27
|
4
|
332
|
10
|
875
|
|
192
|
160,44
|
402,78
|
7,11
|
|
80,00%
|
|
416
|
19
|
848
|
47
|
167
|
1
|
233
|
47,71
|
113,38
|
2,96
|
|
75,00%
|
1
|
641
|
65
|
690
|
152
|
050
|
4
|
563
|
40,03
|
92,66
|
2,78
|
|
CONNECT
|
90,00%
|
|
8
|
|
853
|
1
|
652
|
|
23
|
106,62
|
206,50
|
2,87
|
|
80,00%
|
|
25
|
3
|
428
|
5
|
771
|
|
135
|
137,12
|
230,84
|
5,40
|
|
70,00%
|
|
66
|
7
|
358
|
12
|
028
|
|
452
|
111,48
|
182,24
|
6,85
|
|
60,00%
|
|
332
|
13
|
024
|
20
|
747
|
1
|
205
|
39,23
|
62,49
|
3,63
|
|
50,00%
|
|
847
|
22
|
164
|
35
|
903
|
|
/
|
26,17
|
42,39
|
/
|
|
CHESS
|
90,00%
|
|
1
|
|
6
|
|
15
|
|
1
|
6,00
|
15,00
|
1,00
|
|
80,00%
|
|
1
|
|
49
|
|
122
|
|
3
|
49,00
|
122,00
|
3,00
|
|
70,00%
|
|
3
|
|
217
|
|
481
|
|
25
|
72,33
|
160,33
|
8,33
|
|
60,00%
|
|
39
|
|
784
|
1
|
896
|
|
233
|
20,10
|
48,61
|
5,97
|
|
50,00%
|
|
197
|
2
|
560
|
5
|
451
|
1
|
520
|
12,99
|
27,67
|
7,71
|
|
45,00%
|
|
435
|
4
|
550
|
9
|
719
|
4
|
237
|
10,46
|
22,34
|
9,74
|
|
MUSHROOM
|
20,00%
|
|
1
|
|
14
|
|
28
|
|
2
|
14,00
|
28,00
|
2,00
|
|
10,00%
|
|
1
|
|
32
|
|
69
|
|
5
|
32,00
|
69,00
|
5,00
|
|
5,00%
|
|
3
|
|
59
|
|
121
|
|
21
|
19,67
|
40,33
|
7,00
|
|
3,00%
|
|
4
|
|
83
|
|
163
|
|
46
|
20,75
|
40,75
|
11,50
|
|
2,00%
|
|
7
|
|
98
|
|
197
|
|
81
|
14,00
|
28,14
|
11,57
|
|
1,00%
|
|
13
|
|
123
|
|
250
|
|
180
|
9,46
|
19,23
|
13,85
|
|
0,80%
|
|
17
|
|
132
|
|
270
|
|
246
|
7,76
|
15,88
|
14,47
|
|
0,30%
|
|
33
|
|
154
|
|
322
|
3
|
127
|
4,67
|
9,76
|
94,76
|
|
0,20%
|
|
40
|
|
159
|
|
336
|
10
|
518
|
3,97
|
8,40
|
262,95
|
|
0,10%
|
|
50
|
|
168
|
|
352
|
26
|
877
|
3,36
|
7,04
|
537,54
|
TAB . 4.7 - Tableau comparatif des resultats experimentaux de
PRINCE vs. A-CLOSE, CLOSE et TITANIC pour les bases denses.

Temp d'execution (en seconde)
65536
16384
4096
1024
256
64
16
4
90
80
Connect
70
Prince
Close A-Close Titanic
60
50
Temps d'execution (en seconde)
262144
65536
16384
4096
1024
256
64
16
4
1
95
90
Pumsb
85
Prince
Close A-Close Titanic
80
75
65536
16384
4096
1024
256
64
16
4
1
Temps d'execution (en seconde)
m insup (en %)
16384
4096
1024
256
64
16
4
1
Temps d'execution (en seconde)
Chess

Prince
Close A-Close Titanic
90 80 70 60 50 40
m insup (en %)
m insup (en %)
Mushroom

Prince
Close A-Close Titanic
20 18 16 14 12 10 8 6 4 2 0
m insup (en %)
FIG . 4.11 -- Les performances de PRINCE vs. CLOSE, A-CLOSE et
TITANIC pour les bases denses
PRINCE fait mieux que cet algorithme pour des valeurs de
minsup supérieures ou égales a 0,03%. Alors que c'est l'inverse
pour des supports inférieurs a 0,03%. Ceci peut être
expliqué par le fait que PRINCE est pénalisé par le coiit
de la construction de l'ordre pour de tres basses valeurs de minsup. Cependant,
CLOSE est avantagé par une taille moyenne des transactions relativement
faible (10 items). Notons que pour des valeurs de minsup supérieures ou
égales a 0,5%, chaque générateur minimal fréquent
est un fermé. Ainsi, PRINCE ne nécessite pas l'exécution
de la procédure GEN-ORDRE étant donné que l'ordre est
déjà construit a la fin de la premiere étape. De son
coté, A-CLOSE n'effectue aucun calcul de fermeture. Ainsi, A-CLOSE prend
le dessus sur CLOSE. Cependant, comparé a PRINCE pour les mêmes
valeurs de support (supérieures ou égales a 0,5%), A-CLOSE se
voit moins rapide en raison du balayage supplémentaire de l'ensemble des
générateurs minimaux fréquents de taille (k-1)
effectué pour chaque candidat g de taille k. Ce
balayage permet de comparer le support de g a celui de ses
sous-ensembles de taille (k-1) afin de savoir si g est
minimal ou non. Au fur et a mesure que la valeur de minsup diminue, les
performances de TITANIC se dégradent considérablement. En effet,
le nombre d'items fréquents, a considérer dans le calcul de la
fermeture d'un générateur minimal fréquent, croit
énormément suite a la baisse des valeurs de minsup. Ainsi, pour
minsup=0,02%, 859
items sont frequents parmi 1 000 possibles et la taille maximale
d'un generateur minimal frequent est egale a 10 items seulement.
- T40I10D1OOK : les performances de PRINCE dans cette base
sont largement meilleures que celles de CLOSE, A-CLOSE et TITANIC quelle que
soit la valeur de minsup. Pour les valeurs de minsup superieures ou egales a
1,5%, le scenario de la base T10I4D100K, pour des valeurs de minsup superieures
ou egales a 0,5%, semble se repeter. En effet, pour ces valeurs, chaque
generateur minimal frequent est aussi un ferme. Pour des supports inferieurs a
1,5%, A-CLOSE est oblige de calculer les fermetures. Ainsi, CLOSE et A-CLOSE
sont handicapes par une taille moyenne elevee des transactions (40 items)
sachant que CLOSE prend le dessus sur A-CLOSE. De même, les performances
de TITANIC se degradent d'une manière considerable pour les mêmes
raisons evoquees auparavant. Le coUt des comparaisons, dans le cas de PRINCE,
etant nettement plus reduit que le coUt du calcul des intersections (resp. des
tentatives d'extension) pour calculer la fermeture d'un generateur minimal
frequent dans le cas de CLOSE et A-CLOSE (resp. TITANIC) explique l'ecart dans
les performances entre PRINCE et les trois autres algorithmes.
- - RETAIL : pour cette base, notre algorithme realise des
temps d'execution beaucoup moins importants que ceux realises par CLOSE,
A-CLOSE et TITANIC. Pour des valeurs de minsup superieures a 0,08%, les temps
d'execution de PRINCE, CLOSE et A-CLOSE restent comparables avec un avantage
pour PRINCE. Pour des valeurs de minsup superieures a 0,06%, les performances
de PRINCE et A-CLOSE restent comparables avec un avantage pour PRINCE.
Toutefois, les performances de CLOSE se degradent considerablement. Pour des
valeurs de supports inferieures a 0,06%, les performances de A-CLOSE se
degradent aussi d'une manière significative. Ces performances peuvent
être expliquees par l'influence enorme du nombre eleve d'items dans
RETAIL. En effet, CLOSE est handicape par un nombre enorme de candidats pour
lesquels il est oblige de calculer la fermeture alors qu'un grand nombre
d'entre eux s'avèrera non frequent. Le nombre de candidats affecte aussi
les performances de A-CLOSE a cause des balayages supplementaires ainsi que le
coUt du calcul des fermetures. De son cote, TITANIC est considerablement
alourdi par un grand nombre d'items frequents a considerer lors du calcul de la
fermeture d'un generateur minimal frequent (pour minsup = 0,04%, 4 463 items
sont frequents et la taille maximale d'un generateur minimal frequent est egale
a 6 items seulement). L'execution de TITANIC, pour des supports inferieurs a
0,04%, s'arrête pour manque d'espace memoire. PRINCE fait mieux que les
trois autres algorithmes etant donne que les traitements relatifs a chaque
generateur minimal sont nettement moins coUteux.
- ACCIDENTS : dans cette base, les performances de PRINCE sont
meilleures que celles de CLOSE, A-CLOSE et TITANIC pour toutes les valeurs de
minsup. Pour des valeurs de minsup superieures ou egales a 40%, chaque
generateur minimal frequent est un ferme. Ainsi, le meme scenario, que dans les
cas des bases T10I4D100K et T40D10I100K pour des supports respectivement
superieurs ou egaux a 0,5% et 1,5%, s'est repete. CLOSE est enormement
desavantage par un nombre eleve de transactions que contient ACCIDENTS ainsi
qu'une taille moyenne des transactions relativement elevee. Ceci induit des
coits enormes pour le calcul des fermetures. Pour des supports inferieurs a
40%, PRINCE doit executer sa deuxieme etape (cad la procedure GEN-ORDRE) pour
construire l'ordre partiel. Les performances de A-CLOSE se degradent d'une
maniere considerable etant donne qu'il est oblige de calculer les fermetures
sur un nombre eleve de transactions. Le mecanisme de comptage par inference
adopte par TITANIC s'avere plus efficace que le calcul des intersections adopte
par CLOSE et A-CLOSE. Ceci peut etre explique par le nombre reduit d'items
frequents a prendre en consideration lors du calcul de la fermeture d'un
generateur minimal frequent. En effet, seuls 32 items parmi 468 sont frequents
pour minsup egal a 30% et la taille maximale d'un generateur minimal frequent
est egale a 12 items. Pour la base ACCIDENTS et pour toutes les valeurs de
minsup, l'operation consistant en le calcul des supports des candidats pese
enormement lourd sur les quatre algorithmes (il y a un nombre eleve de
transactions de taille moyenne relativement elevee). Ainsi, dans le cas de
l'algorithme PRINCE, la representation compacte de la base presente une
solution importante pour faire face au coit de cette operation. Il en est de
meme pour la raison de l'utilisation d'un fichier binaire en entree des trois
autres algorithmes.
L'algorithme PRINCE s'avere aussi performant sur les bases
eparses et pour toutes les valeurs de minsup. La difference entre les
performances de PRINCE et celles de CLOSE et TITANIC atteint son maximum pour
la base RETAIL. En effet, PRINCE est environ 115 (resp. 261) fois plus rapide
que CLOSE (resp. TITANIC) pour un support de 0,04%. De meme, PRINCE est environ
57 fois plus rapide que A-CLOSE pour la base ACCIDENTS et pour une valeur de
minsup egale a 30%. Pour ces bases eparses, PRINCE est en moyenne 31 (resp. 13
et 32) fois plus rapide que CLOSE (resp. A-CLOSE et TITANIC).
4.6.2 Bases !!pire des cas!!
Pour toutes ces experimentation, la valeur de minsup est fixee
a 1. Nous avons teste 26 bases "pire des cas" representant la variation de la
valeur de n de 1 a 26. Etant donne que ces bases representent le pire
des cas, tout itemset candidat est un generateur minimal
Temps d'execution (en seconde)
Temps d'execution (en seconde)

T40I10D100K
262144
65536
16384
4096
1024
256
64
16
4
1
Prince
Close A-Close Titanic
T10I4D100K

Prince Close A-Close Titanic
2048
1024
512
256
128
64
32
16
8
4
2
0.55 0.45 0.35 0.25
0.15 0.05 9.5 8.5 7.5 6.5 5.5 4.5 3.5 2.5 1.5
m insup (en %)
0.5
m insup (en %)
Temps d'execution (en seconde)
262144
65536
16384
4096
1024
256
64
16

0.1
0.08
0.06
Retail
Prince Close A-Close Titanic
0.04
0.02
0
Temps d'execution (en seconde)
262144
65536
16384
4096
1024
256
64
16
4
90

80
70
Accidents
60
Prince
Close A-Close Titanic
50
40
30
m insup (en %) m insup (en %)
FIG . 4.12 -- Les performances de PRINCE vs. CLOSE, A-CLOSE et
TITANIC pour les bases éparses
fréquent et est égal a sa fermeture.
Les temps d'exécution des quatre algorithmes ne
commencent a être distinguables qu'à partir d'une valeur de
n égale a 15. Pour les bases "pire des cas", les performances de
PRINCE restent meilleures que celles de CLOSE, A-CLOSE et TITANIC. Chaque
générateur minimal fréquent est aussi un fermé.
Ainsi, PRINCE n'exécute pas sa deuxieme étape, le treillis des
générateurs minimaux étant construit des la fin de sa
premiere étape. De son coté, A-CLOSE ne calcule pas les
fermetures. D'oft, ses performances sont meilleures que celles de CLOSE et
celles de TITANIC. Notons que dans ce type de bases, chaque candidat est un
générateur minimal fréquent. Ainsi, pour chaque
itemset g de taille k (qui est un générateur
minimal fréquent), A-CLOSE et TITANIC effectuent un balayage des
sous-ensembles de g de taille (k-1). Dans le cas de A-CLOSE,
ce balayage permet de vérifier que le candidat g a un support
différent de celui de ces sous-ensembles en question pour le qualifier
de générateur minimal fréquent. Dans le cas de TITANIC, ce
balayage permet d'optimiser le calcul de la fermeture de g en
collectant les items appartenant aux fermetures des sous-ensembles en question.
De plus, TITANIC essaie l'étendre l'itemset résultat de ce
balayage par les items adéquats. De son coté, CLOSE est aussi
contraint a calculer la fermeture de tout itemset fréquent, ce dernier
étant un générateur minimal
frequent. Il est important de noter que les calculs de
fermetures effectues par CLOSE et TITANIC s'avereront sans utilite car tout
generateur minimal est egal a sa fermeture. L'execution de ces deux algorithmes
n'ont pu se terminer pour une valeur de n egale a 24, en raison du
manque d'espace memoire. Pour la meme raison, l'execution de A-CLOSE n'a pu se
terminer pour une valeur de n egale a 25. L'execution de notre
algorithme prend aussi fin, pour n26. La figure 4.13 et le tableau 4.9
donnent le comportement des algorithmes suivant la variation de la valeur
de n. Dans le tableau 4.9, les trois dernieres colonnes indiquent le
facteur multiplicatif des temps d'execution de CLOSE, A-CLOSE et TITANIC par
rapport a l'algorithme PRINCE. "/" signifie que l'execution n'a pas pu arriver
a terme et que le ratio correspondant ne peut etre calcule.
Ce test de mise a l'echelle montre aussi l'interêt de
l'utilisation d'un seul trie pour stocker les informations relatives a tous les
generateurs minimaux (cas de PRINCE) comparee a l'utilisation de plusieurs
tries dans le cas des trois autres algorithmes. En effet, pour CLOSE, A-CLOSE
et TITANIC, un trie est utilise pour stocker les informations relatives a
chaque ensemble de generateurs minimaux d'une taille k donnee. Ceci
rend eleve le nombre d'informations redondantes stockees dans ces tries et
augmente ainsi l'espace memoire necessaire.
L'algorithme PRINCE reste meilleur que les algorithmes CLOSE,
A-CLOSE et TITANIC sur les bases "pire des cas". La difference entre les
performances de PRINCE et celles de CLOSE (resp. A-CLOSE et TITANIC) est
maximale pour n21 (resp. 19 et 23). En effet, pour ces valeurs de
n, PRINCE est environ 29 (resp. 4 et 10) fois plus rapide que CLOSE (resp.
A-CLOSE et TITANIC). Pour ces bases "pire des cas", PRINCE est en moyenne 16
(resp. 3 et 4) fois plus rapide que CLOSE (resp. A-CLOSE et TITANIC).
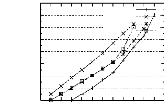
Temps d'execution (en seconde)
65536
16384
4096
1024
256
64
16
4
1
Prince
Close A-Close Titanic
15 16 17 18 19 20 21 22 23 24 25
n
4.7 Conclusion
Dans ce chapitre, nous avons présenté une
étude expérimentale sur l'algorithme PRINCE, que nous avons
proposé, pour l'extraction des itemsets fermés fréquents,
leurs générateurs minimaux associés ainsi que les regles
génériques informatives valides. Les expérimentations, que
nous avons menées, concernent l'étude de quelques optimisations
apportées a l'algorithme PRINCE ainsi qu'une analyse de ses
caractéristiques. Ensuite, nous avons effectué différents
tests, sur des bases benchmark et sur des bases "pire des cas", pour
évaluer les performances de l'algorithme PRINCE comparées a
celles des algorithmes CLOSE, A-CLOSE et TITANIC. Ces expérimentations
ont montré que PRINCE est plus performant que les algorithmes
d'exploration nivelée existants dans la littérature pour tous les
types de bases utilisées.
|
Base
|
rninsup
|
PRINCE
(en sec)
|
CL0SE (en sec)
|
A - C L 0 S E (en sec)
|
TITANIC (en sec)
|
i-
|
Ai,RCILN°csEE
|
T,IRTIANNciEc
|
|
PRINCEj'aNscEE
|
|
|
|
T10I4D100K
|
0,50%
|
|
3
|
|
17
|
|
9
|
|
7
|
5,67
|
3,00
|
2,33
|
|
0,20%
|
|
4
|
|
26
|
|
40
|
|
58
|
6,50
|
10,00
|
14,50
|
|
0,10%
|
|
8
|
|
34
|
|
57
|
|
136
|
4,25
|
7,12
|
17,00
|
|
0,08%
|
|
10
|
|
37
|
|
62
|
|
174
|
3,70
|
6,20
|
17,40
|
|
0,05%
|
|
20
|
|
49
|
|
71
|
|
247
|
2,45
|
3,55
|
12,35
|
|
0,03%
|
|
50
|
|
66
|
|
87
|
|
387
|
1,32
|
1,74
|
7,74
|
|
0,02%
|
|
105
|
|
93
|
|
108
|
1
|
316
|
0,88
|
1,03
|
12,53
|
|
T40I10D100K
|
10,00%
|
|
3
|
|
44
|
|
23
|
|
20
|
14,67
|
7,67
|
6,67
|
|
5,00%
|
|
3
|
|
140
|
|
43
|
|
21
|
46,67
|
14,33
|
7,00
|
|
2,50%
|
|
5
|
|
238
|
|
67
|
|
26
|
47,60
|
13,40
|
5,20
|
|
1,50%
|
|
19
|
|
366
|
|
108
|
|
66
|
19,26
|
5,68
|
3,47
|
|
0,50%
|
|
582
|
5
|
420
|
11
|
564
|
117
|
636
|
9,31
|
19,87
|
202,12
|
|
RETAIL
|
0,10%
|
|
18
|
|
37
|
|
33
|
|
158
|
2,05
|
1,83
|
8,78
|
|
0,08%
|
|
25
|
|
52
|
|
43
|
|
415
|
2,08
|
1,72
|
16,60
|
|
0,06%
|
|
50
|
2
|
185
|
|
63
|
3
|
089
|
43,70
|
1,26
|
61,78
|
|
0,04%
|
|
125
|
14
|
358
|
1
|
833
|
32
|
663
|
114,86
|
14,66
|
261,30
|
|
0,02%
|
|
626
|
53
|
208
|
18
|
269
|
|
/
|
85,00
|
29,18
|
/
|
|
0,01%
|
2
|
699
|
159
|
217
|
52
|
162
|
|
/
|
58,99
|
19,33
|
/
|
|
ACCIDENTS
|
90,00%
|
|
10
|
|
79
|
|
50
|
|
25
|
7,90
|
5,00
|
2,50
|
|
70,00%
|
|
16
|
|
440
|
|
206
|
|
63
|
27,50
|
12,87
|
3,94
|
|
50,00%
|
|
69
|
4
|
918
|
1
|
839
|
|
381
|
71,27
|
26,65
|
5,52
|
|
40,00%
|
|
219
|
17
|
528
|
6
|
253
|
2
|
120
|
80,04
|
28,55
|
9,68
|
|
30,00%
|
3
|
482
|
170
|
540
|
199
|
980
|
9
|
530
|
48,98
|
57,43
|
2,74
|
TAB . 4.8 - Tableau comparatif des resultats experimentaux de
PRINCE vs. A-CLOSE, CLOSE et TITANIC pour les bases eparses.
|
n
|
PRINCE
(en sec)
|
CLOSE (en sec)
|
A-CLOSE (en sec)
|
TITANIC (en sec)
|
CLOSE
|
ACLOSE
|
TITANIC
|
|
PRINCE
|
PRINCE
|
PRINCE
|
|
15
|
1
|
2
|
|
1
|
1
|
2,00
|
1,00
|
1,00
|
|
16
|
1
|
5
|
|
2
|
2
|
5,00
|
2,00
|
2,00
|
|
17
|
1
|
13
|
|
4
|
4
|
13,00
|
4,00
|
4,00
|
|
18
|
2
|
32
|
|
8
|
9
|
16,00
|
4,00
|
4,50
|
|
19
|
4
|
81
|
|
17
|
17
|
20,25
|
4,25
|
4,25
|
|
20
|
10
|
217
|
|
36
|
37
|
21,70
|
3,60
|
3,70
|
|
21
|
23
|
670
|
|
77
|
80
|
29,13
|
3,35
|
3,48
|
|
22
|
96
|
2 058
|
|
200
|
353
|
21,44
|
2,08
|
3,68
|
|
23
|
429
|
5 932
|
|
890
|
4 129
|
13,83
|
2,10
|
9,62
|
|
24
|
1 525
|
/
|
3
|
519
|
/
|
/
|
2,31
|
/
|
|
25
|
16 791
|
/
|
|
/
|
/
|
/
|
/
|
/
|
|
26
|
/
|
/
|
|
/
|
/
|
/
|
/
|
/
|
TAB . 4.9 -- Tableau comparatif des resultats experimentaux de
PRINCE vs. A-CLOSE, CLOSE et TITANIC pour les bases "pire des cas".
Conclusion générale
La fouille de donnees est un domaine qui est apparu suite a un
besoin incessant exprime par les entreprises. Ce besoin consiste en l'analyse
des flux de donnees qui s'accumulent quotidiennement dans leurs bases de
donnees. Partant du fait que l'analyse de ces donnees est une solution cle pour
toute entreprise voulant tirer profit des masses d'informations stockees, la
fouille des donnees s'est vite integree dans differents domaines [42]. La
fouille de donnees englobe plusieurs techniques, dont l'extraction des regles
d'association. Ainsi, l'approche basee sur l'extraction des itemsets fermes
frequents [48], issue de l'analyse formelle de concepts [66], presentait une
promesse claire de reduire, sans perte d'information, la liste de toutes les
regles d'association extraites d'un contexte. Ceci donnait la possibilite de
presenter un ensemble minimal de regles a l'utilisateur afin de lui permettre
de mieux les visualiser et les exploiter. Une etude critique nous a permis de
constater que les algorithmes dediees a cette approche ont failli a cette
promesse. En effet, ils ne font qu'extraire les itemsets fermes frequents et au
plus leurs generateurs minimaux associes sans se soucier de la relation d'ordre
partiel.
Afin de satisfaire la promesse apportee par l'approche basee
sur l'extraction des itemsets fermes frequents, nous avons introduit un nouvel
algorithme, appele PRINCE, permettant d'extraire les composantes suivantes :
1. Les itemsets fermes frequents ;
2. Les generateurs minimaux associes aux itemsets fermes
frequents ;
3. La relation d'ordre sous-jacente.
La principale originalite de l'algorithme introduit est qu'il
construit une structure partiellement ordonnee, appelee treillis des
générateurs minimaux. Cette structure maintient la relation
d'ordre partiel entre les generateurs minimaux frequents et non plus entre les
itemsets fermes frequents. Une fois cette structure construite, la generation
des bases generiques de regles d'association devient immediate. En effet, un
parcours ascendant permet de deriver les regles generiques sans avoir a
calculer les fermetures. L'etude de la
complexité théorique de l'algorithme PRINCE nous
a montré que sa complexité au pire des cas est linéaire en
fonction du nombre d'itemsets fermés fréquents 2'. Cependant,
cette complexité théorique reste de même ordre de grandeur
que celle des algorithmes dédiés a l'extraction des itemsets
fermés fréquents. L'étude expérimentale, que nous
avons menée, a porté sur deux parties. La première partie
a consisté a tester l'effet des optimisations apportées a
l'algorithme PRINCE et a analyser ses caractéristiques. La
deuxième partie s'est intéressée a comparer les
performances de notre algorithme comparées a celles des algorithmes
CLOSE, A-CLOSE et TITANIC. Cette deuxième partie des
expérimentations a montré que l'algorithme PRINCE est plus
performant que les algorithmes CLOSE, A-CLOSE et TITANIC sur les bases
benchmark et les bases "pire des cas". En effet, PRINCE est en moyenne 33
(resp. 45 et 32) fois plus rapide que CLOSE (resp. A-CLOSE et TITANIC) et la
différence atteint 160 (resp. 403 et 538) fois.
Bien que les résultats obtenus sont encourageants,
plusieurs perspectives de travaux futurs peuvent être envisagées
pour l'amélioration des performances de l'algorithme PRINCE. Ces
perspectives sont comme suit :
G L'étude de la possibilité d'intégrer la
notion d'itemsets non-dérivables fréquents [18] dans la
première étape de PRINCE, cad Détermination des
générateurs minimaux. En effet, cette notion s'applique a tout
ensemble vérifiant la propriété d'idéal d'ordre tel
que l'ensemble des générateurs minimaux dans notre cas. Elle
permet d'estimer, moyennant l'application d'un système
d'inéquations, le support minimal (lower bound) et le support
maximal (upper bound) que peut avoir un candidat c. Si ces deux
supports sont égaux, il n'y a nul besoin d'ajouter c parmi les
candidats auxquels un accès au contexte d'extraction est
nécessaire pour calculer leurs supports car le support réel
de c est égal a son support minimal (égal a son support
maximal). Ainsi, cette intégration devrait réduire le nombre de
candidats lors de l'étape, parfois cofiteuse, du calcul du support des
candidats. Il serait alors intéressant de voir si malgré le cofit
induit par l'application du système d'inéquations pour chaque
candidat, l'intégration de ces travaux permettent de réduire le
cofit du calcul du support.
Un remplacement du stockage de la bordure négative des
générateurs minimaux GBd-, utilisée
lors de la deuxième étape de PRINCE, par le stockage d'un
sous-ensemble de GBd-, appelée bordure
négative des générateurs minimaux infréquents et
notée IDFreeGBd- [39]. En effet, dans [39], l'auteur
montre que l'union de l'ensemble des générateurs minimaux
fréquents GMFK et de IDFreeGBd- est une
représentation concise de l'ensemble des itemsets fréquents. Ce
stockage présente un avantage,
a savoir de reduire l'espace de recherche lors de la recherche
d'un support dans la deuxieme etape. Cependant, il presente aussi une
contrainte, a savoir le coUt de la determination de
IDFreeGBd- [39]. L'elaboration d'une version de PRINCE
utilisant IDFreeGBd- au lieu de GBd-
parait interessante a tester.
La reduction d'avantage du nombre de regles generiques
extraites et ceci moyennant deux pistes possibles :
1. Utilisation d'autres contraintes autres que le seuil minimum
de confiance, minconf [15].
2. Restriction de l'extraction des bases generiques
informatives aux generateurs minimaux frequents formant une representation
succincte des generateurs minimaux [22]. Cette representation est de taille
inferieure a celle de l'ensemble des generateurs minimaux frequents
GMFK et permet ainsi de reduire le nombre de regles informatives. Il
serait alors interessant d'etudier les proprietes des nouvelles bases obtenues
ainsi que de trouver un systeme axiomatique permettant de retrouver toutes les
regles formant les bases generiques informatives.
Bibliographie
[1] R. Agrawal, T. Imielinski, an d A. Swami. Mining
association rules between sets of items in large databases. In Proceedings of
the ACM-SIGMOD Intl. Conference on Management of Data, Washington D. C., USA,
pages 207216, May 1993.
[2] R. Agrawal an d R. Srikant. Fast algorithms for mining
association rules. In J. B. Bocca, M. Jarke, an d C. Zaniolo, editors,
Proceedings of the 20th Intl. Conference on Very Large Databases, Santiago,
Chile, pages 478-499, June 1994.
[3] M. Barbut an d B. Monjar det. Ordre et classification.
Algèbre et Combinatoire. Hachette, Tome II, 1970.
[4] Y. Basti de. Data mining : algorithmes par niveau,
techniques d,implantation et applications. These de doctorat, Ecole
Doctorale Sciences pour l,Ingénieur de Clermont-Ferrand,
Université Blaise Pascal, France, Décembre 2000.
[5] Y. Basti de, N. Pasquier, R. Taouil, L. Lakhal, an d G.
Stumme. Mining minimal non-redundant association rules using frequent close d
itemsets. In Proceedings of the International Conference DOOD'2000,
Springer-Verlag, LNAI, volume 1861, London, UK, pages 972986, July 2000.
[6] Y. Basti de, R. Taouil, N. Pasquier, G. Stumme, an d L.
Lakhal. Mining frequent patterns with counting inference. The Sixth ACM-SIGKDD
International Conference on Knowledge Discovery and Data Mining, Boston,
Massachusetts, USA, 2(2) :6675, August 2023, 2000.
[7] S. BenYahia, C. L. Cherif, G. Mineau, an d A. Jaoua.
Découverte des regles associatives non re don dantes : application aux
corpus textuels. Revue d'Intelligence Artificielle (special issue of Intl.
Conference of Journées francophones d'Extraction et Gestion des
Connaissances (EGC'2003)), Lyon, France, 17(123) :131143, 2224 Janvier 2003.
[8] S. BenYahia, N. Doggaz, Y. Slimani, an d J. Rezgui. A
Galois connection semantics-based approach for deriving generic bases of
association rules. Revue d'Intelligence Artificielle (special issue of Intl.
Conference of Journées francophones d'Extraction et Gestion des
Connaissances (EGC'2004)), Clermont-Ferrand, France, 17(1) :131143, 2124
Janvier 2004.
[9] S. BenYahia an d E. Mephu Nguifo. Approches
d,extraction de regles d,association basées sur la
correspon dance de Galois. In J.-F. Boulicault an d B. Cremilleux, editors,
Revue
d'Ingénierie des Systêmes d'Information (ISI),
Hermês-Lavoisier, volume 9, pages 2355, 2004.
[10] S. BenYahia an d E. Mephu Nguifo. Revisiting generic
bases of association rules. In Proceedings of 6th International Conference on
Data Warehousing and Knowledge Discovery (DaWaK 2004), LNCS 3181,
Springer-Verlag, Zaragoza, Spain, pages 58-67, September 13, 2004.
[11] M. J. A. Berry an d G. S. Linoff. Data Mining Techniques :
For Marketing, Sales, and Customer Relationship Management, Second Edition.
Wiley Publishing, 2004.
[12] F. Bo don. A fast apriori implementation. In B. Goethals
an d M. J. Zaki, editors, Proceedings of the IEEE ICDM Workshop on Frequent
Itemset Mining Implementations (FIMI'03), volume 90 of CEUR Workshop
Proceedings, Melbourne, Florida, USA, November 19, 2003.
[13] F. Bo don. Surprising results of trie-base d fim
algorithms. In B. Goethals, M. J. Zaki, and R. Bayar do, editors, Proceedings
of the IEEE ICDM Workshop on Frequent Itemset Mining Implementations (FIMI'04),
volume 126 of CEUR Workshop Proceedings, Brighton, UK, November 1st 2004.
[14] F. Bo don an d L. Rányai. Trie : An alternative
data structure for data mining algorithms. Journal of Hungarian Applied
Mathematics and Computer Application, 38(7-9) :739751, October 2003.
[15] F. Bonchi an d C. Lucchese. On close d constraine d
frequent pattern mining. In Proceedings of the Fourth IEEE International
Conference on Data Mining (ICDM'04), Brighton, UK, pages 3542, November 14,
2004.
[16] J.-F. Boulicault an d B. Crémilleux. Editorial du
volume. In J.-F. Boulicault an d B. Cremilleux, editors, Revue
d'Ingénierie des Systêmes d'Information (ISI),
Hermês-Lavoisier, volume 9, pages 722, 2004.
[17] T. Brijs, G. Swinnen, K. Vanhoof, an d G. Wets. Using
association rules for product as-
sortment decisions : A case study. In Proceedings of the sixth
ACM-SIGKDD International
Conference on Knowledge Discovery and Data Mining, San Diego,
California, USA, pages
254260, August 1518 1999.
[18] T. Cal ders an d B. Goethals. Mining all non-derivable
frequent itemsets. In T. Elomaa, H. Mannila, an d H. Toivonen, editors,
Proceedings of the 6th European Conference on Principles of Data Mining and
Knowledge Discovery, PKDD 2002, LNCS, volume 2431, Springer-Verlag, Helsinki,
Finland, pages 7485, August 1923 2002.
[19] W. Cheung an d O.R. Zaiane. Incremental mining of
frequent patterns without candidate generation or support constraint. In
Proceedings of the Seventh International Database Engineering and Applications
Symposium (IDEAS 2003), Hong Kong, China, pages 111 116, July 1618, 2003.
[20] C. Creighton an d S. Hanash. Mining gene expression
databases for association rules. In Journal Bioinformatics, volume 19, pages
79-86, 2003.
[21] B.A Davey an d H.A. Priestley. Introduction to Lattices and
Order. Cambridge University Press, 2002.
[22] G. Dong, C. Jiang, J. Pei, J. Li, an d L. Wong. Mining
succinct systems of minimal generators of formal concepts. In Proceedings of
10th International Conference on Database Systems for Advanced Applications
(DASFAA 2005), Beijing, China, pages 175187, April 2005.
[23] A. Le Floc,h, C. Fisette, R. Missaoui, P.
Valtchev, an d R. Go din. JEN : un algorithme efficace de construction de
générateurs pour l,i dentification des regles
d,association. Numéro spécial de la revue des
Nouvelles Technologies de l'Information, 1(1) :135-146, 2003.
[24] J. M. Franco. Le Data Warehouse Le Data Mining.
Eyrolles, 1999.
[25] W. J. Frawley, G. Piatetsky-Shapiro, an d C. J. Matheus.
Knowledge discovery in databases - an overview. Artificial Intelligence
Magazine, 13 :5770, 1992.
[26] H. Fu an d E. Mephu Nguifo. Etude et conception
d,algorithmes de génération de concepts formels. In
J.-F. Boulicault an d B. Crémilleux, editors, Revue d'Ingénierie
des Systêmes d'Information (ISI), Hermês-Lavoisier, volume 9, pages
109-132, 2004.
[27] B. Ganter an d R. Wille. Formal Concept Analysis.
Springer-Verlag, 1999.
[28] K. Geurts. Traffic accidents data set. In B. Goethals an
d M. J. Zaki, editors, Proceedings of the IEEE ICDM Workshop on Frequent
Itemset Mining Implementations (FIMI'03), volume 90 of CEUR Workshop
Proceedings, Melbourne, Florida, USA, November 19, 2003.
[29] R. Go din, R. Missaoui, an d H. Alaoui. Incremental
concept formation algorithms base don Galois (concept) lattices. Journal of
Computational Intelligence, 11(2) :246267, May 1995.
[30] G. Grahne an d J. Zhu. Efficiently using prefix-trees in
mining frequent itemsets. In B. Goethals an d M. J. Zaki, editors, Proceedings
of the IEEE ICDM Workshop on Frequent Itemset Mining Implementations (FIMI'03),
volume 90 of CEUR Workshop Proceedings, Melbourne, Florida, USA, November 19,
2003.
[31] J. L. Guigues an d V. Duquenne. Familles minimales
d,implications informatives résultant d,un tableau
de données binaires. Mathématiques et Sciences Humaines, 24(95)
:518, 1986.
[32] T. Hamrouni, S. BenYahia, an d Y. Slimani. PRINCE :
Extraction optimisée des bases génériques de regles sans
calcul de fermetures. In Proceedings of the 23rd International Conference
INFORSID, Inforsid Editions, Grenoble, France, pages 353368, 2427 Mai 2005.
[33] T. Hamrouni, S. BenYahia, an d Y. Slimani. PRINCE : An
algorithm for generating rule bases without closure computations. In A Min Tjoa
an d J. Trujillo, editors, Proceedings of the 7th International Conference on
Data Warehousing and Knowledge Discovery (DaWaK
2005), Springer-Verlag, LNCS, volume 3589, Copenhagen, Denmark,
pages 346355, August 22-26, 2005.
[34] J. Han, J. Pei, an d Y. Yin. Mining frequent patterns
without candidate generation. In Proceedings of the ACM-SIGMOD Intl. Conference
on Management of Data (SIGMOD'00), Dallas, Texas, USA, pages 112, May 2000.
[35] J. Han, J. Pei, Y. Yin, an d R. Mao. Mining frequent
patterns without candidate generation : A frequent-pattern tree approach. In
Data Mining and Knowledge Discovery, volume 8, pages 53-87, 2004.
[36] J. Hipp, U. Giintzer, an d G. Nakhaeiza deh. Algorithms
for association rule mining - a general survey an d comparison. In ACM-SIGKDD
Explorations, New York, USA, volume 2, pages 5864, July 2000.
[37] W. A. Koesters an d W. Pijls. APRIORI, a depth first
implementation. In B. Goethals and M. J. Zaki, editors, Proceedings of the IEEE
ICDM Workshop on Frequent Itemset Mining Implementations (FIMI'03), volume 90
of CEUR Workshop Proceedings, Melbourne, Florida, USA, November 19, 2003.
[38] M. Kryszkiewicz. Representative association rules an d
minimum condition maximum conse-
quence association rules. In Proceedings of Second European
Symposium on Principles
of Data Mining and Knowledge Discovery (PKDD), 1998, LNCS,
volume 1510, Springer-
Verlag, Nantes, France, pages 361369, 1998.
[39] M. Kryszkiewicz. Concise representation of frequent
patterns base don disjunction-free generators. In Proceedings of the 1st IEEE
International Conference on Data Mining (ICDM), San Jose, California, USA,
pages 305312, 2001.
[40] M. Kryszkiewicz. Concise representation of frequent
patterns an d association rules. Habilitation thesis, Institute of Computer
Science, Warsaw University of Technology, Poland, August 2002.
[41] M. Kryszkiewicz. Concise representations of association
rules. In D. J. Hand, N.M. Adams, an d R.J. Bolton, editors, Proceedings of
Exploratory Workshop on Pattern Detection and Discovery in Data Mining (ESF),
Springer-Verlag, LNAI, volume 2447, London, UK, pages 92109, 2002.
[42] R. Lefebure an d G. Venturi. Le Data Mining. Eyrolles,
1999.
[43] C. Lucchese, S. Orlando, an d R. Perego. Mining frequent
close d itemsets without duplicates generation. Technical Report 13,
I.S.T.I.-C.N.R., Italy, 2004.
[44] C. Lucchesse, S. Orlando, an d R. Perego. DCI-CLOSED : a
fast an d memory efficient algorithm to mine frequent close d itemsets. In B.
Goethals, M. J. Zaki, an d R. Bayar do,
editors, Proceedings of the IEEE ICDM Workshop on Frequent
Itemset Mining Implementations (FIMI'04), volume 126 of CEUR Workshop
Proceedings, Brighton, UK, November 1st 2004.
[45] M. Luxenburger. Implications partielles dans un contexte.
Mathematiques et Sciences Humaines, 29(113) :35-55, 1991.
[46] A. M. Mueller. Fast sequential an d parallel algorithms
for association rules mining : a comparison. Technical Report CS-TR-3515,
Faculty of the Graduate School of the University of Maryland-College Park, USA,
October 1995.
[47] N. Pasquier. Datamining : Algorithmes
d,extraction et de reduction des regles d,association
dans les bases de donnees. These de doctorat, Ecole Doctorale Sciences pour
l,Ingenieur de Clermont Ferran d, Universite Clermont Ferran d II,
France, Janvier 2000.
[48] N. Pasquier, Y. Basti de, R. Taouil, an d L. Lakhal.
Pruning close d itemset lattices for association rules. In M. Bouzeghoub,
editor, Proceedings of 14th Intl. Conference Bases de Donnees Avancees,
Hammamet, Tunisia, pages 177196, October 2630, 1998.
[49] N. Pasquier, Y. Basti de, R. Taouil, an d L. Lakhal.
Efficient mining of association rules using close d itemset lattices. Journal
of Information Systems, 24(1) :25-46, 1999.
[50] N. Pasquier, Y. Basti de, R. Touil, an d L. Lakhal.
Discovering frequent close d itemsets for association rules. In C. Beeri an d
P. Buneman, editors, Proceedings of 7th International Conference on Database
Theory (ICDT'99), LNCS, volume 1540, Springer-Verlag, Jerusalem, Israel, pages
398416, January 1999.
[51] J. Pei, J. Han, an d R. Mao. CLOSET : An efficient
algorithm for mining frequent closed itemsets. In Proceedings of the ACM-SIGMOD
DMKD'00, Dallas, Texas, USA, pages 2130, 2000.
[52] J. L. Pfaltz an d C. M. Taylor. Scientific knowledge
discovery through iterative transformation of concept lattices. In Proceedings
of Workshop on Discrete Applied Mathematics in conjunction with the 2nd SIAM
International Conference on Data Mining, Arlington, Virginia, USA, pages 6574,
2002.
[53] A. Pietracaprina an d D. Zon dolin. Mining frequent
itemset using Patricia Tries. In B. Goethals an d M. J. Zaki, editors,
Proceedings of the IEEE ICDM Workshop on Frequent Itemset Mining
Implementations (FIMI'03), volume 90 of CEUR Workshop Proceedings, Melbourne,
Florida, USA, November 19, 2003.
[54] A. Salleb. Recherche de motifs frequents pour
l,extraction de regles d,association et de
caracterisation. These de doctorat, Laboratoire d,Informatique Fon
damentale d,Orleans LIFO, Université
d,Orléans, France, Décembre 2003.
[55] G. Stumme, R. Taouil, Y. Basti de, N. Pasquier, an d L.
Lakhal. Fast computation of concept lattices using data mining techniques. In
M. Bouzeghoub, M. Klusch, W. Nutt, an d U. Sattler, editors, Proceedings of 7th
Intl. Workshop on Knowledge Representation Meets Databases (KRDB'00), Berlin,
Germany, pages 129-139, 2000.
[56] G. Stumme, R. Taouil, Y. Basti de, N. Pasquier, an d L.
Lakhal. Intelligent structuring and reducing of association rules with formal
concept analysis. In F. Baader., G. Brewker, and T. Eiter, editors, Proceedings
of KI'2001 conference, LNAI, volume 2174, Springer-Verlag, Heidelberg, Germany,
2001.
[57] G. Stumme, R. Taouil, Y. Basti de, N. Pasquier, an d L.
Lakhal. Computing iceberg concept lattices with TITANIC. Journal on Knowledge
and Data Engineering (KDE), 2(42) :189222, 2002.
[58] R. Taouil. Algorithmique du treillis des fermes :
application a l,analyse formelle de concepts et aux bases de
donnees. These de doctorat, Ecole Doctorale Sciences pour
l,Ingenieur de Clermont?Ferran d, Universite Blaise Pascal, France,
Janvier 2000.
[59] H. Toivonen. Sampling large databases for association
rules. In Proceedings of the 22th Intl. Conference on Very Large Databases,
Bombay, India, pages 134145, September 1996.
[60] T. Uno, T. Asai, Y. Uchida, an d H. Arimura. LCM : An
efficient algorithm for enumerating
frequent close d item sets. In B. Goethals an d M. J. Zaki,
editors, Proceedings of the IEEE
ICDM Workshop on Frequent Itemset Mining Implementations
(FIMI'03), volume 90 of
CEUR Workshop Proceedings, Melbourne, Florida, USA, November 19,
2003.
[61] T. Uno, T. Asai, Y. Uchida, an d H. Arimura. An
efficient algorithm for enumerating closed patterns in transaction databases.
Journal of Discovery Science, LNAI, volume 3245, pages 16-31, 2004.
[62] T. Uno, M. Kiyomi, an d H. Arimura. LCM ver. 2 :
Efficient mining algorithms for
frequent/closed/maximal itemsets. In B. Goethals, M. J. Zaki, an
d R. Bayar do, editors,
Proceedings of the IEEE ICDM Workshop on Frequent Itemset Mining
Implementations
(FIMI'04), volume 126 of CEUR Workshop Proceedings, Brighton,
UK, November 1st, 2004.
[63] P. Valtchev, R. Missaoui, R. Go din, an d M. Meri dji.
Generating frequent itemsets incrementally : two novel approaches base don
Galois lattice theory. Journal Expt. Theoretical Artificial Intelligence, 14(1)
:115142, 2002.
[64] P. Valtchev, R. Missaoui, an d P. Lebrun. A fast
algorithm for building the Hasse diagram of a Galois lattice. In Proceedings of
the Colloque LaCIM 2000, Montreal, Canada, pages 293306, September 2000.
[65] J. Wang, J. Han, an d J. Pei. CLOSET+ : Searching for
the best strategies for mining frequent close d itemsets. In Proceedings of the
Ninth ACM-SIGKDD International Conference on
Knowledge Discovery and Data Mining (KDD'03), Washington D. C.,
USA, pages 236245, August 24-27, 2003.
[66] R. Wille. Restructuring lattices theory : An approach base
don hierarchies of concepts. I. Rival, editor, Ordered Sets, Dordrecht-Boston,
pages 445470, 1982.
[67] M. J. Zaki. Mining non-redundant association rules. In Data
Mining and Knowledge Discovery, volume 9, pages 223-248, 2004.
[68] M. J. Zaki an d K. Gouda. Fast vertical mining using
Diffsets. Technical report, Computer Science Dept., Rensselaer Polytechnic
Institute, USA, March 2001.
[69] M. J. Zaki an d C. J. Hsiao. CHARM : An efficient
algorithm for close d itemset mining. In Proceedings of the 2nd SIAM
International Conference on Data Mining, Arlington, Virginia, USA, pages 34-43,
April 2002.
[70] M. J. Zaki, S. Parthasarathy, M. Ogihara, an d W. Li.
New algorithms for fast discovery of association rules. In D. Heckerman, H.
Mannila, an d D. Pregibon, editors, Proceedings of the 3rd International
Conference on Knowledge Discovery and Data Mining (KDD '97), Newport Beach,
California, USA, pages 283290, August 1997.
| 
