Memoire Online - Extraction des bases génériques informatives de règles sans calcul de fermetures

Dans cette section, nous allons introduire un nouvel algorithme, appele PRINCE, dont l'objectif principal est de pallier la principale lacune des algorithmes dedies a l'extraction des itemsets fermes frequents, cad ne pas construire la relation d'ordre partiel. La principale originalite de PRINCE est qu'il construit une structure partiellement ordonnee appelee treillis des generateurs minimaux [7]. Dans cette structure, l'ordre partiel est maintenu non plus entre les itemsets fermes frequents mais entre leurs generateurs minimaux associes. De plus, PRINCE met en place un mecanisme de gestion des classes d'equivalence permettant de generer la liste integrale des itemsets fermes frequents sans duplication et sans recours aux tests de couvertures. Il permet aussi de reduire d'une maniere notable le cofit du calcul des fermetures et ceci en utilisant les notions de blo queur minimal et de face introduites par Pfaltz et Taylor dans [52].

support minsup et le seuil minimal de confiance minconf. Il donne en sortie : la liste des itemsets fermes frequents, leurs generateurs minimaux associes ainsi que les bases generiques de regles. PRINCE opere en trois etapes successives :

Avant de commencer la description de cette premiere etape, nous allons commencer par introduire la definition d'un treillis des generateurs minimaux :

Definition 6 [7] Un treillis des generateurs minimaux est une structure equivalente au treillis d'Iceberg tel que dans cha que classe d'equivalence, nous ne trouvons que les generateurs minimaux frequents correspondants.

En adoptant la strategie "Generer-et-tester", l'algorithme PRINCE parcourt l'espace de recherche par niveau pour determiner l'ensemble des generateurs minimaux frequents, note gMFK, ainsi que la bordure negative des generateurs minimaux, notee gBd^-. PRINCE utilise, dans cette etape, les memes strategies d'elagage que TITANIC, cad minsup, l'ideal d'ordre regissant des generateurs minimaux frequents et le support estime.

Le pseudo-code relatif a cette etape est donne par la procedure GEN-GMs (cf. Algorithme 1). Les notations utilisees sont resumees dans le tableau 3.1.

La procedure GEN-GMs prend en entree le contexte d'extraction 1C et le support minimal minsup. Elle donne en sortie l'ensemble des generateurs minimaux frequents gMFK de faZon a pouvoir les parcourir par ordre decroissant de leurs supports respectifs lors de la deuxieme^etape de l'algorithme PRINCE. gMFK est alors considere comme etant divise en plusieurs sous-ensembles. Chaque sous-ensemble est caracterise par la meme valeur du support. Ainsi, chaque fois qu'un generateur minimal frequent est determine, il est ajoute a l'ensemble representant son support. La procedure GEN-GMs garde aussi la trace des generateurs minimaux infrequents, formant la bordure negative gBd^-, afin de les utiliser lors de la deuxieme etape.

k : un compteur qui indique l'iteration courante. Durant la ki`eme iteration, tous les k-generateurs minimaux sont determines.

GMCk : ensemble des k-generateurs minimaux candidats.
GMFk : ensemble des k-generateurs minimaux frequents.

GMFK : ensemble des generateurs minimaux frequents tries par ordre decroissant du support.

Chaque element c de GMCk est aussi caracterise par un support estime (le champ support-estime ) et qui sera utilise pour eliminer les candidats non generateurs minimaux.

CALCUL-SUPPORT (GMC1); Ø.support-réel =1O1; GMF0 = {Ø}; pour chaque (c ? GMC1) faire si (c.support-réel = 1O1) alors ã(Ø)=ã(Ø) ? c;

si (c.support-réel = minsup) alors c.sous-ens-directs ={Ø}; GMF1=GMF1 ? c;

/* Phase 2 : Vérification de l'idéal d'ordre régissant les générateurs minimaux fréquents. */

pour chaque (c ? GMC(k+1)) faire c.support-estimé = 1O1; /* support maximal possible */ pour chaque (c₁ tel que |c₁| = k et c₁ ? c) faire si (c1 ?/ GMFk) alors

c.support-estimé = min(c.support-estimé, c₁.support-réel ); c.sous-ens-directs = c.sous-ens-directs ? c₁;

CALCUL-SUPPORT (GMC(k+1)); pour chaque (c ? GMC(k+1)) faire si (c.support-réel c.support-estimé et c.support-réel = minsup) alors

(ligne 3). Le support des items est alors calculé via un accès au contexte d'extraction (ligne 4). Le support de l'ensemble vide est égal au nombre de transactions du contexte d'extraction, cad 1O1 (ligne 5). L'ensemble vide, étant le générateur minimal fréquent de taille ⁰, est inséré dans gmF0 (ligne 6). Pour tout 1-itemset c, nous distinguons les trois cas suivants (lignes 7-15) :

Ensuite, le parcours se fait par niveau. Pour cela, nous utilisons la procédure GEN-GMSSUIVANT (lignes 16-17) dont le pseudo-code est donné par l'algorithme 2. La procédure GEN-GMS-SUIVANT prend en entrée l'ensemble des générateurs minimaux fréquents de taille k et retourne l'ensemble des générateurs minimaux fréquents de taille (k+1). La première étape de l'algorithme PRINCE prend fin lorsqu'il n'y a plus de candidats a générer. Elle retourne alors l'ensemble des générateurs minimaux fréquents gmFK trié par ordre décroissant des supports (ligne 18).

La première phase de la procédure GEN-GMS-SUIVANT consiste a effectuer la jointure des générateurs minimaux fréquents d'une itération k pour obtenir l'ensemble des candidats (k+1)-générateurs minimaux, cad gmC(k+1) (lignes 3-4). Lors de la deuxième phase et pour chaque candidat c E gmC(k+1), nous testons s'il vérifie l'idéal d'ordre des générateurs minimaux fréquents (lignes 5-14). En même temps, nous calculons le support estimé de c et qui est égal au minimum des supports de ses sous-ensembles de taille k (ligne 13). Des liens vers ces derniers sont stockés dans le champ sous-ens-directs et qui seront utilisés dans la seconde étape de l'algorithme PRINCE (ligne 14). Si c ne vérifie pas l'idéal d'ordre alors c est éliminé de gmC(k+1) (lignes 9-12). Une fois le test de l'idéal d'ordre effectué, nous entamons la troisième phase (lignes 15-22). Ainsi, un accès au contexte d'extraction permettra de calculer les supports réels des candidats retenus dans gmC(k+1) (ligne 16). Une fois cet accès effectué, le support réel de chaque candidat c de gmC(k+1), est comparé a son support estimé (lignes 17-22). Si ces derniers sont égaux, c

n'est pas un generateur minimal. Sinon, c est un generateur minimal et la comparaison de son support reel avec minsup permettra de le classer parmi les generateurs minimaux frequents ou parmi ceux infrequents (lignes 18-22). Apres l'execution de ces trois phases, la procedure GEN-GMS-SUIVANT retourne l'ensemble des generateurs minimaux frequents de taille (k+1) (ligne 23).

Dans la suite, nous allons noter par support, au lieu de support-reel, le champ contenant le support reel de chaque generateur minimal etant donne que nous n'avons plus a distinguer entre le support reel et le support estime d'un itemset.

L'objectif de cette etape est d'organiser les generateurs minimaux frequents sous forme d'un treillis des generateurs minimaux et sans effectuer un acces supplementaire au contexte d'extraction. Pour atteindre cet objectif, les listes des successeurs immediats⁽²⁾ seront modifiees d'une maniere iterative. Ainsi, nous parcourons l'ensemble trie GMFK en introduisant un par un les generateurs minimaux frequents dans le treillis des generateurs minimaux.

Chaque generateur minimal frequent g de taille k (k = 1) est introduit dans le treillis des generateurs minimaux en le comparant avec les successeurs immediats de ses sous-ensembles de taille (k-1). Rappelons que des liens vers ces derniers ont ete stockes dans le champ sous-ens-directs des la premiere etape. Ceci est base sur la propriete d'isotonie de l'operateur de fermeture [21]. En effet, si g₁ est inclus dans g tel que Ig₁l--(k-1) alors la fermeture de g₁, ã(g₁), est incluse dans la fermeture de g, ã(g). Ainsi, la classe d'equivalence a laquelle appartient g est un successeur -- pas forcement immediat -- de la classe d'equivalence a laquelle appartient g₁.

En comparant g a la liste des successeurs immediats de g₁, disons L, deux cas sont a distinguer. Si L est vide alors g est simplement ajoute a L. Sinon, g est compare aux elements appartenant a L (cf. Proposition 3 ci-dessous). Pour chaque comparaison, les deux cas presentes dans la proposition 3 sont alors a distinguer en remplacant X par g et Y par un des elements de L.

Proposition 3 [32] Soient X, Y ? GMFK, CX et CY dénotent leurs classes d'équivalence respectives :

Le calcul du support de (X ? Y ) se fait d'une maniere directe si (X ? Y ) est un générateur minimal. Dans ce cas, CX et CY sont incomparables. Sinon, la proposition 2 (cf. page 29) est appliquée. La recherche du support s'arrete des qu'un générateur minimal inclus dans (X ? Y ) et ayant un support inférieur strictement a celui de X et a celui de Y est trouvé. Dans ce cas, CX et CY sont incomparables.

Lors de ces comparaisons et pour éviter une des lacunes des algorithmes adoptant la stratégie "Générer-et-tester", a savoir le calcul redondant des fermetures, PRINCE utilise deux fonctions qui se completent. Ces fonctions permettent de maintenir la notion de classe d'équivalence tout au long du traitement. A cet effet, chaque classe d'équivalence C sera caractérisée par un représentant, qui est le premier générateur minimal fréquent introduit dans le treillis des générateurs minimaux. Tout générateur minimal fréquent g est initialement considéré comme représentant de C_g et le restera tant qu'il n'est pas comparé a un générateur minimal fréquent précédemment introduit dans le treillis des générateurs minimaux et appartenant a C_g. Les deux fonctions sont décrites dans ce qui suit [33, 32] :

Le pseudo-code de la deuxieme etape est donne par la procedure GEN-ORDRE (cf. Algorithme 3). L'ensemble trie GMFK contient les generateurs minimaux frequents ex-traits a partir du contexte d'extraction K. En plus des champs utilises dans la premiere etape (cf. Tableau 3.1 page 42), a chaque element g de GMFK est associe le champ succs-immediats pour contenir la liste des successeurs immediats de g. A la fin de l'execution de la procedure GEN-ORDRE, cette liste est vide si g n'est pas le representant de sa classe d'equivalence ou si g appartient a une classe d'equivalence n'ayant pas de successeurs. Sinon, cette liste ne contiendra que des representants.

La procedure GEN-ORDRE introduit un generateur minimal frequent g dans le treillis des generateurs minimaux en le comparant aux listes des successeurs immediats de ses sous-ensembles de taille (k-1) (ligne 3). Soit g₁ un des sous-ensembles de g (ligne 4). La procedure GEN-ORDRE retrouve le representant de la classe d'equivalence de g₁ moyennant l'utilisation de la fonction REPRESENTANT (ligne 5). Soit L la liste des successeurs immediats de Cg₁ stockee au niveau de son representant R. L est donc egale a R.succs-immediats . L'ordre decroissant par rapport aux supports, impose dans l'ensemble GMFK, permet de ne distinguer que deux cas dans chaque comparaison de g avec un element de L. En effet, si nous appelons g₂ un des elements de L, alors si la classe

d'equivalence de g et celle de g₂ sont comparables, g et g₂ doivent verifier une des deux conditions presentees dans la proposition 3 (avec X=g, Y=g₂ et Supp(g)=Supp(g₂)). Si aucune de ces deux conditions n'est verifiee, g et g₂ appartiennent a des classes d'equivalence incomparables. Si g et g₂ verifient la premiere condition de la proposition 3, alors g et g₂ appartiennent a la meme classe d'equivalence (g₂ est le representant de C_g) et les traitements relatifs a la gestion de la classe d'equivalence C_g sont realises moyennant un appel a la fonction GESTTON-CLASSE-EQUT (lignes 7-8). Si g et g₂ verifient la deuxieme condition de la proposition 3, alors C_g est un successeur de C_g₂ et nous comparons d'une maniere recursive g a la liste des successeurs immediats de g₂ (lignes 10-11). Pour le reste des elements de L, disons L₁, nous ne comparons g qu'aux elements ayant un support strictement superieur a celui de g (ligne 12). En effet, g n'appartient a aucune des classes d'equivalence representees par les elements de L₁ car sinon il ne serait pas un successeur de g₂. Si nous appelons g₃ un des elements de L₁, et si C_g et Cg₃ sont comparables, C_g ne peut etre qu'un successeur de Cg₃ et nous comparons la liste des successeurs immediats de g₃ a g. Si la classe d'equivalence de g est incomparable avec celles de tous les elements de L, alors g est ajoute a L (ligne 13-14). Il faut noter que ces comparaisons sont de nombre fini etant donne que le nombre d'elements de chaque liste de successeurs immediats est fini et il en est de meme pour le nombre de generateurs minimaux frequents dejà introduits dans le treillis des generateurs minimaux.

Remarque 1
· Notons que si nous avons opte pour n'importe quel autre ordre dans le tri de GMFK (par exemple, tri par ordre croissant par rapport aux supports) et si g est incomparable avec tous les elements de L, les comparaisons de g avec les listes des successeurs immediats des representants formant L seraient dans ce cas obligatoires. En effet, deux classes d'equivalence incomparables (celle de g et celle d'un representant appartenant à L) peuvent avoir des successeurs en commun existants dejà dans le treillis des generateurs minimaux. Ainsi, n'importe quel autre choix de tri augmenterait considerablement le nombre, et par consequent le coat, des comparaisons pour construire le treillis des generateurs minimaux.

· L'utilisation de la bordure negative des generateurs minimaux GBd^- dans le mecanisme de comptage par inference [6J est une consequence du fait que son union avec l'ensemble des generateurs minimaux frequents GMFK forme une representation concise de l'ensemble des itemsets frequents [39, 40J. Ainsi, en utilisant l'ensemble resultat de cette union, nous pouvons retrouver le support de tout itemset sans effectuer un accès au contexte d'extraction [39, 40J.

Resultats : - Les elements de GMFK ordonnes partiellement sous forme d'un treillis des générateurs minimaux.

pour chaque (g ? GMFK) faire pour chaque (g₁ ? g.sous-ens-directs) faire R = REPRESENTANT (g₁); pour chaque (g₂ ? R.succs-immédiats ) faire si (g.support = g₂.support = Supp(g ? g₂)) alors GESTION-CLASSE-EQUIV (g,g₂); /*g,g₂ ? C_g et g₂ est le representant de C_g*/

si (g.support < g₂.support et g.support = Supp(g ?g₂)) alors g est compare a g₂.succs-immédiats ; /* Pour le reste des elements de R.succs-immédiats , g n'est compare qu'avec tout g₃ tel que g₃.support > g.support ; */

si (? g₂ ? R.succs-immédiats, C_g et C_g₂ sont incomparables) alors R.succs-immédiats = R.succs-immédiats ? {g};

3.2.3 Extraction des bases generiques informatives de regles

Dans cette etape, PRINCE extrait les regles generiques informatives valides formees par l'union de la base generique de regles exactes et de la reduction transitive de la base informative de regles approximatives. Ainsi, pour chaque classe d'equivalence, PRINCE retrouve l'itemset ferme frequent correspondant via l'application de la proposition 4 don-nee ci-dessous. La preuve de la proposition 4 necessite d'introduire les definitions et le theoreme suivants :

Definition 8 Soient f, f₁ ? IFFK. Si f couvre f₁ dans le treillis d'Iceberg ( ^àL, ? ) alors la face de f par rapport a f₁, notée face~f&f₁~, est égale a : face(fIf1) = f - f1.

Theoreme 2 Soient f ? IFFK et GMf l'ensemble de ses générateurs minimaux. Si f₁ ? IFFK tel que f couvre f₁ dans le treillis d'Iceberg ( ^àL,? ) alors face(fIf₁) est un blo queur minimal de GMf [527.

Proposition 4 Soient f et f₁ ? IFFK tels que f couvre f₁ dans le treillis d'Iceberg ( ^àL,? ). Soit GMf l'ensemble des générateurs minimaux de f. Alors, l'itemset fermé fréquent f est égal a : f = ?{g|g ? GMf} ? f₁.

Preuve.Etant donne que l'union des elements de GMf est un bloqueur de GMf, la face(fIf₁), qui est un bloqueur minimal pour GMf d'apres le Theoreme 2, est incluse dans l'union des elements de GMf. Ainsi, il suffit de calculer l'union de f₁ avec les elements de GMf pour retrouver f.

Il est a noter que Proposition 4 a pour avantage d'assurer l'extraction sans redondance de l'ensemble des itemsets fermes frequents. Le pseudo-code de cette etape est donne par la procedure GEN-BGRs (cf. Algorithme 4)⁽³⁾. Nous utilisons les mêmes notations que celles des algorithmes precedents, auxquelles nous ajoutons le champ iff pour chaque element de GMFK. Ainsi pour chaque generateur minimal frequent g, ce champ permet de stocker l'itemset ferme frequent correspondant a C_g si g est son representant. Dans la procedure GEN-BGRs, L₁ designe la liste des classes d'equivalence a partir desquelles sont extraites les regles d'association informatives. Par L₂, nous designons la liste des classes d'equivalence qui couvrent celles formant L₁.

L'ensemble des regles informatives exactes BG est initialement vide (ligne 3). Il en est de même pour l'ensemble des regles informatives approximatives RI (ligne 4). Le parcours du treillis des générateurs minimaux s'effectue d'une maniere ascendante en partant de la classe d'equivalence dont le generateur est l'ensemble vide (notee CØ). Ainsi, L₁ est initialisee a l'ensemble vide (ligne 5). Rappelons que la fermeture de l'ensemble vide a dejà ete calculee des la premiere etape en collectant les items qui se repetent dans toutes

les transactions (cf. ligne 8-9 de l'algorithme 1 page 43). La liste L₂ est initialement vide (ligne 6). Les traitements de cette étape s'arrêtent lorsqu'il n'y a plus de classes d'équivalence à partir desquelles seront extraites des regles génériques (ligne 7). Si la fermeture de l'ensemble vide n'est pas nulle, la regle exacte informative mettant en jeu l'ensemble vide et sa fermeture sera extraite (ligne 9-10). Ayant l'ordre partiel construit, GEN-BGRs extrait les regles approximatives informatives valides mettant en jeu l'ensemble vide et les itemsets fermés fréquents de la couverture supérieure de CØ (lignes 11-16). Ces fermetures sont retrouvées en utilisant la proposition 4 en utilisant les générateurs minimaux fréquents de chaque classe d'équivalence et la fermeture de l'ensemble vide (ligne 11). Cette couverture supérieure est stockée afin que le même traitement soit réalisé pour les classes d'équivalence la composant (ligne 12). Une fois les traitements relatifs à la classe d'équivalence de l'ensemble vide terminés, L₁ prendra pour valeur le contenu de L₂ (ligne 17) afin de ré-appliquer le même processus aux classes d'équivalence qui sont des successeurs immédiats de CØ. L₂ est ré-initialisée au vide (ligne 18) et contiendra les successeurs immédiats des classes d'équivalence contenues dans L₁. Etant donné qu'une classe d'équivalence peut avoir plusieurs prédécesseurs immédiats, un test est réalisé pour vérifier qu'elle n'a pas déjà été insérée dans L₂. Ce test consiste à vérifier si l'itemset fermé fréquent correspondant a déjà été calculé (ligne 12). De la même maniere, GEN-BGRs traite les niveaux supérieurs du treillis des générateurs minimaux jusqu'à atteindre ses sommets (cad les classes d'équivalence n'ayant pas de successeurs). L₁ serait alors vide et la condition de la ligne 7 ne sera plus vérifiée. Ainsi, la troisieme étape de l'algorithme PRINCE prend fin et toutes les regles génériques sont extraites.

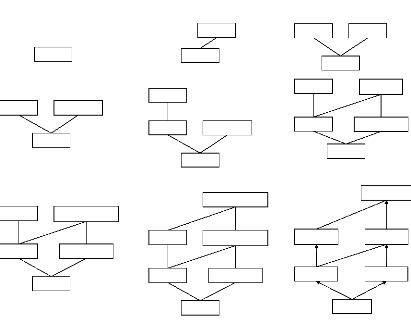
Exemple 4 Afin d'illustrer le déroulement de l'algorithme PRINCE, considérons le contexte d'extraction K donné par la Figure 3.1 pour minsup = 2 et minconf = 0,5. La première étape permet de déterminer l'ensemble des générateurs minimaux GMFK trié, ainsi que la bordure négative GBd^-. GMFK = {(Ø,5),(B,4),(C,4), (E,4), (A,3), (BC,3),(CE,3), (AB,2), (AE,2)} et GBd^-={ (D,1)}. Dans la deuxième étape, PRINCE parcourt GMFK en comparant cha que générateur minimal fréquent g de taille k (k = 1) aux listes des successeurs immédiats de ses sous-ensembles de taille (k-1). L'ensemble vide, n'ayant aucun sous-ensemble, est introduit directement dans le treillis des générateurs minimaux (cf. Figure 3.2.a). Ensuite, B est ajouté a Ø.succs-immédiats (cf. Figure 3.2.b), la liste des successeurs immédiats du Ø, initialement vide. Ensuite, C sera comparé a B. BC étant un générateur minimal, CB et CC sont alors incomparables et C est ajouté a Ø.succs-immédiats (cf. Figure 3.2.c). E est alors comparé a cette liste. En comparant E

a B, E.support = B.support = Supp(BE) et donc E ? CB dont B est le représentant (cf. Figure 3.2.d). La fonction GESTION-CLASSE-EQUIV est alors appli quée et ceci en remplaçant les occurrences de E par B dans des listes des successeurs immédiats (dans ce cas, il n'y a aucune occurrence) et en poursuivant les comparaisons avec B au lieu de E (dans ce cas, il n'y a plus de comparaisons a faire via E). Les traitements s'arrétent alors pour E. A ce moment du traitement, Ø.succs-immédiats = {B,C}. Le générateur minimal fréquent A est alors comparé a B. Comme AB ? GMFK, CB et CA sont incomparables. Par contre, en comparant A et C, A.support < C.support et A.support = Supp(AC) et donc CA est un successeur de CC. Le générateur minimal A est tout simplement ajouté a C.succs-immédiats étant donné qu'elle est encore vide (cf. Figure 3.2.e). BC est comparé aux listes des successeurs immédiats de B et de C. La liste des successeurs immédiats de B est vide, BC est alors ajouté. La liste des successeurs immédiats de C contient A. Le générateur minimal fréquent BC est alors comparé a A et comme BC.support = A.support mais BC.support =~ Supp(ABC), CBC et CA sont incomparables et BC est donc ajouté a C.succs-immédiats (cf. Figure 3.2.f ). CE est comparé aux listes des successeurs immédiats de C et de E. Celle de C contient A et BC. CCE et CA sont incomparables, puis que CE.support = A.support mais CE.support =~ Supp(ACE). En comparant CE a BC, CE.support = BC.support = Supp(BCE) alors l'itemset CE va étre affecté a la classe d'équivalence de BC et les fonctions de gestion des classes d'équivalence sont invo quées (cf. Figure 3.2.g). En particulier, les comparaisons de CE aux successeurs immédiats de CE seront faites avec BC. Comme CE a pour représentant B, BC est donc comparé aux éléments de B.succs-immédiats. Cependant, comme B.succs-immédiats ne contient que BC alors les comparaisons se terminent. Le méme traitement est appli qué pour AB et AE. Ainsi, la procédure de construction de l'ordre partiel prend fin. Le treillis des générateurs minimaux obtenu est donné par la figure 3.2.h. Pour la dérivation des règles généri ques, le treillis des générateurs minimaux est parcouru d'une manière ascendante a partir de Co. Comme ã(Ø) = Ø, il n'y a donc pas de règle exacte informative relative a Co. Ø.succs-immédiats={B,C}. L'itemset fermé fréquent correspondant a CB est alors retrouvé et est égal a BE (cf. Figure 3.2.i). La règle informative approximative valide Ø BE de support 4 et de confiance 0,8 sera alors extraite. Il en est de méme pour la règle Ø C, ayant les mémes valeurs de support et de confiance que la précédente. De la méme manière et a partir de CB et CC, le parcours du treillis se fait d'une facon ascendante jus qu'a extraire toutes les règles d'association informatives valides.

A la fin de l'exécution de l'algorithme, nous obtenons le treillis d'Iceberg associé au

contexte d'extraction K (cf. Figure 3.2.i)⁽⁴⁾ ainsi que la liste les regles informatives valides, donn~e par la Figure 3.3.

Lors de la premiere etape, nous avons utilise un arbre prefixe (ou trie) pour stocker les generateurs minimaux retenus. L'utilisation d'un seul trie a ete motivee par le fait que^l'ensemble des generateurs minimaux GMK d'un contexte d'extraction K forme un ideal d'ordre. Ainsi, chaque nceud du trie represente un generateur minimal. Ceci a pour avantage de reduire la necessite en memoire centrale comparee a l'utilisation d'un trie pour cha que ensemble de generateurs minimaux de taille k donnee, comme c'est le cas pour les algorithmes CLOSE [49], A-CLOSE [50] et TITANIC [57]. En effet, l'utilisation d'un seul trie permet de reduire la redondance dans le stockage des informations relatives aux generateurs minimaux. Cependant, le fait d'utiliser un seul trie rend l'espace de recherche nettement plus grand lors de l'execution de quelques operations telles que la verification de l'ideal d'ordre des generateurs minimaux frequents oft la recherche des supports adequats dans la deuxieme etape de l'algorithme PRINCE.

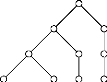
Un autre trie a ete utilise dans chaque iteration k, de la premiere etape, afin de calculer le support des candidats generateurs minimaux de taille k. La Figure 3.4 presente un trie qui stocke quatre candidats generateurs minimaux de taille 3 : ABC, ABD, A CD et BCD. Dans ce qui suit, nous donnons une presentation succincte de cette structure de donnees.

Un trie est un arbre de recherche, dont les donnees sont stockees d'une faZon condensee [12]. La structure de donnees trie etait a l'origine introduite pour stocker et pour recuperer les mots d'un dictionnaire [12]. Un trie est un arbre dirige du haut vers le bas comme dans le cas d'un arbre de hachage. Neanmoins, dans le cas d'un trie, nous ne distinguons pas entre un nceud interne et un nceud feuille contrairement au cas d'un arbre de hachage. En effet, dans ce dernier, le nceud interne est caracterise par une table de hachage et un nceud feuille contient un ensemble d'itemsets [14]. Dans un trie, la racine est consideree a une profondeur 0, et un nceud a une profondeur d ne peut pointer qu'aux nceuds de profondeur d + 1. Un pointeur est appele aussi branche ou lien, et est etiquete par une lettre. Si un nceud u pointe sur un nceud v, u est appele le parent de v et v un enfant de u.

Regles informatives approximatives
R₈ : Ø0,80 BE	R₁₃ : E0,75 BC
_R9 : Ø0,80 C	_R14 : A0,66 BCE
R10 : C0,75 A	R₁₅ : BC^0,66 AE
R11 : C0,75 BE	R₁₆ : CE^0,66 AB
R₁₂ : B0,75 CE
		A	B	C	D	E
1		×		×	×
2			×	×		×
3		×	×	×		×
4			×			×
5		×	×	×		×

FIG . 3.2 -- Construction du treillis des generateurs minimaux et le treillis d'Iceberg associes au contexte d'extraction K pour minsup2.

Chaque feuille l represente un mot qui est la concatenation des lettres qui se trouvent sur le chemin de la racine a l. Notons que si les premieres k lettres sont les memes pour deux mots, alors les premieres k branches sur leurs chemins sont aussi les memes [12].

La structure de donnees trie permet de stocker et de recuperer non seulement les mots mais n'importe quel ensemble E fini et ordonne. Dans ce cas, chaque lien est etiquete par un element de E et le trie contient un sous-ensemble F de E s'il y a un chemin oft les liens sont etiquetes par les elements de F dans l'ordre choisi.

Dans notre contexte, l'alphabet est l'ensemble (ordonne) des items I. Un k-itemset c : {i₁ < i₂ < i₃ < . . . < i_k} peut etre vu comme etant le mot i1i2i3 ...i_k compose des lettres de I. Ainsi, le chemin menant de la racine a chaque nceud du trie represente un (candidat) generateur minimal.

Plusieurs travaux ont etudie la structure de donnees trie. Nous mentionnons principalement les travaux de Bodon et al. Dans [14], Bodon et al. montrent l'interêt de l'utilisation de cette structure de donnees comparee a la structure de donnee d'arbre de hachage en considerant differents criteres, tels que la simplicite d'utilisation, l'extraction des informations, etc. Dans [12, 13], Bodon montre l'efficacite de la structure trie, appliquee à l'algorithme APRIORI [2], le premier a avoir introduit l'utilisation de l'arbre de hachage, durant l'etape de calcul des supports des itemsets.

Extraction des bases génériques informatives de règles sans calcul de fermetures

3.2 L 'algorithme PRINCE

3.2.3 Extraction des bases generiques informatives de regles