1.2. Eléments d'analyse des séries
temporelles :
Cette section est consacrée à une
présentation sommaire des techniques d'analyse des séries
chronologiques. Ce thème, à lui seul, peut faire l'objet de longs
développements et de nombreux ouvrages20 y sont
intégralement consacrés. Nous étudions en 1.2.1, les
caractéristiques statistiques en terme de stationnarité des
séries temporelles en présentant les différents tests
(Dickey-Fuller, corrélogramme, etc.) s'y rapportant. Puis en 1.2.3, nous
présentons différentes classes de modèles (AR, MA, ARMA)
en étudiant leurs propriétés. Enfin, la méthode Box
et Jenkins qui systématise une démarche d'analyse des
séries temporelles fait l'objet de la section 1.2.4.
1.2.1. Stationnarité :
1.2.1.1.Définition et propriétés
:
Avant le traitement d'une série chronologique, il
convient d'en étudier les caractéristiques stochastiques. Si ces
caractéristiques - c'est-à-dire son espérance et sa
variance - se trouvent modifiées dans le temps, la série
chronologique est considérée comme non stationnaire ; dans le cas
d'un processus stochastique invariant, la série temporelle est alors
stationnaire. De manière formalisée, le processus stochastique y,
est stationnaire si :
E ( yt )= E (yt + m )=
t et m, la moyenne est constante et
indépendante du temps ;
var (yt ) < t, la variance est finie et
indépendante du temps ;
cov ( yt ,yt+k ) = E[(yt -
) (yt+k - )] = Yk, la covariance est
indépendante du temps.
Il apparaît, à partir de ces
propriétés, qu'un processus de bruit blanc t
dans lequel les , sont indépendants et de même loi N(0,o ~) est
stationnaire.
Une série chronologique est donc stationnaire si elle
est la réalisation d'un processus stationnaire21. Ceci
implique que la série ne comporte ni tendance, ni saisonnalité et
plus généralement aucun facteur n'évoluant avec le
temps.
20 Pour un approfondissement de ce chapitre, se
référer au livre de Bourbonnais R. et Terraza M., Dunod, 2004.
21 Si les conditions énoncées
ci-dessous sont vérifiées, on dit que la série est
stationnaire de second ordre, ou encore faiblement stationnaire. Dans le cas
oü, aux conditions définies, s'ajoute la constante de la
distribution de probabilité, on parle de série strictement
stationnaire.
1.2.1.2. Fonctions d'autocorrélation simple et
partielle :
La fonction d'autocorrélation (FAC) est la fonction
notée k qui mesure la corrélation de la
série avec elle-même décalée de k
périodes, comme l'illustre le tableau 2.
Sa formulation est la suivante :
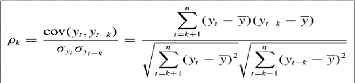
avec moyenne de la série calculée sur n -
k périodes, n= nombre d'observations. Nous pouvons en
déduire que :
0 = 1 et k = -k
Cette formule [1] est malaisée à manier
puisqu'elle exige de recalculer pour chaque terme k, les moyennes et
les variances, c'est pourquoi on lui préfère la fonction
d'autocorrélation d'échantillonnage :
Avec moyenne de la série calculée sur n
périodes.
Lorsque le nombre d'observations n est suffisamment
grand, les deux formules [1] et [2] donnent des résultats très
proches.
La fonction d'autocorrélation partielle (FAP)
s'apparente à la notion de corrélation partielle. Ainsi le
coefficient de corrélation partielle est défini comme
étant le calcul de l'influence de X1, sur X2, en
éliminant les influences des autres variables X3,
X4,...,Xk.
Tableau 2 : Exemple de calcul d'une fonction
d'autocorrélation
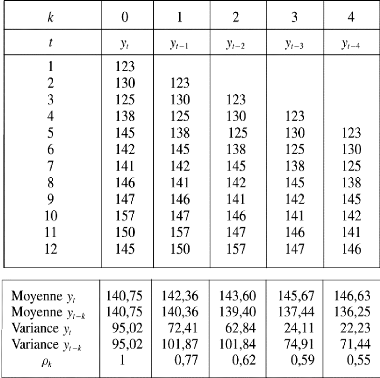
Source : Bourbonnais, Régis, Terraza,
Michel, «Analyse des séries temporelles», Dunod
2008
Par analogie, nous pouvons définir
l'autocorrélation partielle de retard k comme le
coefficient
de corrélation partielle entre yt, et
yt-k, c'est-à-dire comme étant la
corrélation entre yt, et yt-k,
l'influence des autres variables décalées de k
périodes (yt-1, yt-2,..., yt-k+1 ) ayant
été retirée.
Afin d'éviter par la suite toutes ambiguïtés
entre les deux fonctions d'autocorrélation, nous appelons fonction
d'autocorrélation simple, la fonction d'autocorrélation.
| 


