3.2.2. From consumers
According to Shuval et al., (1997) 10.8 mL of irrigation water
will be left on a 100 g lettuce after harvest. There are two days between
lettuce harvest and consumption (WHO, 2006a). The amount of lettuce consumed
per person per day was taken as 100 g at a rate of one lettuce per week per
consumerin developing country (Shuval et al., 1997);(Nana O.B. Ackerson and
Esi Awuah, 2012)such as Burkina Faso. Thus, a consumer can be exposed 52 times
per year.The exposure scenarios of different matrix for farmers and consumers
are summarized in table 3 below.
Table 3: Different exposure
scenarios and pathways which farmers and consumers can be exposed in different
cases
|
Target population
|
Matrix of manipulation
|
Exposure scenario
|
Quantityingested
|
Frequencyexposed (events/year)
|
|
Farmers
|
Compost
|
Handle without protection individual (glove, mask,...) before
to spread compost
|
10-100mga
|
5
|
|
Urine
|
Handle urine in the field with a small bucket and use this
hand to eat without washing it
|
0.43 mL*
|
15
|
|
Soil
|
Ingestion of soil contaminated with greywater, compost
orurine.
|
10-100mgb
|
20
|
|
Greywater
|
Ingestion of greywater from the irrigation system (watering
cans or bucket )
Accidental ingestion
|
1-2mLc
|
275
|
|
Consumers
|
Lettuceharvest
|
Consumers can eat lettuce without washing it
|
10.8mL/100gd
|
52
|
a=(Schönning et al., 2007) ;
b=(Haas et al., 1999) ; c=(Nana O.B. Ackerson and Esi
Awuah, 2012); d=(Shuval et al., 1997).*= Protocol of determination of
amount of urine ingested (annex 2).
3.3. Dose-response
assessment
For dose-response relationships, the beta-Poisson
dose-response model described by Haas et al., (1999)was used for
Salmonella, Ascaris. However, single-hit exponential dose-response can
be applied for Salmonella and Ascaris. Dose-response
parameters for exponential and beta-Poisson models from various enteric
pathogen ingestion studied by different authors were summarized in table 4
below. To calculate microbial risk, uncertain values (minimum and maximum
values) of pathogen amounts will use to evaluate risk for each treatment.
Single-hit exponential model:
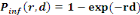 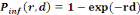 (Equation 5) (Equation 5)
Beta-Poisson model:
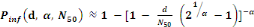 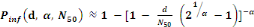 (Equation 6) (Equation 6)
Where 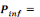 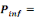 the probability of infection which is a function of r and d the probability of infection which is a function of r and d
  = empirical parameter assumed to be constant for any given
host and given pathogen picked to fit the data = empirical parameter assumed to be constant for any given
host and given pathogen picked to fit the data
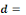 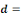 Mean ingested dose, N50= the median
dose, á andâ= slope parameters, which hold when
â=1 and á=â. Mean ingested dose, N50= the median
dose, á andâ= slope parameters, which hold when
â=1 and á=â.
The annual probability of infection is given by:
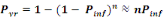 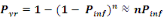 (Equation 7) (Equation 7)
Where 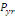 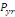 = acceptable annual risk of infection caused by a pathogenic
organism = acceptable annual risk of infection caused by a pathogenic
organism
n = number of exposure events per year (events/yr).
A QMRA model for broccoli, cucumber, lettuce, and three
cultivars of cabbage constructed by Hamilton et al. (2006) was used to
calculate the daily dose of pathogenic organism on the lettuce. The beta
-Poisson and exponential dose -response models were subsequently used to
calculate the probability of infection (Nana O.B. Ackerson and Esi Awuah,
2012).
The daily dose of pathogens, ë=d, taken as a result of
consuming the lettuce was calculated as:
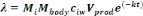 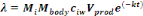 (Equation 8) (Equation 8)
Where,
Mbody = human body mass (kg)
Mi = daily consumption per capita per kg of body
mass [g (kg.ca.day)-1]
ciw= concentration of pathogens in irrigation
water
Vprod= volume of irrigation water caught by product
(mL.g-1)
k = pathogen kinetic decay constant (day-1)
t = time between last reclaimed - water irrigation event and
harvest/consumption/storage (day).
Mbody = 71.8 kg
From survey, Mi = 1.6713 g.
(kg.ca.day)-1
Vprod = 0.125 mL g-1 ; t = 2
d.
Table 4: Summary of
dose-response parameters for exponential and beta-Poisson models from various
enteric pathogen ingestion studies
|
Exponential
|
beta-Poisson
|
|
Constituent
|
r
|
á
|
â
|
N50
|
|
Escherichia coli
|
|
0.1705a
|
1.61 x 106a
|
|
|
Salmonella
|
0,00752a
|
0,313b
|
|
23600b
|
|
Ascaris
|
1b
|
0,104c
|
|
859c
|
a= (Metcalf & Eddy, 2007); b=
(Schönning et al., 2007); c= (Mara and Sleigh,
2010b)
| 


