La spectroscopie d'impédance électrochimique
est une méthode puissante de l'évaluation de la performance d'un
supercondensateur dans le domaine fréquentiel. Celle-ci permet de
caractériser les composants à stockage faradique et non-
faradique [71] à savoir : résistance de l'électrolyte,
capacité de la double couche, résistance de polarisation,
résistance de transfert de charge, élément à phase
constante (CPE), impédance de diffusion de charge, inductance virtuelle,
etc.
Avec cette technique, le supercondensateur peut être
caractérisé par ses différents éléments ; la
capacité et les diverses contributions de l'ESR peuvent être
déterminées séparément.
3.2.3.1. Définition et principe
Le principe de sp ectroscopie d'impédance
électrochimique est basé sur la mesure d'une fonction de
transfert suite à la perturbation imposée du système
électrochimique étudié. Couramment, la perturbation est
sinusoïdale. Le si gnal appliqué est donc de la forme suivante [72]
:
e ( t ) = E max
.sin(ù.t) 3-12
La réponse en courant parcourant le composant
électrochimique est de la même forme avec un déphasage
ö comme l'illustre l'équation suivante :
i ( t ) = I max .
sin(ù.t -?) 3-13
L'impédance électrochimique se définie
comme étant le nombre complexe Z(ù) résultant du
rapport :
E(ù)
Z=
( ) ù
3-14
I ( )
ù
où, en mode potentionstatique, E(ù) est
la perturbation imposée à un potentiel maximal
choisiEmax et I(ù) la réponse en courant du
composant étudié.
3.2.3.2. Essai de spectroscopie
d'impédance
õEn mode de caractérisation
potentiostatique, le supercondensateur est polarisé par une tension
continue U durant un certain temps avant le lancement des mesures de
l'impédance. La durée de cette polarisation est fixée
à une heure pour notre étude. Ce temps est certainement suffisant
pour charger tous les éléments du supercondensateur notamment
ceux de faibles accessibilités.
Un signal sinusoïdal de 10 m V (cette grandeur de
tension permet d'avoir un bon compromis entre la précision de mesure et
la perturbation électrochimique) est ensuite superposé à
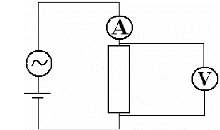
la tension stabilisée U. Le principe de spectroscop ie
d'impédance électrochimique est présenté sur la
figure 3-12. Les câbles de mesure et de puissance sont torsadés
afin de minimiser l'effet des perturbations électromagnétiques.
L'impédancemètre IM6+PP240 de Zahner est nécessaire pour
appliquer une faible tension alternative et mesurer l' évolution du
module et de la phase de l'impédance sur une plage de fréquences
[73]. Les caractéristiques techniques du spectromètre sont
détaillées dans l'annexe A.
Partie de puissance Partie de mesure

e(t)
U
Z
Fig. 3-12 : Schéma du principe de la
caractérisation par spectroscopie d'impédance
En variant la réponse du signal alternatif, nous
obtenons un spectre de l'impédance en fonction de la pulsation
ù. La plage de fréquence a été choisie
entre 10 mHz à 10 kHz, ce quipeut inclure la plupart des
applications du supercondensateur. L'impédance obtenue peut être
représentée sous plusieurs formes grâce aux tracés
de Bode ou de Nyquist.
L a figure 3-13 pré sente le diagramme de Bode pour le
supercondensateur BCAP010 mesurée à une tension continue de 2,5 V
et à une température ambiante de 25 °C. Cette
représentation permet de mettre en évidence l'existence de
certains paramètres du supercondensateur, tels que la résistance
ESR, la capacité C et l'inductance L.
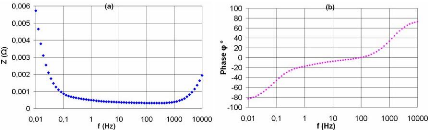
Fig. 3-13 : Module et phase de l'impédance du
supercondensateur BCAP010 en fonction de la fréquence
La figure 3-14 montre que la partie imaginaire de
l'impédance mesurée par spectroscopie d'impédance peut
être interprétée par deux zones (capacitive et inductive)
suivant le comportement fréquentiel du supercondensateur [74].
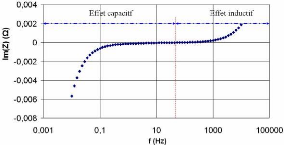
Fig. 3-14 : Partie imaginaire de l'impédance du
supercondensateur BCAP010
> Pour une fréquence supérieure à
celle de résonance (45 Hz pour le composant BCAP010), dit hautes
fréquences, nous rencontrons l'effet inductif due à l'inductance
propre du supercondensateur et à l'inductance parasite des câbles
de connections.
> Pour une fréquence inférieure à
celle de résonance (fréquences intermédiaires entre 55 mHz
et 45 Hz pour le composant BCAP010), c'est l'effet capacitif qui
prédomine, la capacité augmente avec la diminution de la
fréquence à cause de la nature poreuse des électrodes (cf.
fig. 3-15). Les électrodes sont fabriquées avec une surface
poreuse très élevée, les pores ayant un diamètre de
l'ordre du nanomètre.
> A basse fréquence (<10 mHz) la
réactance, principalement attribuable à la capacité, est
à son minimum. Dans ces conditions, les ions ont le temps de
pénétrer dans la profondeur des pores et la surface maximale de
l'électrode est utilisée pour contribuer à la
capacité de la double couche ( Cdl) [75].
La réactance Xc permet de
déterminer la capacité du composant comme le montre
l'équation 3-15.
1
C ù = -
( ) 3-15
c
ùX
La figure 3-15 illustre l'augmentation de la capacité
avec la décroissante de la fréquence, nous pouvons voir
qu'à très basse fréquence (55 mHz) la capacité
commence à se stabiliser à des valeurs comparables à
celles qui résultent de la méthode précédente de
charge/décharge.
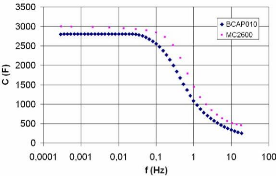
Fig. 3-15 : Evolution de la capacité des
supercondensateurs BCAP010 et M600 vis-à-vis de la
fréquence
> A très basse fréquence (<< 10 mHz),
les phénomènes lents tels que la redistribution de charges et
l'autodécharge dominent le comportement du supercondensateur. Des essais
expérimentaux permettant la détermination des
éléments propre ces phénomènes seront
décrits ultérieurement.
La spectroscopie d'impédance électrochimique
nous permet de connaître, les diverses
contributions résistives de l'ESR [26, 76]. Elles sont
mises en évidence sur la figure 3-16.
> La résistance série Rs
représente l'ensemble de la résistance de l'électrolyte,
des électrodes, des collecteurs de courant et du séparateur.
Cette résistance peut être déterminée à la
fréquence de résonance.
> La résistance de l'électrolyte dans les
pores est appelée résistance équivalente distribuée
EDR : elle intervient à plusieurs niveaux et est difficile
à évaluer. Elle est fonction du transfert ionique dans les pores
du matériau d'électrode, éventuellement à
l'interface électrolyte/électrode, des transferts
électroniques à l'interface électrode/collecteur de
courant, etc.
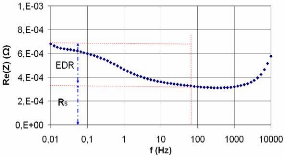
Fig. 3-16 : Contribution d'ESR du
supercondensateur
A basse fréquence tous les éléments
résistifs sont présents alors qu'à fréquence
élevée seule la résistance Rs
intervient.
Les erreurs de mesure pour un essai de spectroscopie
d'impédance peuvent être déterminées pour le module
et la phase. Sur la figure 3-17, nous montrons les erreurs faites en fonction
de la fréquence pour l'essai présenté. Nous observons que
ces erreurs sont variables suivant l'impédance mesurée.
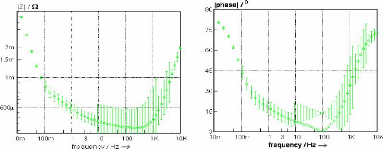
Fig. 3-17 : Erreurs de mesure provoquées par
spectroscopie d'impédance
3.2.3.3. Dépendance des paramètres du
supercondensateur avec la tension 3.2.3.3.1. Origine de la
non-linéarité de la capacité du
supercondensateur
La capacité est proportionnelle à la surface de
l'interface et proportionnelle à l'inverse de la distance entre les
charges. L'augmentation de la capacité due à l'augmentation de la
tension peut être expliquée par la réduction de la distance
entre les charges électrostatiques en raison de la compression
électrostatique. Cette variation est aussi due à la variation de
la constante diélectrique attribuable à l'électrostriction
ou à la variation de la surface accessible [65, 77].
3.2.3.3.2. Plan de mesure
La spectroscopie d' impédance permet, comme
énoncé auparavant, de caractériser les paramètres
du supercondensateur pour une tension de polarisation donnée.
Nous avons caractérisé le supercondensateur BCAP010
à une température de 25 °C pour une tension de 0 à
UN en suivant les étapes suivantes (illustration faite sur la
figure 3-18) :
· court-circuit du supercondensateur pendant 24 h,
· court-circuit deux heures avant chaque mesure pour une
tension donnée,
· chargement pendant une heure à une tension
constante avant le lancement de la mesure,
· mesure de l'impédance (environ 30 minutes),
· court-circuit deux heures avant la mesure suivante,
etc.
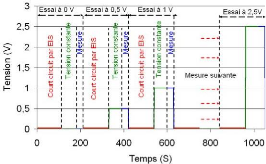
Fig. 3-18 : Protocole de mesure de l'impédance du
supercondensateur en fonction de la tension
Ce plan de caractérisation a été choisi
pour pouvoir caractériser le supercondensateur avec pratiquement le
même état initial quelque soit la tension. Nous présentons
sur la figure 3-19 le tracé de Nyquist du supercondensateur BCAP010
obtenu pour l'intervalle de fréquence de 10 mHz à 10 kHz et pour
des tensions de polarisation de 0 ; 0,5 ; 1 ; 1,5 ; 2 et 2,5 V.
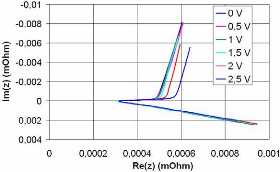
Fig. 3-19 : Tracé de Nyquist du supercondensateur
pour un intervalle de tension [0 ; 2,5] V
A partir des résultats montrés sur la figure
3-20, nous pouvons observer que la capacité de la double couche du
supercondensateur dépend fortement de la tension appliquée
à ses bornes. Ceci est observé à partir des
fréquences inférieures à 1 Hz et surtout pour des tensions
supérieur à 0,5 V.
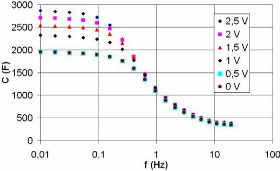
Fig. 3-20 : Evolution de la capacité du
supercondensateur BCAP010 en fonction de la fréquence et de la tension
à ses bornes
Nous montrons sur la figure 3-21 l'évolution de la
partie réelle de l'impédance du supercondensateur en fonction de
la tension et de la fréquence. La résistance du supercondensateur
en haute fréquence est indépendante de la tension
appliquée. Elle commence à s'accroître faiblement avec
l'augmentation de la tension en dessous de la fréquence de
résonance.
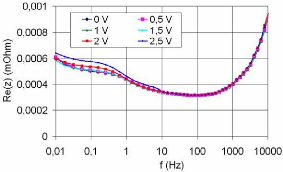
Fig. 3-21 : Évolution de l'ESR du
supercondensateur en fonction de la tension et de fréquence
La dépendance de la capacité du
supercondensateur C avec la tension U est montrée sur
la figure 3-22 pour une fréquence de 10 mHz. La résistance
Rs déterminée à la fréquence de
résonance est invariable en fonction de la tension. En revanche, la
résistance que présente la résistance de
l'électrolyte EDR augmente avec l'augmentation de la tension.
La figure 3-22 montre la variation de l'EDR déterminée pour une
fréquence de 55 mHz en fonction de la tension. Cette dernière est
l'image de la résistance de l'électrolyte distribuée
liée au phénomène de diffusion sans tenir compte de celle
liée au phénomène de redistribution de charge.
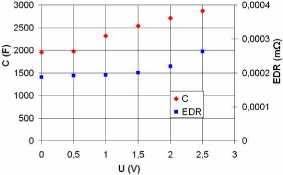
Fig. 3-22 : Évolution de la capacité et de
l'EDR du supercondensateur en fonction de la tension
Dans la suite de ce rapport les deux fréquences de 10
mHz pour la capacité et de 55 mHz pour l'EDR sont
considérées pour étudier la dépendance thermique,
potentielle, etc. du supercondensateur.
3.2.3.3.3. Effet du protocole de caractérisation
sur les paramètres du supercondensateur Nous avons
proposé dans le paragraphe précèdent un protocole de
caractérisation du spectre
d'impédance du supercondensateur pour
différentes tensions. Nous proposons dans ce paragraphe un autre plan de
mesure de l'impédance afin d'une part d'étudier l'influence de la
méthode du chargement du supercondensateur sur ses paramètres et
d'autre part, de simplifier la caractérisation du spectre
d'impédance, qui était relativement longue auparavant.
Nous présentons sur la figure 3-23 le nouveau
protocole de caractérisation par spectroscopie d'impédance. Dans
ce nouveau plan, nous avons supprimé le temps du court-circuit
effectué entre deux mesures.
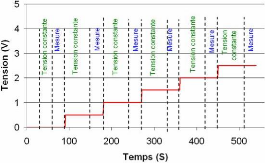
Fig. 3-23 : Deuxième protocole de mesure de
l'impédance
du supercondensateur en fonction de la
tension
Les résultats obtenus par le deuxième protocole
sont comparés avec ceux du premier protocole (cf. fig. 3-24). Nous
montrons sur cette figure la capacité déterminée à
10 mHz et 25 °C. Les valeurs de la capacité
déterminées par les deux protocoles sont proches.
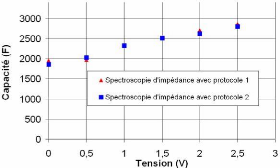
Fig. 3-24 : Evolution de la capacité du
supercondensateur BCAP010
vis-à-vis de la tension
déterminée par deux protocoles différents
Nous comparons sur la figure 3-25 la variation de la
résistance EDR en fonction de la tension. Contrairement aux
résultats précédents, nous trouvons qu'il y a un petit
écart entre les
valeurs de l'EDR obtenues par les deux protocoles pour des
tensions supérieures à 1 V. La caractérisation par le
deuxième protocole conduit à accumuler des charges dans les pores
du supercondensateur au fur et à mesure et donc la résistance
EDR diminue.
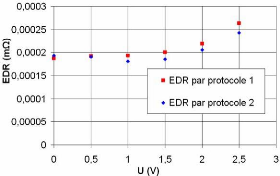
Fig. 3-25 : Evolution de la capacité du
supercondensateur BCAP010
vis-à-vis de la tension
déterminée par deux protocoles différents
3.2.3.4. Capacité des supercondensateurs
étudiés
Pour terminer, nous présentons sur la figure 3-26
l'évolution de la capacité des supercondensateurs
déterminée par le deuxième protocole à 25 °C
et pour une fréquence de 10 mHz. Ces résultats confirment la
dépendance de la capacité des supercondensateurs sur la tension
et que la relation n'est pas exactement une droite.
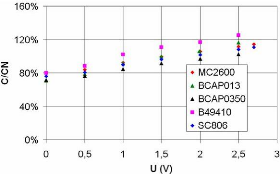
Fig. 3-26 : Evolution de la capacité des
supercondensateurs étudiés en fonction de la tension



