Etude et modelisation des supercondensateurs

3.3.3. Modélisation temporelle du supercondensateur : modèle à deux

branches

Nous avons trouvé qu'un simple circuit équivalent RC ne suffit pas à caractériser le comportement des supercondensateurs compte tenu de phénomènes qui comptent beaucoup dans leur comportement tels que la non-linéarité de la capacité de la double couche, la

redistribution de charge, etc. Nous avons donc besoin d'un modèle complet, qui prend en compte les différents phénomènes particuliers des supercondensateurs avec simplicité. Dans la suite, nous présenterons un modèle qui répond à ces questions tel que celui établi par Zubieta et al. [41, 81-83]. Ce modèle repose sur la répartition de l'énergie électrostatique des supercondensateurs en deux : une énergie rapidement stockée et une énergie lentement stockée.

3.3.3.1. Non-linéarité de la capacité de la double couche du supercondensateur

L'étude de la physique de la double couche montre que la capacité de la double couche n'est pas une constante, mais dépend fortement de la tension appliquée aux bornes du supercondensateur. Dans le paragraphe 3.2.2, l'étude expérimentale par le cycle de voltampérométrie a mis en évidence cette dépendance. Une modélisation de cette propriété est donc nécessaire afin d'obtenir des résultats précis lors de la simulation. Sur la base de la physique de la double couche, la capacité différentielle peut être modélisée en première approximation par une capacité d'une valeur constante C0 et une capacité dont la valeur varie de manière linéaire (k.u) en fonction de la tension u à ses bornes comme indiqué dans l'équation ci-dessous [41,82] :

Cdiff ( u) = C₀ + k.u 3-16

3.3.3.2. Circuit équivalent

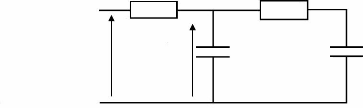
Le circuit équivalent du supercondensateur, dit modèle à deux branches, est composé de deux cellules RC : une branche rapide _R1C1, qui intervient dans le régime transitoire, et une branche lente _R2, qui représente la redistribution des charges (cf. fig.3-31). Afin de tenir compte de la non-linéarité de la capacité du supercondensateur, la capacité de la branche rapide C1 est choisie variable en fonction de la tension à ses bornes (cf. eq. 3-17).

R1 R2

u

u 1

C1 C2

Fig. 3-31 : Modèle à deux branches du supercondensateur [41, 82]

C₁ ( u ₁) = C0+k.u 1 3-17

La propriété de la non-linéarité de la capacité de la double couche a pour conséquence que l'énergie stockée dans le supercondensateur est plus importante que dans le cas d'une capacité constante C0. La forme de l'énergie peut être écrite comme suit [41, 82] :

C k

0 3

W = u +

2

. . u 3-18

1 1

2 3

3.3.3.3. Identification des paramètres de la branche rapide

La méthode de caractérisation des éléments du circuit équivalent consiste à charger le supercondensateur par un courant constant d'une valeur élevée jusqu'à la tension nominale, et ensuite de laisser le supercondensateur en circuit-ouvert un certain temps. La procédure d'identification est basée sur l'hypothèse simplificatrice que les phénomènes rapides et lents se succèdent (rapide ensuite lent). Celle-ci doit s'opérer à courant élevé dont l'ordre de grandeur est celui du courant nominal du supercondensateur. Pour un seul cycle l'effet de l'autoéchauffement qui sera montré ultérieurement a une influence faible et négligeable sur la caractérisation par courant constant.

Vu que les deux branches possèdent des constantes de temps largement distinctes (R2C2

>> R

1 1 C ), pendant la phase de charge, la branche lente reste quasiment inactive. Le circuit

équivalent sera donc réduit comme suit :

I R1

u

C1

		u1

Fig. 3-32 : Circuit équivalent de la branche rapide

La résistance du supercondensateur R1 est déterminée par la formule présentée par l'équation 3-2.

Identification de la capacité C0

La capacité con stante C0 dans l'équation 3-17 peut être déterminée à partir de la définition de

la capacité différentielle à l'état initiale de la charge comme suit :

dq

I dt I

C0 = = = 3-19

du

(0) (0) (0) /

du du dt

avec,

q la charge stockée dans le supercondensateur.

Le rampe du(0)/dt est mesuré au voisinage de l'instant initial comme le montre la figure 3-33.

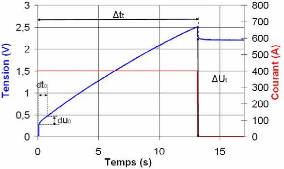
Fig. 3-33 : Principe de l'identification des éléments de la branche rapide

Identification de la constante k

L 'expression de la charge totale Qt stockée dans le supercondensateur à la fin de la charge en fonction de la durée totale Ätt de la charge et du courant de la charge I peut être donnée par l'équation ci-dessous :

Q t = I Ät t 3-20

Avec ÄUt l'évolution totale de la tension aux bornes du supercondensateur, nous pouvons obtenir la charge totale :

1

Q t = C Ä U _t + k Ä U t 3-21

2

0 2

A partir des deux expressions précédentes (3-20) et (3-21) nous pouvons écrire :

2 ( I. t - C · U )

Ä t 0 Ä t 3-22

ÄU t

k = 2

3.3.3.4. Identification des paramètres de la branche lente

Lorsque la tension aux bornes du supercondensateur atteint sa valeur nominale, le courant

d'alimentation s'annule et le phénomène prédominant dans le composant est celui de la redistribution de la charge entre les branches ra ide et lente. Le circuit équivalent schématisé

p

sur la figure 3-34 représente le supercondensateur durant cette phase oü R2 et C2 sont les éléments de la branche lente.

R2

I

C1

u2

u1

C2

Fig. 3-34 : Modèle équivalent durant la phase de redistribution

Identification de R2

Au moment de l'annulation du courant d'alimentation, le courant (initial) parcourant l'élément C2 est considéré nul, ce qui permet d'écrire l'équation suivante :

I (0) = Udébut / R₂ 3-23

De plus, la relation entre le courant de la capacité C1 et la tension à ses bornes à ce momentci peut être donnée par la formule suivante :

du

I = - C

(0) 1 (0) 3-24

1 dt

Pour le calcul de R2, nous approximons la pente initiale observée sur la tension du supercondensateur par une quantité ÄU/Ät, comme l'illustre la figure 3-35 et nous évaluons le terme I(0) pour le niveau médian de tension, à savoir _Udébut-ÄU /2 [4].

Ainsi R s'exprime par :

2

3-25

U - Ä U / 2 début Ät

C Ä U

1

R=
2

oü, _Udébut est la tension au début de la phase de redistribution.

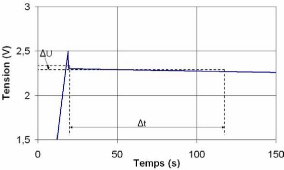
Udébut

Fig. 3-35 : Evolution de la tension aux bornes du supercondensateur pendant la phase de redistribution

Identification de la capacité C2 :

La capacité C2 peut être calculée à la fin de cette période oil les tensions sur C1 et C2 sont

supposées égales à la même valeur Ufi_n. En appliquant l'équation de conservation de la charge sur la charge stockée au début et à la fin de la phase de redistribution, nous pouvons écrire l'équation suivante :

C1 . U début = C ₂.U Cl + 3-26

fin fin

soit,

C2 = C1 . ( U début - U fin) / U fin 3-27

oil Ufi_n est la tension à la fin de la phase de redistribution.

Ce phénomène de redistribution interne, auquel sont associées des constantes de temps généralement très longues, met bien en évidence le problème de la disponibilité de l'énergie stockée dans les supercondensateurs. La majeure partie de celle-ci peut, certes, être qualifiée de rapide mais il reste une partie considérablement liée aux phénomènes lents [5,43].

Dans le tableau 3-2, nous donnons les valeurs des éléments du modèle à deux branches pour le supercondensateur BCAP010 déterminés à courant de charge de 400 A et à une température de 25 °C.

C1		R1 (u?)	C2 (F)		R2 (?)	C0 (F)
k (F/V)					1882
523	447	172	1,92

Tab. 3-2 : Eléments du modèle à deux branches pour le supercondensateur BACAP010 à 25 °C

3.3.3.5. Effet du courant de la charge/décharge

Afin de montrer l'influence du courant de charge/décharge sur la caractéristique électrique du supercondensateur, nous avons réalisé un essai de charge/décharge avec cinq courants différents 50, 100, 200, 300, et 400 A pour le supercondensateur BCAP010 à 25 °C. Le tableau 3-3 présente les résultats expérimentaux des éléments de la capacité C1 (C0 et k) et la résistance R1 déterminées au début de la charge et de la décharge. Nous trouvons que le choix de la valeur du courant de charge a une influence assez importante sur les résultats obtenus par cette technique : la capacité C1 calculée à la tension nominale varie de #177;4% et la résistance R1 de - 6% à +2% par rapport à leurs valeurs moyennes.

Courant (A)		k (F/V)	C0 (F)	C1 (F) à 2,5 V		R1 (u?)	400
Charge	523,2	1882	3190	447
	408	2165	3185	422		300
Charge	540	1832	3182	450
	431	2120	3178	420		200
Charge	550	1850	3225	450
	427	2084	3152	430		100
Charge	556	1857	3247	440
	414	2048	3083	450		50
Charge	595	1838	3326	410
	395	2075	3063	440		Moyenne
			3192	436

Tab. 3-3 : Éléments de la branche rapide déterminée à différents courant de charge/décharge

Sur la figure 3-36, nous représentons les résultats obtenus de la capacité C1 en tension nominale. D'après cette figure, nous observons que la capacité C1 déterminée durant la charge augmente avec la diminution du courant, tandis qu'elle diminue durant la décharge. La différence entre la capacité de charge et de décharge s'accroît donc avec la diminution du courant de charge.

L'écart existant entre la capacité de charge et de décharge a déjà été évoqué dans le paragraphe 3.2.2 qui traite de la méthode voltampérométrie ; la capacité de la charge est toujours supérieure à celle de la décharge.

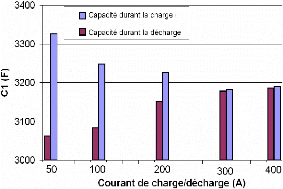
Fig. 3-36 : Capacité du supercondensateur BCAP010 déterminée à des différents courants de charge

Sur la figure 3-37, nous présentons le rendement oulombien vis-à-vis

c du courant de la

charge/décharge. No const

us atons ue l

q e rendement coulombien augmente avec

l'augmentation du courant de charge. Lors de la charge d'un supercondensateur par un faible courant les capacités liées aux phénomènes lents corre

sont ctement chargées, mais ces mêmes

capacités ne sont pas déchargée s pendan la dé arge l (à faib urant), car leurs charges

t ch ente le co

sont alors piégées dans les pores étroits.

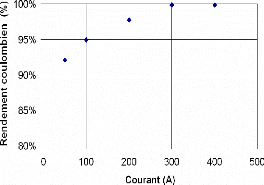
Fig. 3-37 : Rendement coulombien vis-à-vis du courant de charge/décharge

3.3.3.6. Comparaison du rendement coulombien des supercondensateurs étudiés

Dans le tableau ci-dessous, nous présentons les paramètres principaux R1 et C1 et le rendement coulombien pour des composants de différents fabricants MAXWELL, BATSCAP et EPCOS. Ces paramètres sont déterminés avec une valeur de courant de charge/décharge par Farad constante (0,15 A/F) pour les composants BCAP010, BCAP013, M600, et SC806.

Pour le composant B49410, cette valeur est de 0,11 A/F car la valeur nominale du courant de 540 A est supérieure à celle fournie par notre banc de manipulation. Pour le composant BCAP0350 cette valeur est de 0,09 A/F à cause de son faible courant nominal.

Nous trouvons d'après ces résultats que le rendement coulombien varie suivant le composant. Ce paramètre donne des informations importantes sur le niveau des phénomènes faradiques dans les supercondensateurs.

	Numéro de série	CN (F)	UN (V)	I (A)	I/CN (A/F)		R1 (m?)	k (F/V)	C0 (F)	C1 (UN) (F)		ç, (%)	MAXWELL
BCAP0350	350	2,5	30	0,09	Charge	4,3	57	239	389	96
						3,3	45	260	373
	450	2,5	70	0,15	Charge	2,120	113	309	590	97
						1,685	93	338	571
SC806	2600	2,7	400	0,15	Charge	0,912	551	2025	3512	81*
						0,462	324	1964	2840
B49410	3600	2,5	400	0,11	Charge	0,210	1065	2649	5311	96
						0,210	850	2997	5122
BCAP010	2600	2,5	400	0,15	Charge	0,447	523	1882	3190	100
						0,422	408	2165	3185
	2600	2,7	400	0,15	Charge	0,360	546	2024	3390	95
						0,317	321	2407	3210

Tab. 3-4 : Paramètres des supercondensateurs de différents fabricants

* Cette faible valeur n'a été mesurée que sur un élément BATSCAP. Elle serait à confirmer sur
d'autres éléments de ce même fabricant.

3.3.3.7. Comparaison des résultats obtenus par différentes méthodes

3.3.3.7.1. Présentation de la non-linéarité de la capacité obtenue par les différentes techniques

Nous nous intéressons à comparer les résultats obtenus temporellement par charge/décharge

à courant constant (procédure de Zubieta [41]) avec ceux obtenus par voltampérométrie et ceux donnés par spectroscopie d'impédance (à une température de 25 °C) (cf. fig. 3-38). Nous présentons sur cette figure les résultats de la mesure de la capacité du supercondensateur en fonction de la tension.

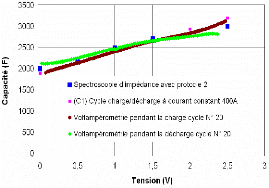
Fig. 3-38 : Comparaison des mé thodes tér on par la mesure

de carac isati

de la capacité en c

fon tion de la nsion

te

Les différentes techniques donnent des résul t ats diffé rents.

> Pendant la charge : les valeurs de la capacité m esurée par les méthodes temporelles (c harge/d éc harge à c o ura n t con s tant et voltampérométrie) sont assez proches. Celles obtenues par spectrométrie d'impédance sontinférieures à celles obtenu es par les méthodes temporelles.

> Pendant la écharge es v leurs e la cap cité o tenu s par ltamp

d l a d a b e vo erométrie

sont pratiquement identiques à celles obt enues par spec tr osco p ie d' im pédance, mais différentes de celles obtenues par charge/décharge à courant constant.

3.3.3.7.2. Comparaison de la capacité nominale obtenue par différentes techniques

Nous avons vu précédemment (cf. § 3.2.1) qu'il existe différentes méthodes permettant de déterminer la capacité du supercondensateur. Ces méthodes déterminent la capacité en supposant que celle-ci est indépendante de la tension appliquée dans l'intervalle de tension [UN/2 ; UN]. La détermination de cette capacité, dite capacité nominale, peut être réalisée par d'autres techniques en calculant la moyenne des capacités dans l'intervalle de tension mentionnée ci-dessus [84].

Nous comparons dans le tableau 3-5 la valeur de ces capacités à celle donnée par le fabricant pour les deux supercondensateurs BCAP010 et M600. Nous observons, comme prévu, que cette valeur obtenue par spectroscopie d'impédance et par voltampérométrie (décharge à 20 cycles) est très proche de celle de la méthode normalisée et de celle de MAXWELL, tandis que la méthode à charge/décharge à courant constant (C1) et par voltampérométrie (charge à 20 cycles) donnent des valeurs élevées.

	Capacite (F)	Courant constant (C1)		EIS à 10 mHz	Voltampérométrie (20 cycles)		Méthode norme IEC 6239			Méthode MAXWELL 400 A
		Décharge à 50 A			Décharge	400 A	50 A
	2600	2600	2600	2600	2600	2600	2600		2600	BCAP010
C	2863	2816	2614	2792	2596	2750	2623		2645
	110%	108%	101%	107%	100%	106%	101%		102%	M600
C	3130	-	2842	2956	2869	2857	2861		2902
	120	-	109	114	110	110	110		112

Tab. 3-5 : Détermination expérimentale de la capacité nominale
des supercondensateurs BCAP010 et M00

3.3.3.7.3. Comparaison des résistances par différentes techniques

Nous comparons dans le tableau 3-6 les valeurs de la résistance ESR obtenues par différentes méthodes de caractérisation à 25 °C et pour les deux supercondensateurs BCAP010 et M600.

Nous pouvons distinguer dans la documentation du fabricant comme MAXWELL deux résistances : la résistance DC (déterminée par décharge à courant constant) et la résistance AC (déterminée par une fréquence donnée). Nous présentons dans le tableau les valeurs réduites par rapport aux résistances DC et AC.

Nous pouvons constater que les valeurs de la résistance sont dispersées chaque méthode donnant une valeur différente des autres, mais les mesures par la méthode de MAXWELL, par la norme IEC 6239 et par spectroscopie d'impédance (à basse fréquence) donnent de s valeurs proches.

	Resistance (An)	EIS		Norme IEC 6239		MAXWELL à 400 A		Courant constant à 400 A
		ESR (55mHz;UN)	400 A	50 A
ESR	322	620	587	792	508	447
	700	700	700	700	700	700
	46	89	84	113	73	64
	300	300	300	300	300	300
	107	201	196	264	169	149		M600
ESR	272	439	422	701	405	360
	400	400	400	400	400	400
	69	110	106	175	101	90
	280	280	280	280	280	280
	97	157	150	250	145	129

Tab. 3-6 : Comparaison des valeurs de résistance obtenues par différentes méthodes

3.3.3.8. Validation expérimentale et limitation

Pour vérifier que le modèle à deux b ch

ran es étudié est précis, nous avons simulé ce modèle

grâce au log l S

icie implore ous p entons sur la figure 3-39, o

r. N rés la c mparaison du résultat de

simulation avec la réponse expérimentale. Cette figur ontre

e m d'une manière générale que le

modèle à d x ches sente c une nne p ision compo ement trique

eu bran repré ave bo réc le rt élec du
supercondensateu

r.

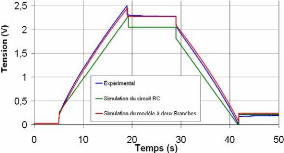
Fig. 3-39 : Comparaison du modèle à deux branches avec un essai expérimental

Cependant, un petit écart apparaît entre les résultats simulés et expérimental en fin de la charge, au début de la phase de redistribution et lors de la décharge (cf. fig. 3-40). Ceci résulte de la nature distribuée de la résistance et de la capacité du supercondensateur dûe à la structure poreuse des électrodes de structure volumique. L'effet de cette dernière peut être observé sur la courbe de charge/décharge et surtout après l'annulation du courant de charge/décharge (cf. fig. 3-40-a). De plus, la variation des éléments de la branche rapide de ce modèle en fonction du courant de la charge ou de la décharge n' st pas prise e

e n compte.

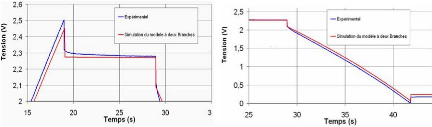
(a)

(b)

Fig. 3-40 : Présentation de l'écart entre le mo dèle à b

deux ranch l'ess

es et ai expérimental

Pour confirmer les résultats obtenus ci-dessus, nous avons réalisé un essai fréquentiel à 25 °C et à une tension de polarisation de 2,5 V sur le supercondensateur BCAP010. Nous

comparons sur la figure 3-41 le tracé de Nyquist du modèle à deux branches avec celui expérimental. Nous pouvons constater à partir de cette figure que la résistance R1 est supérieure à R_s. Par conséquent, pour la raison mentionnée ci-dessus le modèle à deux branches est limité et ne peut donc constituer un bon modèle dynamique du supercondensateur.

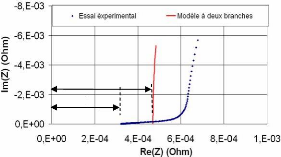
R_s

R1

Fig. 3-41 : Comparaison de la réponse en fréquence du modèle à deux branches avec l'essai fréquentiel

D'autres modèles temporels tels que celui proposé dans la référence [42] s ont présentés dans la littérature, mais le calcul complexe des éléments du modèle ainsi que le temps de simulation lent limite considérablement l'utilisation de ce type de modèle [85, 86].