S'il existe des contacts électrode
positive-électrode négative, l'autodécharge prendra place
sous la forme d'un effet de couple galvanique [137].
La décroissance de la tension aux bornes d'un
supercondensateur chargé et déconnecté illustre, durant
une période de temps prolongé, l'existence d'un courant
If, appelé courant de fuite. Pour tenir compte de
l'autodécharge due au courant de fuite dans la modélisation d'un
supercondensateur, il est courant d'ajouter au circuit équivalent une
résistance de fuite Rf en parallèle avec la
capacité totale du supercondensateur (cf. fig. 4-3) [144]. La valeur de
ce courant de fuite dépend essentiellement de la concentration des
impuretés et de l'épaisseur de la membrane poreuse [62].
R1 R2
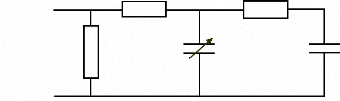
Rf
C1
C2
Fig. 4-3 : Circuit équivalent du
supercondensateur
(développé à partir du modèle
de Zubieta) tenant compte du courant de fuite
Dans ce cas, la décroissance de la tension aux bornes du
supercondensateur peut être modélisée sous forme d'une
fonction exponentielle comme dans l'équation suivante :
?? - t ???
exp 4-2
0 ? ? ô f ?
u ( t ) U
=
où,
U0 est la tension initiale aux bornes du
supercondensateur en circuit ouvert au moment de
l'arrêt du courant de charge, t est le temps
écoulé, ôf est la constante de temps
représentant le courant de fuite.
Nous tenons à signaler que ôf est
simple à déterminer, puisqu'il suffit d'approximer la
décroissance du potentiel du supercondensateur par une exponentielle
comme le montre la figure 4-4.
La constante de temps ô et la capacité
du supercondensateur C sont utilisées pour calculer la
f 1
résistance de fuite Rf par la formule 4-3. La
capacité totale du supercondensateur peut être
représentée seulement par la capacité C1, car
l'effet du phénomène de la redistribution est relativement faible
dans ce cas.
ô f
R = 4-3
1 ( U 0
fC )
Par exemple, pour le composant BCAP010, Rf =1,34 k?.
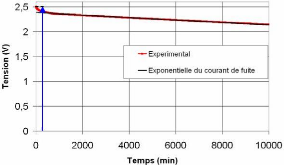
U0
Fig. 4-4 : Exponentielle représentative du
courant de fuite
par rapport à la courbe expérimentale pour le
composant BCAP010
Le circuit équivalent schématisé sur la
figure 4-3 ainsi que les paramètres du supercondensateur BCAP010 ont
été implantés dans le logiciel Simplorer. La comparaison
des résultats de la simulation avec un essai expérimental,
montrée sur la figure 4-5, illustre une
erreur importante due à la représentation de
l'autodécharge par une simple résistance Rf. En
conséquence, les mécanismes de l'autodécharge ne peuvent
pas être complètement modélisés par une seule
résistance Rf en parallèle avec la capacité
C1. En effet, les deux mécanismes de l'autodécharge sont
couplés, notamment au cours des premières heures oü le
processus de diffusion lié à l'oxydoréduction gouverne
fortement l'autodécharge [138].
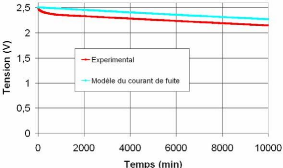
Fig. 4-5 : Comparaison du modèle de courant de
fuite avec un essai expérimental



