Etude et modelisation des supercondensateurs

4.4.2. Modèles prenant en c ompte l'autodécharge due au processus de

diffusion lié à l'oxydoréduction

4. 4.2.1. Modèle analytique

Nous avons constaté auparavant que la décroissance de la tension du supercondensateur pendant l'autodécharge n'est pas uniquement liée au courant de fuite, mais aussi au processus de diffusion lié à l'oxydoréduction. Ce dernier contrôle l'autodécharge durant les premières heures (de quelques heures à quelques dizaines d'heures) [116].

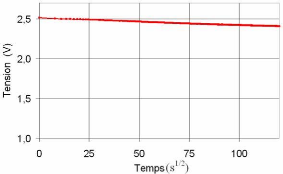
Fig. 4-6 : Courbe expérimentale de l'autodécharge tracée en fonction de
la racine carrée du temps pour le composant BCAP010

Pendant cette phase d'autodécharge du supercondensateur, la diminution de la tension du supercondensateur peut être modélisée moyennant certaines hypothèses simplificatrices par une équation fonction de la tension initiale et de la racine carrée du temps (cf. eq. 4-4 et fig. 4- 6) [138] :

u t U 0 - m t

( ) 4-4

où,

m est le paramètre de diffusion, qui peut être calculée par l'équation 4-5 :

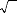
C q D

m R 0

= 4-5

C1 2

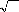
D est le coefficient de diffusion des ions dans l'électrolyte,

C12 est la capacité surfacique des deux doubles couches (positive et négative) du supercondensateur,

CR0 est la concentration initiale des espèces ioniques à l'interface électrode - électrolyte, q est la charge portée à la surface du charbon par ion.

Par exemple, pour le composant BCAP010 m = 7 mV/ s^1/2.

L'équation 4-4 décrit l'autodécharge du processus de diffusion lié à l'oxydoréduction pendant les premières heures, où le courant de fuite est faible et peut être négligeable [144]. La simulation complète de l'autodécharge consiste à associer les deux modèles : le modèle de courant de fuite et le modèle analytique de l'autodécharge due au processus de diffusion lié à l'oxydoréduction. Comme le montre la figure 4-7, il existe une faible erreur entre les résultats expérimentaux et la simulation. En effet, ce modèle est capable de modéliser parfaitement l'évolution de l'autodécharge du processus de diffusion lié à l'oxydoréduction avec le temps (erreur relative moyenne de 0,3%). Cependant, la difficulté de la construction du modèle est que les paramètres physiques requis pour calculer le paramètre de diffusion m, notamment CR0, sont difficile à déterminer. Par ailleurs, ce modèle ne peut pas être représenté par un circuit électrique équivalent.

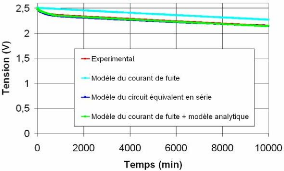
Fig. 4-7 : Comparaison du modèl analytique avec l'expérimental

e

4.4.2.2. Circuit série

Puisque le modèle analytique est difficile à ablir et limité par la quantité d'impuretés, un

ét

autre modèle est utilisable. Il se présente par deux circuit s RC en série modélisant les deux phénomènes de l'autodécharge (cf. fig. 4-8) [145]. La capacité totale du supercondensateur C1 est divisée en deux c apacités en série _Cfs ^et Crs.

u

R1

		Rfs		uf
	Rrs	ur

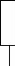
Cfs

R2

Crs C2

Fig. 4-8 : Circuit électrique équivalent du supercondensateur
prenant en compte l'autodécharge ; le courant de fuite par _Rfs ^et Cfs,
l'autodécharge du processus de diffusion lié à l'oxydoréduction par _Rrs ^et Crs

Pour identifier les nouveaux éléments du circuit électrique Rfs, Rrs, Cfs ^et _Crs, nous supposons que la courbe de la décroissance de la tension du supercondensateur u(t) est composée de deux exponentielles superposées avec deux constantes du temps différentes (cf. éq. 4-6). La première uf(t) représente l'autodécharge du courant de fuite et la deuxième u_r(t) (r pour redox) représente l'autodécharge du processus de diffusion lié à l'oxydoréduction. Cette dernière peut être déterminée par la différence de la courbe expérimentale de l'autodécharge avec

l'exponentielle liée au courant de fuite (cf. fig.4-9). Nous pouvons donc écrire :

u t u

( ) ( ) ( )

= t u t

+

f r

- t t 4-6

-

u t

( )

Ue

f 0

ô f + U_r 0 e ô_r

où,

Uf0 est la tension initiale de l'autodécharge du courant de fuite,

Ur0 est la tension initiale de l'autodécharge du processus de diffusion lié à l'oxydoréduction. Les deux tensions initiales sont déterminées à partir des résultats expérimentaux, comme illustré sur les figures 4-9.

ô_r est la constante de temps de l'exponentielle représentant l'autodécharge du processus de diffusion lié à l'oxydoréduction, elle est déterminée à partir des résultats expérimentaux. Le calcul de la deuxième constante de temps ôf est déjà présenté dans le paragraphe 4.4.1.

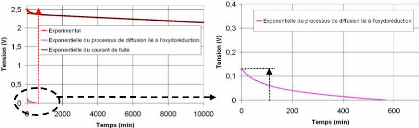
Uf0

Ur0

Fig. 4-9 : Courbe des exponentielles du courant de fuite et de
l'autodécharge du processus de diffusion lié à l'oxydoréduction

L'identification des deux capacités _Cfs ^et _Crs est basée sur l'hypothèse simplificatrice suivante : pendant la charge du supercondensateur le circuit électrique équivalent schématisé sur la figure 4-8 peut être réduit à deux condensateurs en série _Cfs ^et _Crs avec la résistance R1 (c f. fig. 4-10). Cette simplification est possible car les autres branches du circuit ont une constante de temps très élevé par rapport à celle de ce circuit. Ceci permet d'appliquer la loi de conservation de la charge : la charge totale stockée dans deux condensateurs en série est égale à la charge stockée dans chacun.

u

R

1

Cfs

Crs

uf ur

Fig. 4-10 : Circuit équivalent du supercondensateur pendant la charge

Ceci nous permet d'écrire l'équation suivante :

U 0

C = C 4-7

fs 1 U f 0

avec C1, capacité totale (équivalent à _Cfs en série avec Crs)

Ainsi, la valeur de la résistance de fuite peut être calculée par la relation ci-dessous :

ô f

R = 4-8

fs C

fs

Les paramètres de l'autodécharge du processus de diffusion lié à l'oxydoréduction sont calculés par la même méthode comme le montre les équations suivantes :

U₀

C = C 4-9

rs 1 U r 0

ô r

R = 4-10

rs C

rs

Dans le tableau ci-dessous nous présentons les valeurs des éléments du circuit série de l'autodécharge pour le supercondensateur BCAP010.

Cfs (kF)	Crs (kF)	Rfs (k?)		Rrs (?)	3,41
50	1,16	0,21

Tab. 4-1 : Eléments du circuit série de l'autodécharge du supercondensateur BCAP010

La comparaison des résultats expérimentaux avec la simulation est illustrée par la figure cidessous (cf. fig. 4-11). Nous constatons qu'il existe qu'une très légère différence entre la simulation du circuit série et la courbe expérimentale (erreur relative moyenne de 1,5%). La modélisation de l'autodécharge par un circuit électrique améliore nettement la simulation de l'autodécharge par rapport au modèle du courant de fuite. Cependant, l'erreur est légèrement supérieure à celle trouvée avec le modèle analytique notamment pendant les premières heures de l'autodécharge.

Le circuit série est un concept simple et assez facile à mettre en place par rapport au modèle analytique. Son intégration dans un logiciel de circuit électrique est aisée. Cependant, à partir du tableau 4-1, nous observons que les capacités _Cfs ^et _Crs possèdent des valeurs très élevées non représentatives du fonctionnement physique du composant.

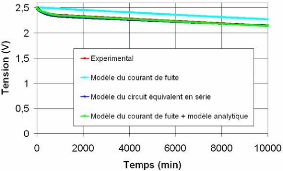
Fig. 4-11 : Comparaison du modèle du circuit série avec un essai expérimental

4.4.2.3. Circuit parallèle

Nous avons montré précédemment que la représentation de l'autodécharge par un circuit série engendre des valeurs élevées non représentatives des deux capacités _Cfs ^et Crs.

Établir un nouveau modèle de l'autodécharge représentant mieux les mécanismes physiques qu'elle engendre est donc souhaitable.

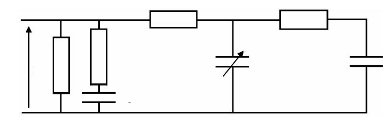
Nous proposons de modéliser l'autodécharge par une résistance Rf en parallèle avec la capacité totale du superc ondensateur C1 pour le courant de fuite intrinsèque à celle-ci et une capacité _Crp en série avec une rési stance R _rp pour l'autodécharge due au processus de diffusion lié à l'oxydoréduction, comme schématisé sur la figure 4-12. Ce circuit n'est qu'une extension de celui montré sur la figure 4-3 en ajoutant une branche _RrpCrp. De ce fait, la résistance de fu e Rf peut être calculée comme montré dans le paragraphe 4.4.1. Ainsi sa valeur reste

it

inchangée.

u

Rf

Rrp

Crp

R1 R2

C1 C2

Fig. 4-12 : Circuit équivalent du supercondensateur avec le circuit parallèle de l'autodécharge

Pour identifier les deux nouveaux éléments _Rrp ^et _Crp du circuit, nous simplifions le circuit équivalent ci-dessus à partir du comportement temporel du supercondensateur durant l'autodécharge :

· A l'instant zéro, au moment de l'arrêt du courant de charge, le circuit peut être simplifié par le schéma suivant :

U0

C1

Fig. 4-13 : Circuit équivalent de supercondensateur à l'état initial (fin de charge à une tension constante)

Dans ce cas, la charge initiale Q0 emmagasinée dans la capacité C1 peut être calculée par la formule suivante :

Q₀ = C₁. U₀ 4-11

· Après l'état initial, la différence des tensions des deux capacités C et C , due à

1 rp

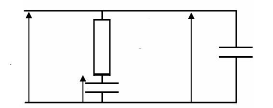
l'accumulation de charge près des interfaces des électrodes-électrolyte, conduit à diffuser une partie de la charge stockée Q0 dans la double couche (représentée par C1) vers les interfaces électrodes-électrolyte (représentées par _Crp). Le circuit à considérer est celui de la figure 4-14, bien entendu en négligeant l'effet du courant de fuite.

Rrp

Uc1=U0

Crp

UCrp = 0

U0

C1

Fig. 4-14 : Répartition des tensions des éléments du circuit à l'état initial

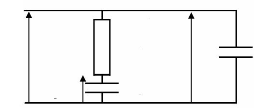
· A la fin de la période d'autodécharge par processus de diffusion lié à l'oxydoréduction, le courant de diffusion s'annule, les tensions des deux capacités C1 et _Crp sont égales et valent la tension aux bornes du supercondensateur _Urf. La charge totale Q_r stockée est égale la charge initiale Q0.

Rrp

Uc1 =Urf

Crp

UCrp =Urf

Urf

C1

Fig. 4-15 : Répartition des tensions sur les éléments du circuit
à la fin de la phase du processus de diffusion lié à l'oxydoréduction

Nous pouvons donc écrire les équations suivantes :

Q_r = Q₀ = U0 . C₁( U 0) 4-12

Q r = Urf.( C1 (Urf )+C_rp) 4-13

où,

Urf est la tension aux bornes du supercondensateur à la fin de la période de l'autodécharge du processus de diffusion lié à l'oxydoréduction.

Nous pouvons donc écrire :

C₁ ( U₀). U₀ -C₁ ( U,f ) U_rf )

C = 4-14

rp

Urf

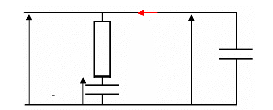
Par ailleurs, à partir de la figure ci-dessous (cf. fig. 4-16), nous pouvons écrire les équations suivantes :

u ( t ) = i (t ) .R _rp + u _crp (t)

du t

( ) 4-15

rp du t

( )

i t C

( ) = = - 1

C

rp

dt dt

u(t)

C1

uc1(t)

Crp

Rrp

i (t)

uCrp(t)

Fig. 4-16 : Circuit équivalent du supercondensateur lors de l'autodécharge
du processu s de diffusion lié à l'oxydoréduction

D'où, nous pouvons déduire l'équation différentielle suivante :

d u t C + C rp du t

2 ( ) 1 ( )

C R = 0 4-16

1 rp dt 2 + C dt

rp

La résolution de cette équation avec la condition initiale présentée précédemment permet de

calculer la tension instantanée aux bornes

du supercondensateur pendant la durée de

l'autodécharge par processus de diffusion lié à l'oxydoréduction par la fonction exponentielle suivante :

??

u t U

( ) 0 exp ??- t

= 4-17

? r ?

ô

avec,

U0 la tension initiale aux bornes du supercondensateur,

T_r la constante du temps de la charge de la capacité C_rp, qui peut être calculée par l'équation suivante :

C C R 1

rp rp

4. Etude, caractérisation et modélisation de l'autodécharge des supercondensateurs

ô = 4-18

r C C

+

1 rp

En supposant que la capacité C1 _>>Crp la constante du temps peut être donc réduite comme suit :

ô r = C _rp R rp 4-19

La résistance _Rrp, qui représente l'évolution des réactions faradiques aux interfaces électrodesélectrolyte, peut être calculée par l'équation suivante :

ô r

R = 4-20

^rp C

rp

Crp (kF)	Rrp (?)		Rf (k?)	0,2
85	1,34

Tab. 4-2 : Valeurs des éléments du circuit parallèle de l'autod arge

éch

pour le supercondensateur BCAP010

La comparaison entre la simulation des modèles réalisés avec les résultats expérimentaux, effectuée sur la figure 4-17, montre que le modèle du circuit parallèle est aussi précis que les autres modèles : analytique et circuit série (erreur relative moyenne de 1,2%).

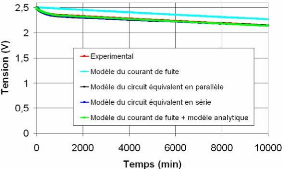
Fig. 4-17 : Comparaison de la simulation du circuit parallèle de l'autodécharge
avec la courbe expérimentale et les autres modèles réalisés

En fait, la valeur de la résistance _Rrp peut augmenter avec le temps ainsi que la résistance de fuite Rf, selon l'état thermodynamique de supercondensateur, ralentissant ainsi la charge dans

la capacité _Crp. Malgré cela, ce modèle montre qu'une partie de la charge de la capacité Crp peut se décharger dans la résistance de fuite Rf en tenant compte de l'effet de navette.